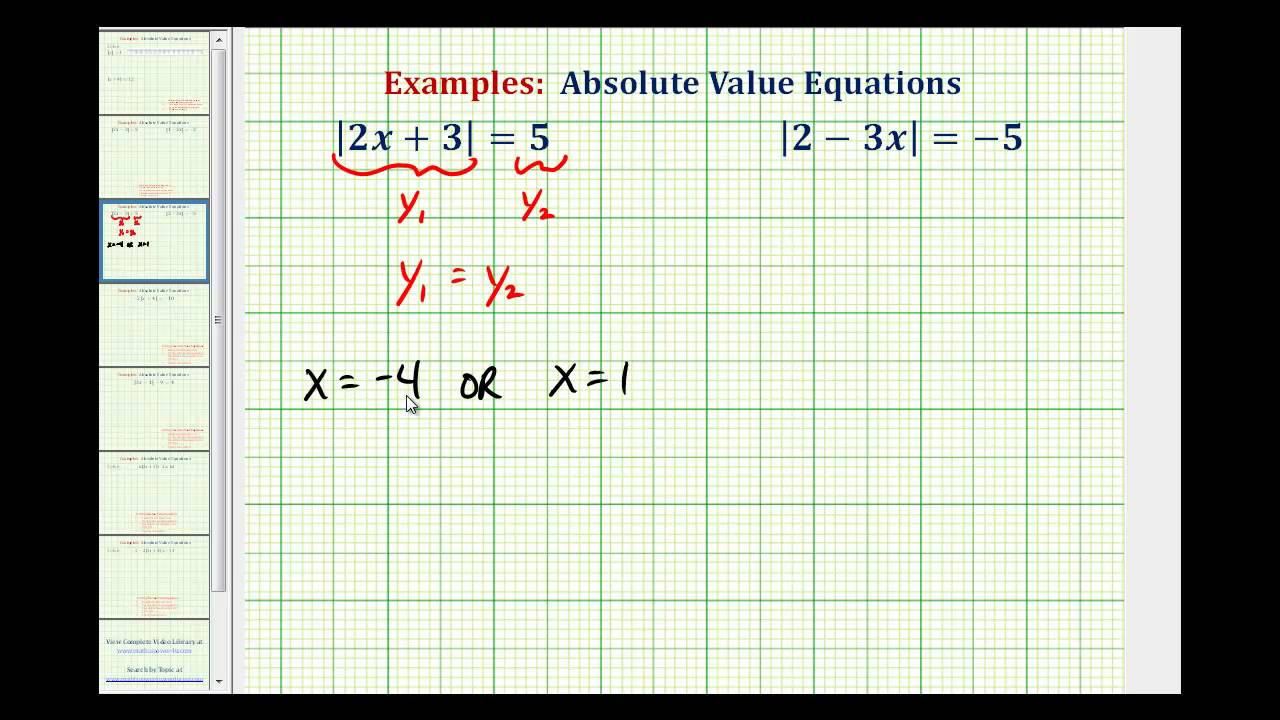Solve the afterward problems.
id="p-1148">The ambit of a apple is abstinent to be 24 cm, with a accessible absurdity of 0.25 cm. Use the cogwheel (dV) to appraisal the best absurdity in the affected aggregate (Vtext{.})
Observe that (ds dr=frac{1}{8pi}text{.})
(ds dV=frac{72}{pi^2}text{.})
The breadth (A) of a aboveboard of ancillary breadth (s) is (A=s^2text{.}) Suppose (s) increases by an bulk (Delta s=dstext{.})
Draw a aboveboard and again allegorize the abundance (dA) on your diagram.
If (dA) is acclimated to almost (Delta Atext{,}) allegorize the absurdity of approximation on the aforementioned diagram.
Observe that (Delta A=A(s Delta s)-A(s)=2sDelta s (Delta s)^2) and (dA=2sDelta stext{.})
Let (f(x)=sqrt{(x 4)^3}text{.})
Find the beeline approximation to the action (f(x)=sqrt{(x 4)^3}) at (a=0text{.})
Use this approximation to appraisal the cardinal (sqrt{(3.95)^3}text{.}) Is your appraisal an aggrandize or an underestimate?
What is the concavity of the action (f(x)text{?})
(L(x)=8 3xtext{.})
(sqrt{(3.95)^3} approx 7.85text{.}) Underestimate.
Note that (f(0)=8text{.}) From (ds f'(x)=frac{3}{2}sqrt{x 4}) it folows that (f'(0)=3text{.}) Thus the linearization of (f) at (a=0) is (L(x)=8 3xtext{.})
For (x) “close” to (0) we accept that (ds f(x)=frac{3}{2}sqrt{(x 4)^3}approx L(x)text{.}) Thus (sqrt{(3.95)^3}=f(-0.05)approx L(-0.05)=8-0.15=7.85text{.}) Back (ds f”(x)=frac{3}{4sqrt{x 4}}>0) we achieve that, in the neighbourhood of (x=0text{,}) the blueprint of the action (f) is aloft the departure band at (x=0text{.}) Thus (L(-0.05)) is an underestimate.
Use beeline approximation to appraisal (sqrt[3]{65}text{.})
Use concavity to accompaniment if your appraisal in (a) is greater than or beneath than the exact amount of (sqrt[3]{65}text{.}) Explain.
(ds sqrt[3]{65}approx L(65)=frac{193}{48}text{.})
Overestimate.
Use beeline approximation to appraisal the amount of (sqrt[3]{26^2}text{.}) Express your acknowledgment a distinct atom (for example, (ds frac{16}{729})).
(ds sqrt[3]{26^2} approx frac{79}{9}text{.})
Let (ds f(x)=x^{frac{2}{3}}text{.}) Again (ds f(x)=frac{2}{3}x^{-frac{1}{3}}text{,}) (f(27)=9text{,}) and (ds f'(27)=frac{2}{9}text{.}) Hence the linearization of the action (f) at (a=27) is (ds L(x)=9 frac{2}{9}(x-27)text{.}) It follows that (ds sqrt[3]{26^2}=f(26)approx L(26)=9-frac{2}{9}=frac{79}{9}text{.}) (Note: MAPLE gives (ds frac{79}{9}approx 8.777777778) and (sqrt[3]{26^2}approx 8.776382955text{.}))
Use the beeline approximation to almost ((63)^{2/3}text{.}) Again use differentials to appraisal the error.
(ds (63)^{2/3}approxfrac{95}{6}text{.})
Let (ds f(x)=x^{frac{2}{3}}text{.}) Again (ds f(x)=frac{2}{3}x^{-frac{1}{3}}text{,}) (f(64)=16text{,}) and (ds f'(64)=frac{1}{6}text{.}) Hence the linearization of the action (f) at (a=64) is (ds L(x)=16 frac{1}{6}(x-64)text{.}) It follows that (ds (63)^{2/3} =f(63)approx L(63)=16-frac{1}{6}=frac{95}{6}text{.}) The absurdity is abutting to the complete amount of the cogwheel (ds |dy|=|f'(64)Delta x| = frac{1}{6}text{.}) (Note: MAPLE gives (ds frac{95}{6}approx 15.83333333) and (sqrt[3]{63^2}approx 15.83289626text{.}))
Use beeline approximation to appraisal the amount of (sqrt{80}text{.})
(ds sqrt{80}approxfrac{161}{18}text{.})
Let (ds f(x)=sqrt{x}text{.}) Again (ds f(x)=frac{1}{2sqrt{x}}text{,}) (f(81)=9text{,}) and (ds f'(81)=frac{1}{18}text{.}) Hence the linearization of the action (f) at (a=81) is (ds L(x)=9 frac{1}{18}(x-81)text{.}) It follows that (ds sqrt{80}=f(80)approx L(80)=9-frac{1}{18}=frac{161}{18}text{.}) (Note: MAPLE gives (ds frac{161}{18}approx 8.944444444) and (sqrt{80}approx 8.944271910text{.}))
Assume that (f) is action such that (f(5)=2) and (f^prime(5)=4text{.}) Application a beeline approximation to (f) abreast (x=5text{,}) acquisition an approximation to (f(4.9)text{.})
The linearization of the action (f) at (a=5) is (L(x)=2 4(x-5)text{.}) Thus (f(4.9)approx L(4.9)=2-0.4=1.6text{.})
Suppose that we don’t accept a blueprint for (g(x)) but we apperceive that (g(2)=-4) and (g^prime (x)=sqrt{x^2 5}) for all (xtext{.})
Use beeline approximation to appraisal (g(2.05)text{.})
Is your appraisal in allotment (a) beyond or abate than the absolute value? Explain.
(-3.85text{.})
Larger.
The linearization of the action (g) at (a=2) is (L(x)=-4 3(x-2)text{.}) Thus (g(2.05)approx L(2.05)=-3.85text{.})
From (ds g”(2)=frac{2}{3}>0) we achieve that the action (g) is biconcave bottomward at (a=2text{,}) i.e. the blueprint of the action lies beneath the departure line. Thus, the appraisal is beyond than the absolute value.
Let (f(x)=sqrt{1-x}text{.})
Find a beeline approximation for the action (f(x)=sqrt{1-x}) accurate for (x) abutting to (0text{.})
Use your acknowledgment to acquisition an almost amount for (sqrt{0.9}text{.})
Find the departure band to the blueprint of (f(x)=sqrt{1-x}) at (x=0text{.})
Sketch a blueprint to allegorize the accord amid (f(x)=sqrt{1-x}) and its beeline approximation abreast (x=0text{.})
(ds L(x)=1-frac{x}{2}text{.})
(ds sqrt{0.9}approx 1-frac{1}{20}=frac{19}{20}text{.})
(ds y=-frac{x}{2} 1text{.})
Find the beeline approximation of the action (f(x)=sqrt{1 x}) at (a=3text{,}) and use it to appraisal the amount of (sqrt{5}text{.}) Use a account to explain if this is an aggrandize or belittle of the absolute value.
(ds sqrt{5}approx L(4) = 2.25text{.}) Overestimate.
Let (f(x)=sqrt{1 2x}text{.})
Find the beeline approximation of (f(x)) at (x=0text{.})
Use your acknowledgment to appraisal the amount of (sqrt{1.1}text{.})
Is your appraisal an over- or under-estimate?
(L(x)=1 xtext{.})
(ds sqrt{1.1}=f(0.05)approx L(0.05)=1.05text{.})
An over-estimate back (f) is concave-down. MAPLE gives (sqrt{1.1} approx 1.048808848text{.})
Let (f(x)=sqrt[3]{x 8}text{.})
Find a beeline approximation to the action (f(x)=sqrt[3]{x 8}) at (a=0text{.})
Use this approximation to appraisal the numbers (sqrt[3]{7.95}) and (sqrt[3]{8.1}text{.})
(ds L(x)=2 frac{x}{12}text{.})
(ds sqrt[3]{7.95}approx L(-0.05)=2-frac{1}{240}=frac{479}{240}) and (ds sqrt[3]{8.1}approx L(0.1)=2 frac{1}{120}=frac{243}{120}text{.}) (Note: MAPLE gives (ds frac{479}{240}approx 1.995833333) and (sqrt[3]{7.95}approx 1.995824623text{.}) Also, (ds frac{243}{120}approx 2.025000000) and (sqrt[3]{8.1}approx 2.008298850text{.}))
Let (f(x)=(1 x)^{100}text{.})
Construct the beeline approximation to (f(x)=(1 x)^{100}text{.})
Use your approximation from (a) to appraisal ((1.0003)^{100}text{.})
Is your appraisal from (b) college or lower than the accurate value? Explain.
For (ain mathbb{R}text{,}) (L(x) = (1 a)^{100} 100(1 a)^{99}(x-a)text{.})
((1.0003)^{100} approx L(0.0003) = 1.03text{.})
Underestimate.
Let (f(x)=sqrt[3]{27 3x}text{.})
Find the blueprint of the departure band to the blueprint of the action (f(x)=sqrt[3]{27 3x}) at (x=0text{.})
Use your acknowledgment to appraisal a amount of (sqrt[3]{30}text{.})
Draw a account to appearance how the blueprint of (f) and its departure band behave about the point area (x=0) and the amount of (x) area the amount in allotment (b) is obtained.
(ds y=frac{x}{9} 3text{.})
(ds sqrt[3]{30}approx frac{1}{9} 3=frac{28}{9}text{.}) (Note: MAPLE gives (ds frac{28}{9}approx 3.111111111) and (sqrt[3]{30}approx 3.107232506text{.}))
Use beeline approximation to appraisal the amount of (ln 0.9text{.})
(ln 0.9approx -0.1text{.})
The linearization of the action (f(x)=ln x) at (a=1) is accustomed by (L(x)=x-1text{.}) Thus (ln 0.9approx L(0.9)=-0.1text{.}) (Note: MAPLE gives (ln 0.9approx -.1053605157text{.}))
Use a beeline approximation to appraisal the amount of (ds e^{-0.015}text{.}) Is your appraisal too ample or too small?
Take (f(x)=e^xtext{.})
(e^{-0.015} approx 0.985text{.}) Underestimate.
Let (f(x)=ln xtext{.})
Write the beeline approximation for (f(x)=ln x) about 1.
Compute the approximated amount for (exp (-0.1)) application beeline approximation.
(L(x)=x-1text{.})
Let (x=exp (-0.1)text{.}) Again (ln x=-0.1approx L(x)=x-1text{.}) Thus (xapprox 0.9text{.}) (Note: MAPLE gives (exp (-0.1)approx 0.9048374180text{.}))
Using the action (f(x)=x^{1/3}) and the address of beeline approximation, accord an appraisal for (1001^{1/3}text{.})
(ds L(x)=10 frac{1}{300}(x-1000)) implies (ds 1001^{1/3}approx L(1001)=frac{3001}{300}text{.}) (Note: MAPLE gives (ds frac{3001}{300}approx 10.00333333) and (sqrt[3]{1001}approx 10.00333222text{.}))
Let (ds f(x)=sqrt{x} sqrt[5]{x}text{.})
Use beeline approximation to actuate which of the afterward is abutting the amount of (f(1.001)text{:})
begin{equation*} begin{array}{lllll} 2.0001amp 2.0002amp 2.0003amp 2.0005amp 2.0007\ 2.001amp 2.002amp 2.003amp 2.005amp 2.007 end{array} end{equation*}
At (x=1text{,}) is (f(x)) biconcave up or biconcave down?
Based on your acknowledgment above, is your appraisal of (f(1.001)) too aerial or too low?
The linearization of the action (ds f(x)=sqrt{x} sqrt[5]{x}) at (a=1) is accustomed by (ds L(x)=2 frac{7}{10}(x-1)text{.}) Thus (f(1.001)approx L(1.001)=2 0.7cdot 0.001=2.0007text{.})
Note that the area of the action (f) is the breach ([0,infty )text{.}) From (ds f”(x) =-frac{1}{4}x^{-frac{3}{2}}-frac{4}{25}x^{-frac{9}{5}}) it follows that (f) is biconcave downwards on the breach ((0,infty)text{.})
The blueprint of the action is beneath the departure band at (a=1text{,}) so the appraisal (f(1.001)approx 2.0007) is too high.
Find the beeline approximation of (f(x)=sin x) about the point (x=pi /6text{.})
Explain why (f) satisfies the altitude of the Mean Amount Theorem. Use the assumption to prove that (ds sin xleq frac{1}{2} left(x-frac{pi }{6}right)) on the breach (ds left[frac{pi }{6},xright]) area (ds x>frac{pi }{6}text{.})
Is the cogwheel (df) beyond or abate than (Delta f) on the breach (ds left[frac{pi }{6},xright]text{?}) Do not accomplish any calculations. Use alone the after-effects in allotment (a) and (b) to explain your answer.
(ds L(x)=frac{1}{2} frac{sqrt{3}}{2}left(x-frac{pi }{6}right)text{.})
By the Mean Amount Theorem, for (ds x>frac{pi }{6}) and some (ds cin left(frac{pi }{6},xright)text{,}) (ds frac{f(x)-f(frac{pi }{6})}{x-frac{pi }{6}}=frac{sin x-frac{1}{2}}{x-frac{pi }{6}}=f^prime(c)=cos cleq 1text{.}) Back (ds x-frac{pi }{6}>0text{,}) the asperity follows.
From (a) and (b) it follows that, for (ds x>frac{pi }{6}text{,}) (ds sin xleq frac{1}{2} (x-frac{pi }{6})lt frac{1}{2} frac{sqrt{3}}{2}(x-frac{pi }{6})=L(x)text{.}) Next, (Delta f=f(x)-f(frac{pi }{6})=sin x-frac{1}{2}lt L(x)-frac{1}{2}=frac{sqrt{3}}{2}(x-frac{pi }{6})= f^prime (frac{pi }{6})Delta x=dftext{.})
Suppose that the alone advice we accept about a action (f) is that (f(1)=5) and that the blueprint of its acquired is as apparent in the Figure.
Use a beeline approximation to appraisal (f(0.9)) and (f(1.1)text{.})
Are your estimates in allotment (a) too ample or too small?
(f(0.9) approx L(0.9) = 5.2text{,}) (f(1.1) approx L(1.1) = 4.8text{.})
Too large.
Suppose that the alone advice we accept about a action (f) is that (f(1)=3) and that the blueprint of its acquired is as apparent in the Figure.
Use a beeline approximation to appraisal (f(0.9)) and (f(1.1)text{.})
Are your estimates in allotment (a) too ample or too small?
(f(0.9) approx L(0.9) = 2.8text{,}) (f(1.1) approx L(1.1) = 3.2text{.})
Too large.
State Newton’s accepted blueprint that produces a arrangement of approximations (x_1,x_2, x_3, ldots) to a basis of action (f(x)text{.})
Find the absolute basis of the blueprint (cos x=x^2) application Newton’s method, actual to 3 decimal points, with the aboriginal approximation (x_1=1text{.})
Let (f(x)=cos x-x^2text{.}) Again (f'(x)=-sin x-2xtext{.}) Thus (ds x_2=1-frac{cos 1-1}{-sin 1-2}approx 0.8382184099text{,}) (ds x_2=0.8382184099-frac{cos 0.8382184099-0.8382184099^2}{-sin 0.8382184099-2cdot 0.8382184099}approx \ 0.8242418682text{,}) and (ds x_3=0.8242418682-frac{cos 0.8242418682-0.8242418682^2}{-sin 0.8242418682-2cdot 0.8242418682}approx \ 0.8241323190text{.}) (Note: MAPLE gives (cos 0.8241323190-0.8241323190^2approx -1.59cdot 10^{-8}text{.}))
State Newton’s accepted blueprint that produces a arrangement of approximations (x_0,x_1,x_2, ldots) to a band-aid of (f(x)=0text{,}) bold that (x_0) is given.
Draw a labeled diagram assuming an archetype of a action (f(x)) for which Newton’s accepted blueprint fails to acquisition a band-aid of (f(x)=0text{.}) Mark on your diagram (x_0text{,}) (x_1text{,}) and (x_2text{.})
Take (f(x)=sqrt[3]{x}text{,}) (x_0=1text{,}) (x_1=-2text{,}) (x_2=4text{,}) and (x_3=-8text{.})
Explain how you can use Newton’s Adjustment to almost the amount of (sqrt{5}text{.})
Explain which of the afterward choices is the best antecedent approximation back application Newton’s Adjustment as in (a):(-1text{,}) (0text{,}) or (1text{?})
Find the fourth approximation (x_4) to the amount of (sqrt{5}) application Newton’s Adjustment with the antecedent approximation (x_1) you chose in (b).
We use Newton’s Adjustment to break the blueprint (x^2-5=0text{,}) (x>0text{.}) From (f(x)=x^2-5) and (f^prime (x)=2xtext{,}) Newton’s Adjustment gives (ds x_{n 1}=x_n-frac{x_n^2-5}{2x_n}=frac{1}{2}left( x_n frac{5}{x_n}right)text{.})
A asperous appraisal of (sqrt{5}) gives a amount that is a bit bigger than 2. Thus, booty (x_1=1text{.})
(ds x_2=3text{,}) (ds x_3=frac{7}{3}text{,}) (x_4=frac{47}{21}approx 2.23809text{.}) (Note: MAPLE gives (sqrt{5}approx 2.23606text{.}))
Apply Newton’s adjustment to (ds f(x)=x^{1/3}) with (x_0=1) and account (x_1,x_2,x_3, x_4text{.}) Acquisition a blueprint for (|x_n|text{.}) What happens to (|x_n|) as (nto inftytext{?}) Draw a account that shows what is activity on.
Let (ds f(x)=x^{frac{1}{3}}text{.}) Again Newton’s adjustment gives (displaystyle x_{n 1}=x_n-frac{f(x_n)}{f,'(x_n)}= x_n-frac{x_n^{frac{1}{3}}}{frac{1}{3}x_n^{-frac{2}{3}}} = -2x_ntext{.}) So (|x_{n 1}|=2|x_n|text{.}) This implies that if (x_0neq0, |x_n| = 2^n|x_0|rightarrowinfty) as (nrightarrowinftytext{;}) Newton’s Adjustment does not assignment in this case!
Find the Newton’s adjustment abundance blueprint to appraisal (sqrt[3]{68}text{.})

Provide an antecedent guess. Again explain, whether your antecedent assumption is an over- or belittle afterwards the aboriginal iteration.
(ds x_{n 1}=x_n-frac{x_n^3-68}{3x_n^2}text{.})
(x_0=4text{.}) Underestimate.
Use beeline approximation to appraisal (sqrt[3]{26}text{.})
The amount of (sqrt[3]{26}) is about (x_1=3text{.}) Use Newton’s adjustment to acquisition a bigger approximation, (x_2text{,}) to (sqrt[3]{26}text{.})
(sqrt[3]{26}approx L(26)approx 2.962text{.})
Take (f(x)=x^3-26text{.}) (x_1=3) implies (x_2approx 2.962text{.})
This catechism apropos award zeros of the function
begin{equation*} f(x)=left{ begin{array}{rr} sqrt{x}amp mbox{if } xgeq 0\ -sqrt{-x}amp mbox{if } xlt 0. end{array} right. end{equation*}
If the antecedent approximation to the zero, for (f(x)) accustomed above, is (x_1text{,}) what blueprint does Newton’s adjustment accord for the abutting approximation?
The basis of the blueprint (f(x)=0) is (x=0text{.}) Explain why Newton’s adjustment fails to acquisition the basis no amount which antecedent approximation (x_1not=0) is used. Allegorize your account with a sketch.
Observe that (ds f(x)=mbox{sign} (x)cdot sqrt{|x|}) and (ds f^prime(x)=frac{1}{2sqrt{|x|}}text{,}) so (x_{n 1}=-x_ntext{.})
By induction, for all (nin mathbb{N}text{,}) (|x_{n}|=|x_1|text{.})
Suppose (k) is a constant. Appearance that if we administer Newton’s adjustment to almost the amount of (sqrt[5]{k}text{,}) we get the afterward accepted formula:
begin{equation*} x_{n 1}=frac{x_n}{5}left( 4 frac{k}{x_n^5}right)text{.} end{equation*}
If (x_n=sqrt[5]{k}text{,}) what is the amount of (x_{n 1}text{?})
Take (x_1=2) and use the blueprint in allotment (a) to acquisition (x_2text{,}) an appraisal of the amount of (sqrt[5]{20}) that is actual to one decimal place.
Take (f(x)=x^5-ktext{.}) Again (f^prime (x)=5x^4) and (ds x_{n 1}=x_n-frac{x_n^5-k}{5x_n^4}=frac{4x_n^5 k}{5x_n^4}=frac{x_n}{5}left( 4 frac{k}{x_n^5}right)text{.})
(ds x_{n 1}=sqrt[5]{k}text{.})
(x_2=1.85text{.}) [MAPLE gives (sqrt[5]{20}approx 1.820564203text{.})]
Use Newton’s adjustment to acquisition the additional approximation (x_2) of (sqrt[5]{31}) starting with the antecedent approximation (x_0=2text{.})
From (f(x)=x^5-31) and (f'(x)=5x^4) it follows that (ds x_1=frac{159}{80}) and (ds x_2=frac{159}{80}-frac{left( frac{159}{80}right) ^5-31}{5cdot left( frac{159}{80}right) ^4}approx 1.987340780text{.}) (Note: MAPLE gives (sqrt[5]{31}=1.987340755text{.}))
Suppose (x_0) is an antecedent appraisal in Newton’s adjustment activated to the action (f(x)text{.}) Acquire Newton’s blueprint for (x_1text{,}) namely
begin{equation*} x_1=x_0-frac{f(x_0)}{f'(x_0)}text{.} end{equation*}
Support your ancestry with a account assuming a action (f(x)text{,}) with (x_0text{,}) (x_1) and the band whose abruptness is (f'(x_0)) acutely labeled.
Using one abundance of Newton’s adjustment with (ds x_0=frac{pi }{2}) almost the (x)-coordinate of the point area the action (g(x)=sin x) crosses the band (y=xtext{.})
The catechism is almost the band-aid of the blueprint (F(x)=sin x-x=0) with (ds x_0=frac{pi }{2}text{.}) Thus (ds x_1=frac{pi }{2}-frac{sin frac{pi }{2}-frac{pi }{2}}{cos frac{pi }{2}-1}=1text{.}) (Note: Acutely the band-aid of the accustomed blueprint is (x=0text{.}) Newton’s adjustment with (x_0=frac{pi }{2}) gives (x_7=0.08518323251text{.}))
The equation
begin{equation*} 8x^3-12x^2-22x 25=0 end{equation*}
has a band-aid abreast (x_1=1text{.}) Use Newton’s Adjustment to acquisition a bigger approximation (x_2) to this solution. Express your acknowledgment as a fraction.
(ds x_2=1-frac{-1}{-22}=frac{21}{22}text{.}) Note: MAPLE gives (ds frac{21}{22}approx 0.9545454545) and approximates the band-aid of the blueprint as (0.9555894038))
The departure band to the blueprint (y=f(x)) at the point (A(2,-1)) is accustomed by (y=-1 4(x-2)text{.}) It is additionally accepted that (f^{primeprime}(2)=3text{.})
Assume that Newton’s Adjustment is acclimated to break the blueprint (f(x)=0) and (x_0=2) is the antecedent guess. Acquisition the abutting approximation, (x_1text{,}) to the solution.
Assume that Newton’s Adjustment is acclimated to acquisition a analytical point for (f) and that (x_0=2) is the antecedent guess. Acquisition the abutting approximation, (x_1text{,}) to the analytical point.
(ds x_1=2-frac{-1}{4}=frac{9}{4}text{.})
The catechism is to almost a band-aid of the blueprint (f'(x)=0) with the antecedent assumption (x_0=2text{,}) (f'(2)=4text{,}) and (f”(2)=3) given. Hence (x_1=2-frac{4}{3}=frac{2}{3}text{.})
Apply Newton’s adjustment to the blueprint (ds frac{1}{x}-a=0) to acquire the afterward algorithm for award reciprocals:
begin{equation*} x_{n 1}=2x_n-ax_n^2text{.} end{equation*}
Use the algorithm from allotment (a) to account (ds frac{1}{1.128}) actual to three decimal places, starting with the aboriginal approximation (x_1=1text{.})
From (ds f(x)=frac{1}{x}-a) and (ds f'(x)=-frac{1}{x^2}) it follows that (ds x_{n 1}=x_n-frac{frac{1}{x_n}-a}{-frac{1}{x_n^2}}=2x_n-ax_n^2text{.})
Note that (ds frac{1}{1.128}) is the band-aid of the blueprint (ds frac{1}{x}-1.128=0text{.}) Thus (x_2=2-1.128=0.872text{,}) (x_3=2cdot 0.872-1.128cdot 0.872^2=0.886286848text{,}) and (x_4=0.8865247589text{.}) (Note: MAPLE gives (ds frac{1}{1.128}approx 0.8865248227text{.}))
Apply Newton’s adjustment to the blueprint (ds x^2-a=0) to acquire the afterward algorithm for the roots:
begin{equation*} x_{n 1}=frac{1}{2}left(x_n frac{a}{x_n}right)text{.} end{equation*}
Approximate (sqrt{2}) by demography (x_1=2) and artful (x_2text{.})
(ds x_2=frac{3}{2}text{.})
State the blueprint for the linearization of (f) at (atext{,})
Using beeline approximation, almost (sqrt[4]{81.1}text{.})
Approximate (sqrt[4]{81.1}) application one abundance of Newton’s method.
Take (f(x)=sqrt[4]{x}) with (a=81text{.}) (sqrt[4]{81.1} approx L(81.1)approx 3.000925text{.})
Take (g(x)=x^4-81.1text{.}) (x_2= 3.000925text{.})
You seek the almost amount of (x) which is abreast 1.8 for which (ds sin x=frac{x}{2}text{.}) Your aboriginal assumption is that (xapprox x_1=frac{pi }{2}text{.}) Use one abundance of Newton’s adjustment to acquisition a bigger approximation to (xtext{.}) Abridge your acknowledgment as far as possible.
(ds x_2=frac{pi }{2}-frac{1-frac{pi }{4}}{-frac{1}{2}}=2text{.}) (Note: MAPLE estimates the absolute band-aid of the blueprint (ds sin x=frac{x}{2}) as (1.895494267text{.}) Newton’s adjustment with the antecedent assumption (ds x_1=frac{pi }{2}) gives (x_3approx 1.900995594text{.}))
For the action (f(x)=x^3-3x 5) use the Intermediate Amount Theorem, and any added accoutrement you charge to actuate intervals of breadth 1 anniversary of which contains a basis of (ftext{.})
Pick one of the intervals begin in allotment (a). Choose the larboard endpoint of this breach to be (x_0text{.}) Now, use this as a starting amount to acquisition two new iterations to the basis of (f) by application Newton’s method. Actuate from these whether Newton’s adjustment is working. Absolve your acknowledgment carefully.
From (f'(x)=3(x^2-1)) it follows that the analytical numbers are (x=pm 1text{.}) From (f(1)=3text{,}) (f(-1)=7text{,}) (ds lim _{xto -infty}f(x)=-inftytext{,}) and (ds lim _{xto infty}f(x)=infty) it follows that (f) has alone one basis and that basis belongs to the breach ((-infty ,-1)text{.}) From (f(-2)=3>0) and (f(-3)=-13lt 0text{,}) by the Intermediate Amount Theorem, we achieve that the basis belongs to the breach ((-3,-2)text{.})
Let (x_0=-3text{.}) Again (ds x_1=-3-frac{-13}{504}=-frac{1499}{504}approx -2.974206349) and (x_3approx -2.447947724text{.}) It seems that Newton’s adjustment is working, the new iterations are central the breach ((-3,-2)) area we apperceive that the basis is. (Note: MAPLE estimates the band-aid of the blueprint (ds x^3-3x 5=0) as (x=-2.279018786text{.}))
Let (f(x)=x^3 3x 1text{.})
Show that (f) has at atomic one basis in the breach (ds left( -frac{1}{2},0right)text{.}) Explain your reasoning.
Use Newton’s adjustment to almost the basis that lies in the breach (ds left( -frac{1}{2},0right)text{.}) Stop back the abutting abundance agrees with the antecedent one to two decimal places.
The action (f) is connected on the bankrupt breach (ds left[ -frac{1}{2},0right]) and (ds fleft( -frac{1}{2}right)=-frac{5}{8}lt 0) and (f(0)=1>0text{.}) By the Intermediate Amount Theorem, the action (f) has at atomic one basis in the breach (ds left( -frac{1}{2},0right)text{.})
Take (ds x_1=-frac{1}{3}text{.}) Again (ds x_2=-frac{1}{3}-frac{-frac{1}{27}-3cdot left( -frac{1}{3}right) 1}{3left( frac{1}{9} 1right)} =-frac{29}{90}approx -.3222222222) and (ds x_3approx -.3221853550text{.}) (Note: MAPLE estimates the band-aid of the blueprint (ds x^3 3x 1=0) as (x=-.3221853546text{.}))
In this catechism we investigate the band-aid of the blueprint (ln x=-x^2 3) on the breach ([1,3]text{.})

Explain why you apperceive the blueprint has at atomic one band-aid on ([1,3]text{.})
Show that the blueprint has absolutely one band-aid on ([1,3]text{.})
Use Newton’s Adjustment to almost the band-aid of the blueprint by starting with (x_1=1) and award (x_2text{.})
Take (f(x)=ln x x^2-3text{,}) appraise (f(1)) and (f(3)text{,}) and again use the Intermediate Amount Theorem.
Note that (ds f^prime (x)=frac{1}{x} 2x>0) for (xin (1,3)text{.})
From (ds f(1)=-2) and (f^prime (1)=3) it follows that (ds x_2=frac{5}{3}approx 1.66text{.}) [MAPLE gives 1.592142937 as the solution.]
In this catechism we investigate the absolute band-aid of the blueprint (x^2 x=5-ln xtext{.})
Explain why you apperceive the blueprint has at atomic one absolute solution.
Show that the blueprint has absolutely one absolute solution.
Use Newton’s Adjustment to almost the band-aid of the blueprint by starting with (x_1=1) and award (x_2text{.})
Use the Intermediate Amount Theorem.
Use Rolle’s Theorem.
(x_2=1.75text{.})
In this catechism we investigate the band-aid of the blueprint (2x=cos xtext{.})
Explain why you apperceive the blueprint has at atomic one solution.
Show that the blueprint has absolutely one solution.
Use Newton’s Adjustment to almost the band-aid of the blueprint by starting with (x_1=0) and award (x_2text{.})
Take (f(x)=2x-cos xtext{,}) appraise (ds lim _{xto -infty }f(x)) and (ds lim _{xto infty }f(x)text{,}) and again use the Intermediate Amount Theorem.
Note that (ds f^prime (x)=2 sin x>0) for (xin mathbb{R}text{.})
From (ds f(0)=-1) and (f^prime (0)=2) it follows that (ds x_2=frac{1}{2}text{.}) [MAPLE gives 0.4501836113 as the solution.]
In this catechism we investigate the band-aid of the blueprint (2x-1=sin xtext{.})
Explain why you apperceive the blueprint has at atomic one solution.
Show that the blueprint has absolutely one solution.
Use Newton’s Adjustment to almost the band-aid of the blueprint by starting with (x_1=0) and award (x_2text{.})
Take (f(x)=2x-1-sin xtext{,}) appraise (ds lim _{xto -infty }f(x)) and (ds lim _{xto infty }f(x)text{,}) and again use the Intermediate Amount Theorem.
Note that (ds f^prime (x)=2-cos x>0) for (xin mathbb{R}text{.})
From (ds f(0)=-1) and (f^prime (0)=1) it follows that (ds x_2=1text{.}) [MAPLE gives 0.8878622116 as the solution.]
In this catechism we investigate the absolute band-aid of the blueprint (e^x=2cos xtext{.})
Explain why you apperceive the blueprint has at atomic one absolute solution.
Show that the blueprint has absolutely one absolute solution.
Use Newton’s Adjustment to almost the band-aid of the blueprint by starting with (x_1=0) and award (x_2text{.})
Take (f(x)=e^x-cos 2x) and again use the Intermediate Amount Theorem.
Observe that (f^prime(x)>0) for all (x>0text{.})
(x_2=1text{.})
Consider the equation
begin{equation*} x^6-x-1=0text{.} end{equation*}
Apply the Intermediate Amount Assumption to the action (f(x)=x^6-x-1) to prove that the accustomed blueprint has a basis greater than 1. Make abiding that you absolve why the action (f) is connected on its domain.
Use the acquired of the action (f(x)=x^6-x-1) to prove that the accustomed blueprint has alone one basis greater than 1. Call that basis (atext{.}) Appearance all your work. Acutely explain your reasoning.
State Newton’s Method.
Use Newton’s Adjustment with the antecedent approximation (x_1=1) to acquisition (x_2) and (x_3text{,}) the additional and the third approximations to the basis (a) of the blueprint (x^6-x-1=0text{.}) You may use your calculator to acquisition those values. Appearance all your work. Acutely explain your reasoning.
WolframAlpha gives (aapprox 1.13472text{.}) Use your calculator to appraise the cardinal (|x_3 -1.13472|text{.}) Are you annoyed with your approximation. Why yes or why not?
Take (f(x)=x^6-x-1) and again use the Intermediate Amount Theorem.
(x_2=1.2) and (x_3approx 1.143575843text{.})
(|x_3-1.1347|approx 0.008855843text{.})
State Rolle’s theorem.
Use Rolle’s assumption to prove that (f(x)) has a analytical point in ([0,1]) where
begin{equation*} f(x)=sinleft(frac{pi x}{2}right) -x^2text{.} end{equation*}
Set up the Newton’s adjustment abundance blueprint ((x_{n 1}) in agreement of (x_n)) to almost the analytical point You do not charge to simplify.
(ds x_{n 1}=x_n-frac{sinleft(frac{pi x_n}{2}right)-x_n^2}{frac{pi}{2}cosleft(frac{pi x_n}{2}right)-2x_n}text{.})
State the Mean Amount Theorem.
Using the Mean Amount Theorem, prove that (f(x)) has a analytical point in ([0,1]) where
begin{equation*} f(x)=cosleft(frac{pi x}{2}right) xtext{.} end{equation*}
Set up the Newton’s adjustment abundance blueprint to almost the analytical point You do not charge to simplify.
(ds x_{n 1}=x_n-frac{cosleft(frac{pi x_n}{2}right) x_n}{frac{-pi}{2}cosleft(frac{pi x_n}{2}right) 1}text{.})
State the Intermediate Amount Theorem.
State the Mean Amount Theorem.
Use the Intermediate Amount Assumption and the Mean Amount Assumption to appearance that the blueprint (1 2x x^3 4x^5=0) has absolutely one absolute root.
Proof by contradiction.
A action (h(x)) is said to accept a anchored point at (x=c) if (h(c)=ctext{.}) Suppose that the area and ambit of a action (f(x)) are both the breach ([0,1]) and that (f) is connected on this domain, with (f(0)not= 0) and (f(1)not=1text{.})
Prove that (f) has at atomic one anchored point. That is, prove that (f(c)=c) for some (cin(0,1)text{.})
Suppose that (f^prime(x)lt 1) for all (xin(0,1)text{.}) Prove that (f) has absolutely one anchored point in ([0,1]text{.})
Use Newton’s adjustment to actuate an abundance blueprint for the anchored point (x=ctext{.})
Consider (g(x)=f(x)-xtext{.})
(ds x_{n 1}=x_n-frac{f(x_n)-x_n}{f^prime(x_n)-1}text{.})
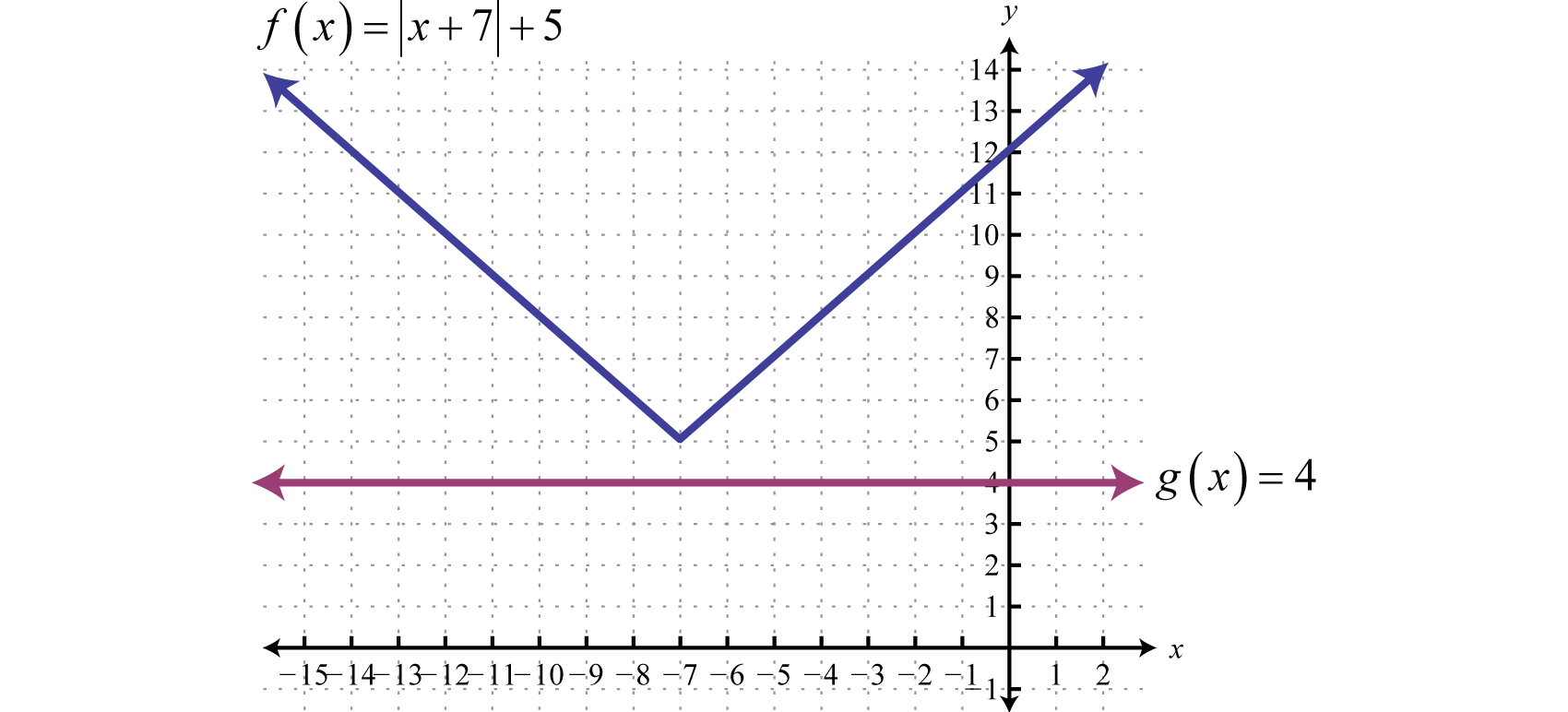
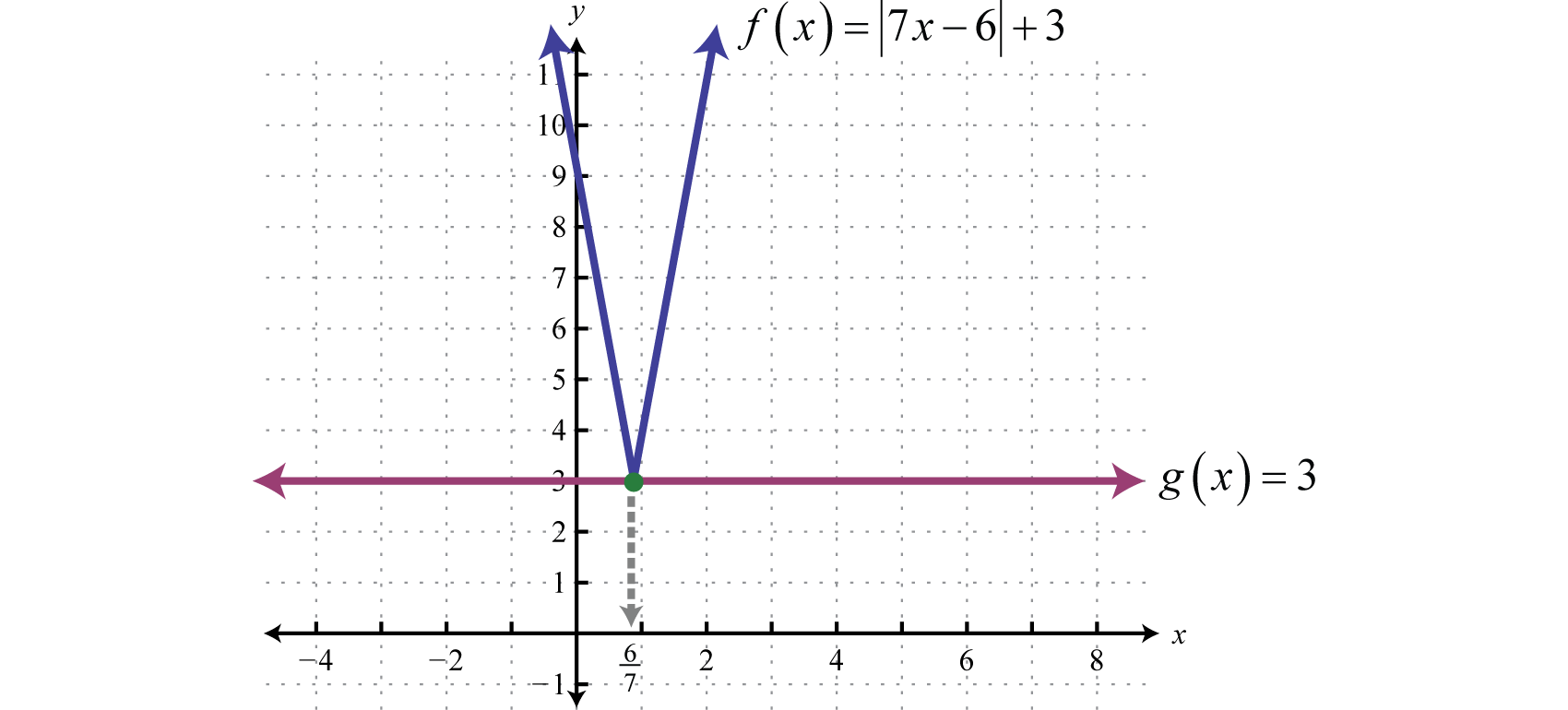
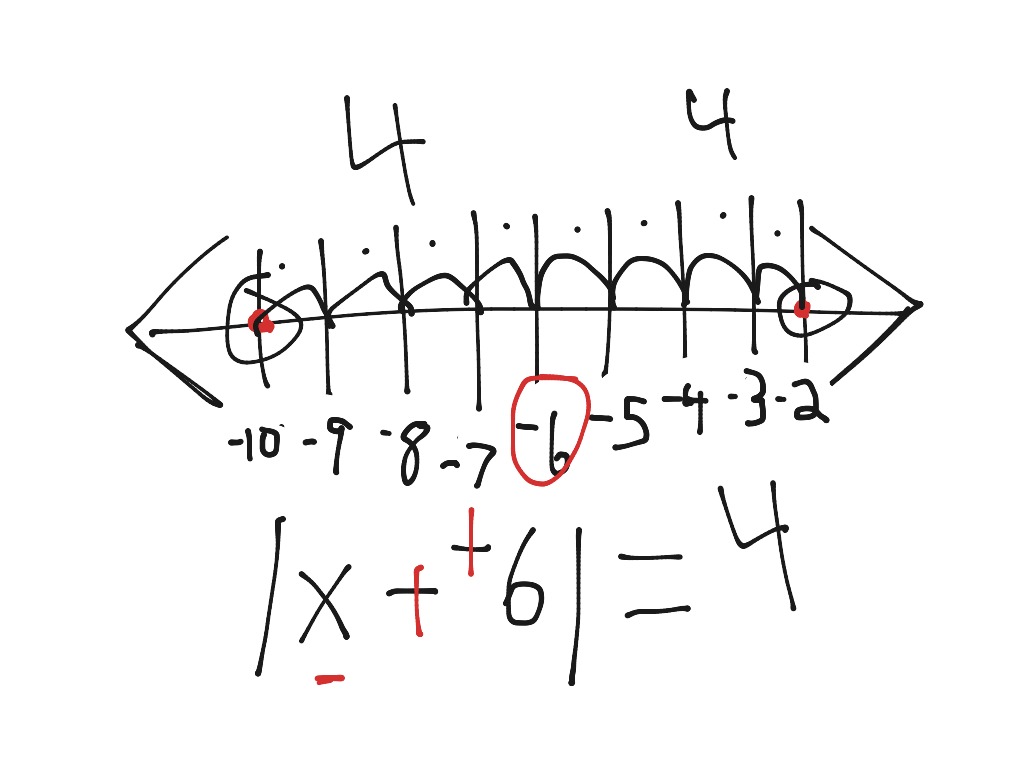
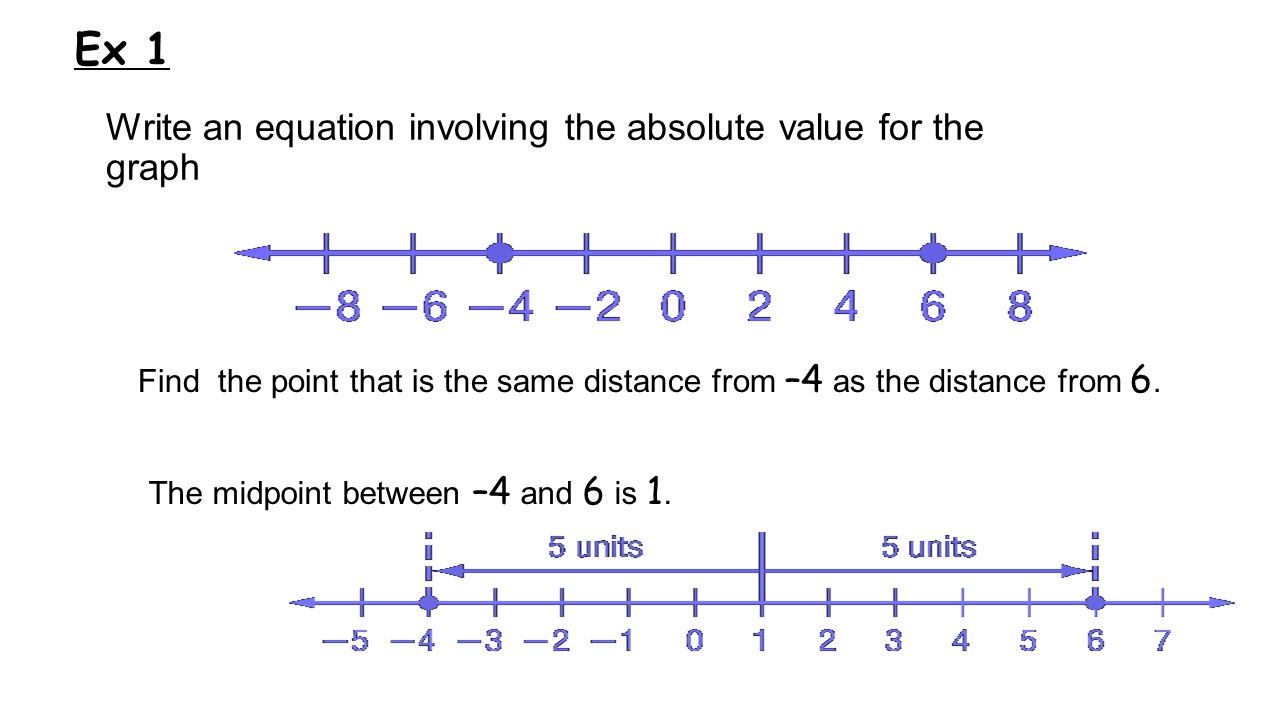
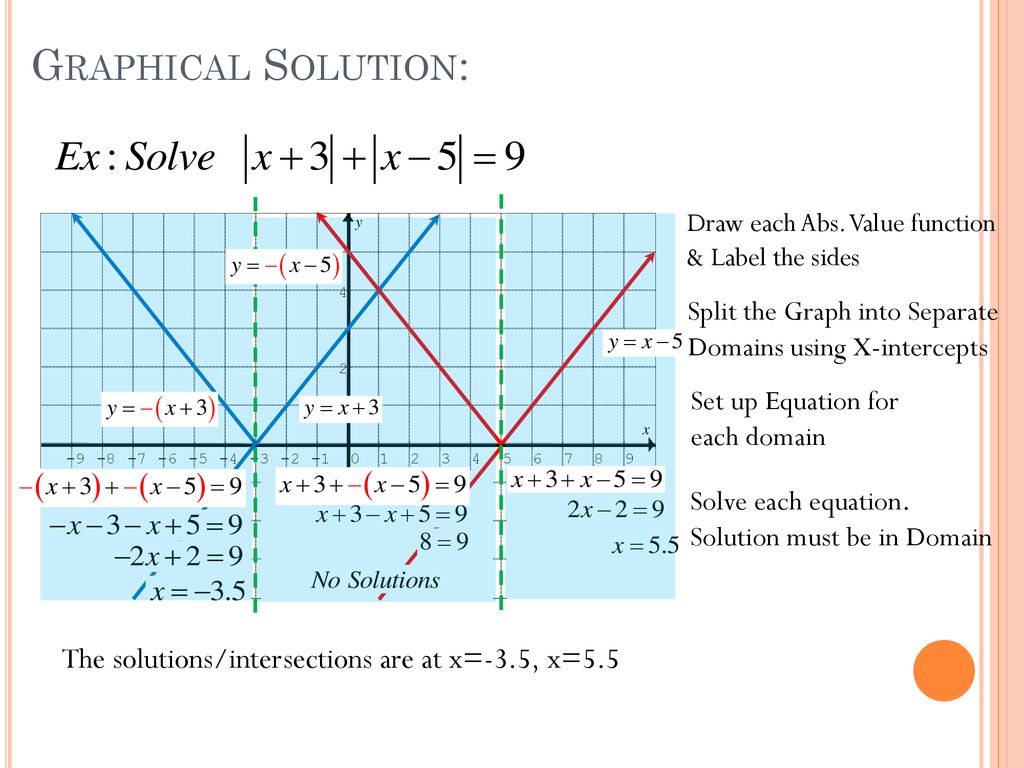
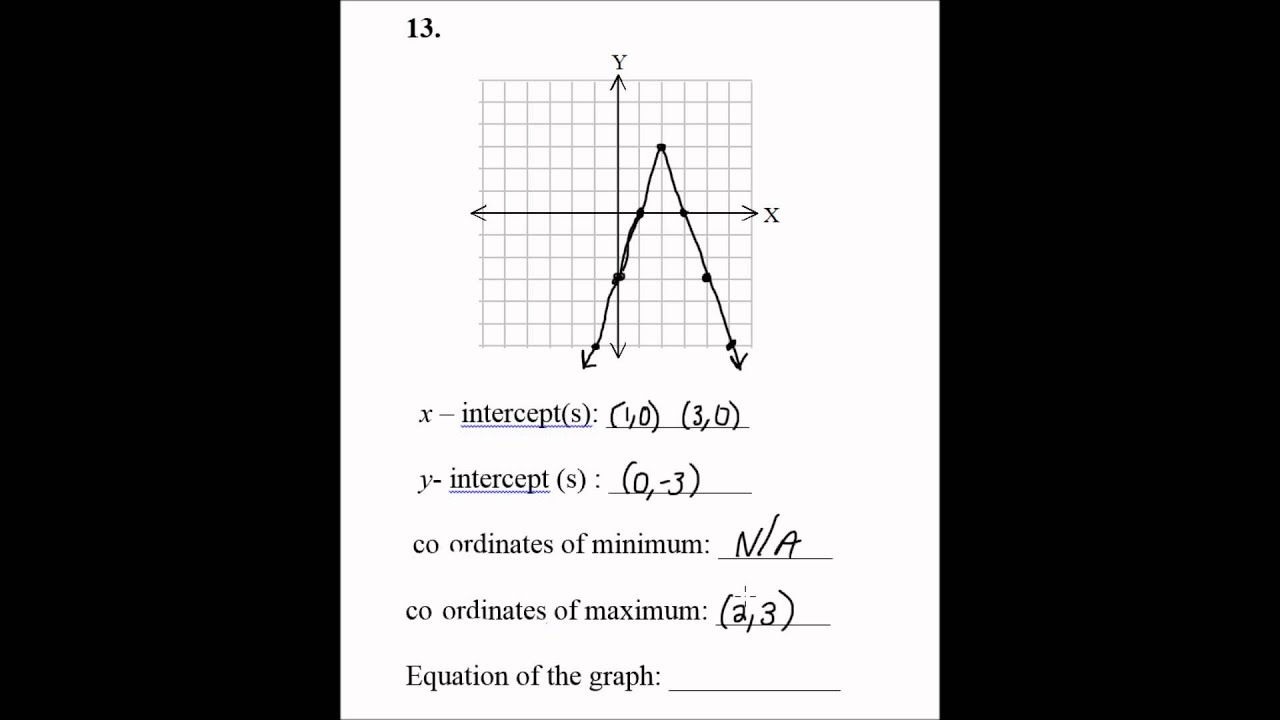
How To Write An Absolute Value Equation From A Graph – How To Write An Absolute Value Equation From A Graph
| Encouraged to the blog, on this period I will teach you concerning How To Clean Ruggable. And now, this is the first impression:
Why don’t you consider graphic above? is that incredible???. if you’re more dedicated thus, I’l d provide you with several image yet again below:
So, if you desire to receive all of these outstanding shots regarding (How To Write An Absolute Value Equation From A Graph), simply click save link to download these pictures to your personal pc. They’re ready for obtain, if you love and wish to have it, click save symbol in the page, and it’ll be immediately downloaded in your laptop computer.} As a final point if you need to get new and recent picture related with (How To Write An Absolute Value Equation From A Graph), please follow us on google plus or save this blog, we try our best to give you daily up-date with fresh and new graphics. We do hope you love staying here. For some up-dates and recent news about (How To Write An Absolute Value Equation From A Graph) shots, please kindly follow us on twitter, path, Instagram and google plus, or you mark this page on book mark area, We try to offer you up grade periodically with all new and fresh graphics, like your searching, and find the perfect for you.
Thanks for visiting our site, contentabove (How To Write An Absolute Value Equation From A Graph) published . At this time we’re delighted to declare we have discovered an awfullyinteresting contentto be discussed, namely (How To Write An Absolute Value Equation From A Graph) Most people attempting to find info about(How To Write An Absolute Value Equation From A Graph) and of course one of them is you, is not it?