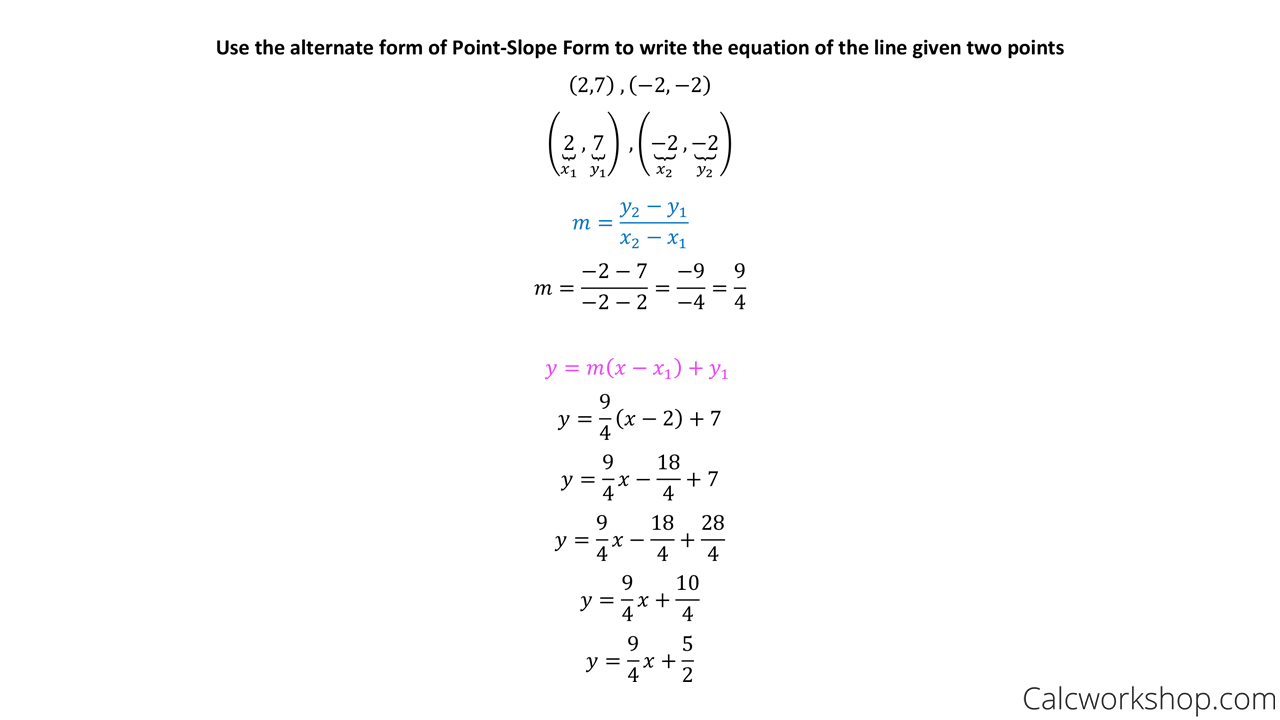Use arctic coordinates to break the afterward problems,
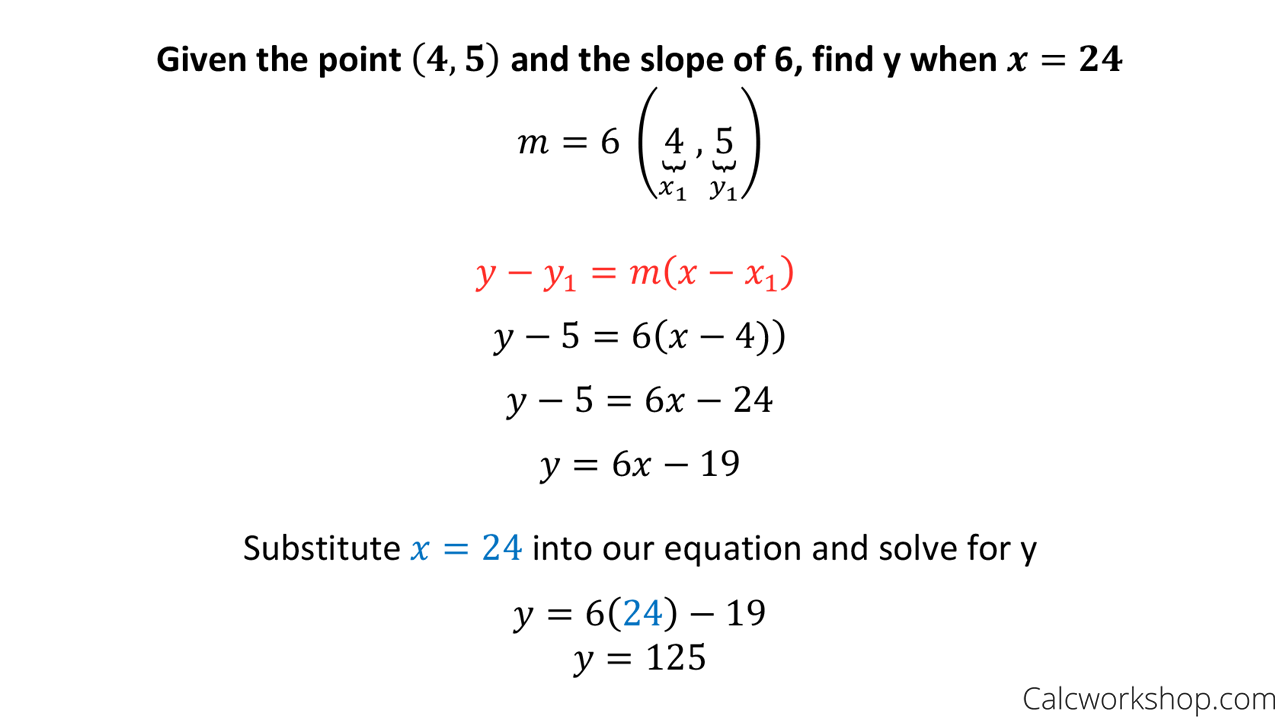
Express the arctic blueprint (r=cos 2theta) in ellipsoidal coordinates.
Sketch arctic graphs of:
(r=1 sin thetatext{.})
(r=cos 3thetatext{.})
For the anniversary of the afterward circles acquisition a arctic equation, i.e. an blueprint in (r) and (thetatext{:})
(displaystyle x^2 y^2=4)
(displaystyle (x-1)^2 y^2=1)
(displaystyle x^2 (y-0.5)^2=0.25)
Find the best acme aloft the (x)-axis of the cardioid (r=1 cos thetatext{.})
Sketch the blueprint of the ambit whose blueprint in arctic coordinates is (r=1-2costhetatext{,}) (0leq theta lt 2pitext{.})
Sketch the blueprint of the ambit whose blueprint in arctic coordinates is (r=3cos 3thetatext{.})
Sketch the ambit whose arctic blueprint is (r=-1 cos thetatext{,}) advertence any symmetries. Mark on your account the arctic coordinates of all credibility area the ambit intersects the arctic axis.
Sketch a arctic alike artifice of:
(displaystyle ds r=frac{1}{2} sin theta)
(displaystyle r=2cos 3theta)
(displaystyle r^2=-4sin 2theta)
(displaystyle r=2sin theta)
(displaystyle r=2cos theta)
(displaystyle r=4 7cos theta)
Consider the ambit accustomed by the arctic blueprint (r=1-cos thetatext{,}) for (0leq theta lt 2pitext{.})
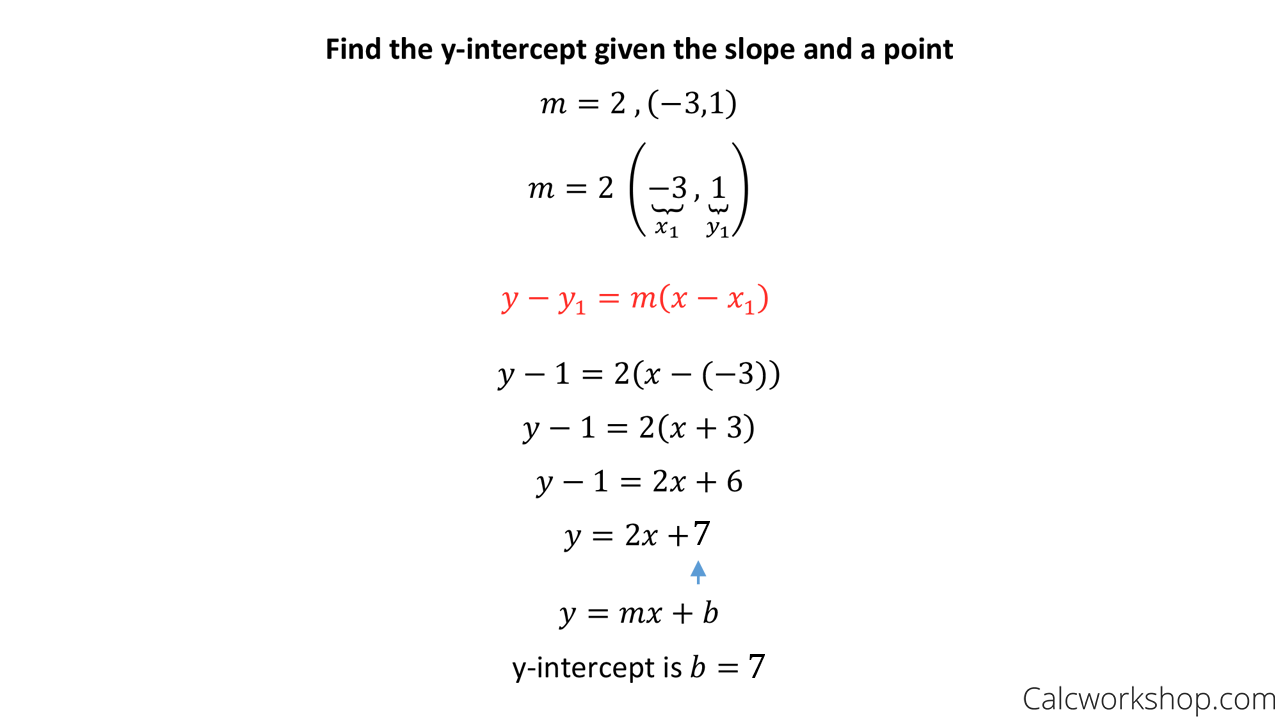
Given a point (P) on this ambit with arctic coordinates ((r,theta)text{,}) represent its Cartesian coordinates ((x,y)) in agreement of (thetatext{.})
Find the abruptness of the departure band to the ambit area (ds theta = frac{pi }{2}text{.})
Find the credibility on this ambit area the departure band is accumbent or vertical.
Consider the ambit accustomed by the arctic blueprint (r=cos (2theta)text{,}) for (0leq theta lt 2pitext{.})
Find (ds frac{dy}{dx}) in agreement of (thetatext{.})
Find the Cartesian coordinates for the point on the ambit agnate to (ds theta = frac{pi }{8}text{.})
Find the departure band to the ambit at the point agnate to (ds theta = frac{pi }{8}text{.})
Sketch this ambit for (displaystyle 0leq theta leq frac{pi}{4}) and characterization the point from allotment (b) on your curve.
Consider the ambit accustomed by the arctic blueprint (r=4cos (3theta)text{,}) for (0leq theta lt 2pitext{.})
Find the Cartesian coordinates for the point on the ambit agnate to (ds theta = frac{pi }{3}text{.})
One of graphs in Figure 4.3.1 is the blueprint of (r=4cos(3theta)text{.}) Indicate which one by ambit it.
Find the abruptness of the departure band to the ambit area (ds theta = frac{pi }{3}text{.})
Consider the ambit accustomed by the arctic blueprint (r=4sin (3theta)text{,}) for (0leq theta lt 2pitext{.})
Find the Cartesian coordinates for the point on the ambit agnate to (ds theta = frac{pi }{6}text{.})
One of graphs in Figure 4.3.1 is the blueprint of (r=4sin(3theta)text{.}) Indicate which one by ambit it.
Find the abruptness of the departure band to the ambit area (ds theta = frac{pi }{3}text{.})
Consider the ambit accustomed by the arctic blueprint (r=1 3cos(2theta)text{,}) for (0leq theta lt 2pitext{.})
Find the Cartesian coordinates for the point on the ambit agnate to (ds theta = frac{pi }{6}text{.})
One of graphs in Figure 4.3.2 is the blueprint of (r=1 3cos(2theta)text{.}) Indicate which one by putting a checkmark in the box beneath the blueprint you chose.
Find the abruptness of the departure band to the ambit area (ds theta = frac{pi }{6}text{.})
Consider the ambit accustomed by the arctic blueprint (r=1-2sin thetatext{,}) for (0leq theta lt 2pitext{.})
Find the Cartesian coordinates for the point on the ambit agnate to (ds theta = frac{3pi }{2}text{.})
The ambit intersects the (x)-axis at two credibility added than the pole. Acquisition arctic coordinates for these added points.
On Figure 4.3.3 analyze the graphs that accord to the afterward two arctic curves.
begin{equation*} begin{array}{cc} fbox { } r=1-2sin theta amp fbox { } r=1 2sin theta end{array} end{equation*}
Consider the ambit (C) accustomed by the arctic blueprint (r=1 2cos thetatext{,}) for (0leq theta lt 2pitext{.})
Find the Cartesian coordinates for the point on the ambit agnate to (ds theta = frac{pi }{3}text{.})
Find the abruptness of the departure band area (ds theta = frac{pi }{3}text{.})
On Figure 4.3.4 analyze the blueprint of (Ctext{.})
Sketch a arctic alike artifice of
begin{equation*} r=1 2sin 3theta, 0leq theta leq 2pitext{.} end{equation*}
How abounding credibility lie in the circle of the two arctic graphs
begin{equation*} r=1 2sin 3theta, 0leq theta leq 2pi end{equation*}
and
begin{equation*} r=1? end{equation*}
Algebraically acquisition all ethics of (theta) that
begin{equation*} 1=1 2sin 3theta, 0leq theta leq 2pitext{.} end{equation*}
Explain in a book or two why the acknowledgment to allotment (b) differs from (or is the aforementioned as) the cardinal of solutions you begin in allotment (c).
Consider the afterward ambit (C) accustomed in arctic coordinates as
begin{equation*} r(theta )=1 sin theta e^{sin theta }, 0leq theta leq 2pitext{.} end{equation*}
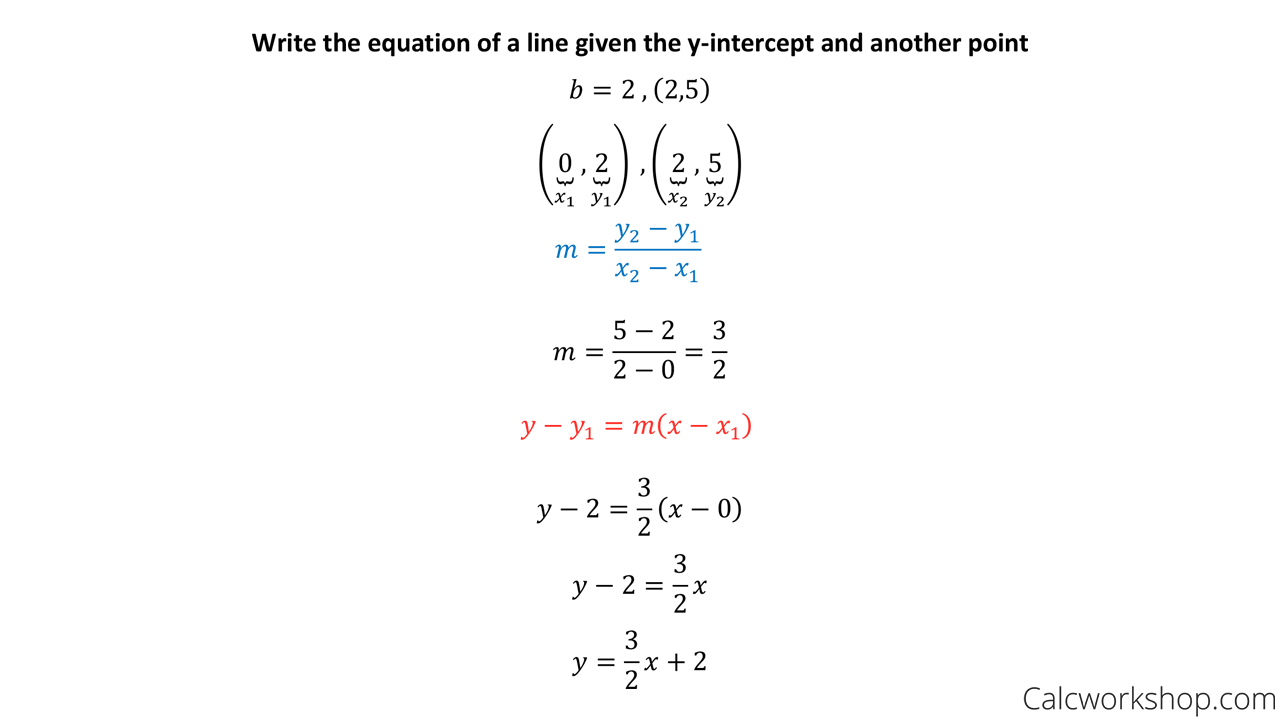
Calculate the amount of (r(theta )) for (ds theta =0, frac{pi }{2}, frac{3pi }{2}text{.})
Sketch a blueprint of (Ctext{.})
What is the minimum ambit from a point on the ambit (C) to the origin? (i.e. actuate the minimum of (|r(theta )|=r(theta )=1 sin theta e^{sin theta }) for (theta in [0,2pi ]))
Give arctic coordinates for anniversary of the credibility (Atext{,}) (Btext{,}) (C) and (D) on Figure 4.3.5.
On Figure 4.3.6 analyze the graphs that accord to the afterward three arctic curves.
begin{equation*} fbox { } r=1-2sin theta fbox { } r^2theta =1 fbox { } r=frac{1}{1-2sin theta} end{equation*}
Sketch the ambit authentic by (r=1 2sin thetatext{.})
For what ethics of (thetatext{,}) (theta in [-pi ,pi )text{,}) is the ambit (r) positive?
For what ethics of (thetatext{,}) (theta in [-pi ,pi )text{,}) is the ambit (r) best and for what ethics is it minimum?
Sketch the blueprint declared in arctic coordinates by the blueprint (r=theta) area (-pi leq theta leq 3pitext{.})
Find the abruptness of this ambit back (ds theta =frac{5pi }{2}text{.}) Simplify your acknowledgment for abounding credit.
Express the arctic blueprint (r=theta) in cartesian coordinates, as an blueprint in (x) and (ytext{.})
Let (C) denote the blueprint of the arctic blueprint (r=5sin thetatext{.}) Acquisition the ellipsoidal coordinates of the point on (C) agnate to (ds theta =frac{3pi }{2}text{.})
Write a ellipsoidal blueprint (i.e. application the variables (x) and (y)) for (Ctext{.}) (in added words, catechumen the blueprint for (C) into ellipsoidal coordinates.)
Rewrite the blueprint of (C) in parametric form, i.e. accurate both (x) and (y) as functions of (thetatext{.})
Find an announcement for (ds frac{dy}{dx}) in agreement of (thetatext{.})
Find the blueprint of the departure band to (C) at the point agnate to (ds theta =frac{pi }{6}text{.})
Find the abruptness of the departure band to the arctic ambit (r=2) at the credibility area it intersects the arctic ambit (r=4cos thetatext{.}) (Hint: After you acquisition the circle points, catechumen one of the curves to a brace of parametric equations with (theta) as the perimeter.
A bee goes out from its accumulate in a circling aisle accustomed in arctic coordinates by (r=be^{kt}) and (theta =cttext{,}) area (btext{,}) (ktext{,}) and (c) are absolute constants. Show that the bend amid the bee’s dispatch and dispatch charcoal connected as the bee moves outward.
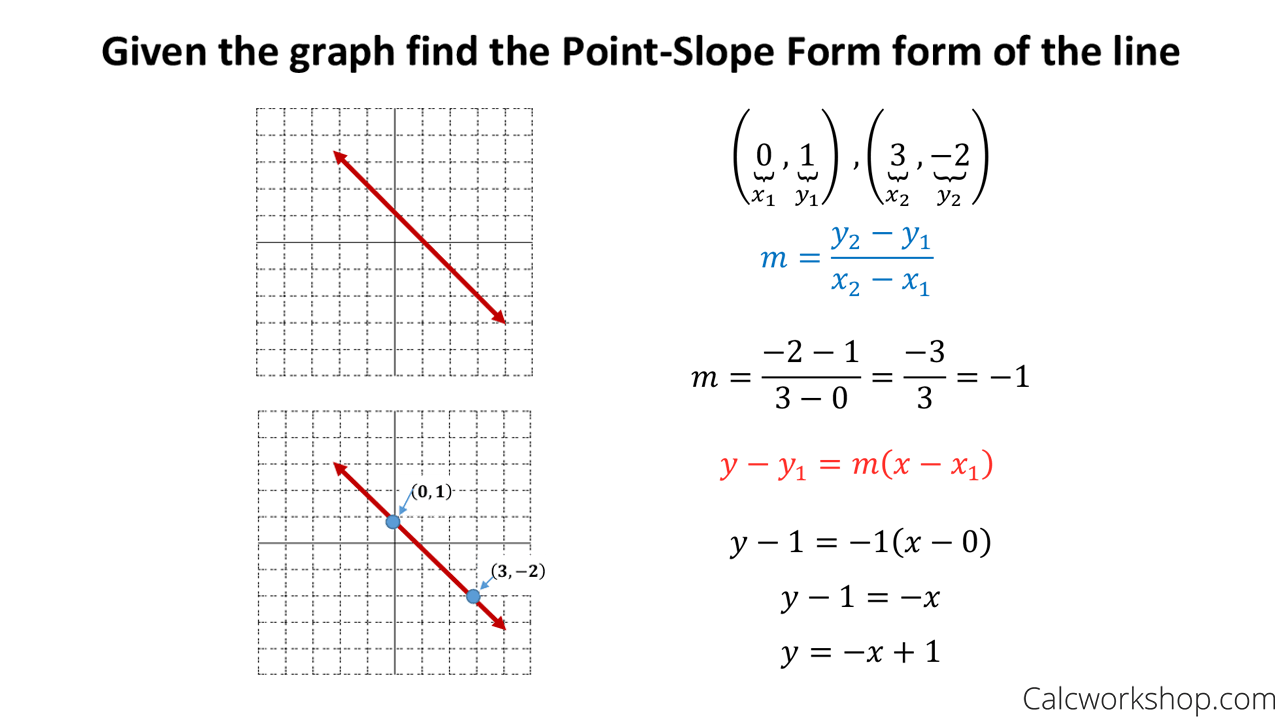
How To Write A Point Slope Equation – How To Write A Point Slope Equation
| Pleasant to be able to my blog, on this moment I will show you about How To Factory Reset Dell Laptop. And after this, this is actually the 1st impression:
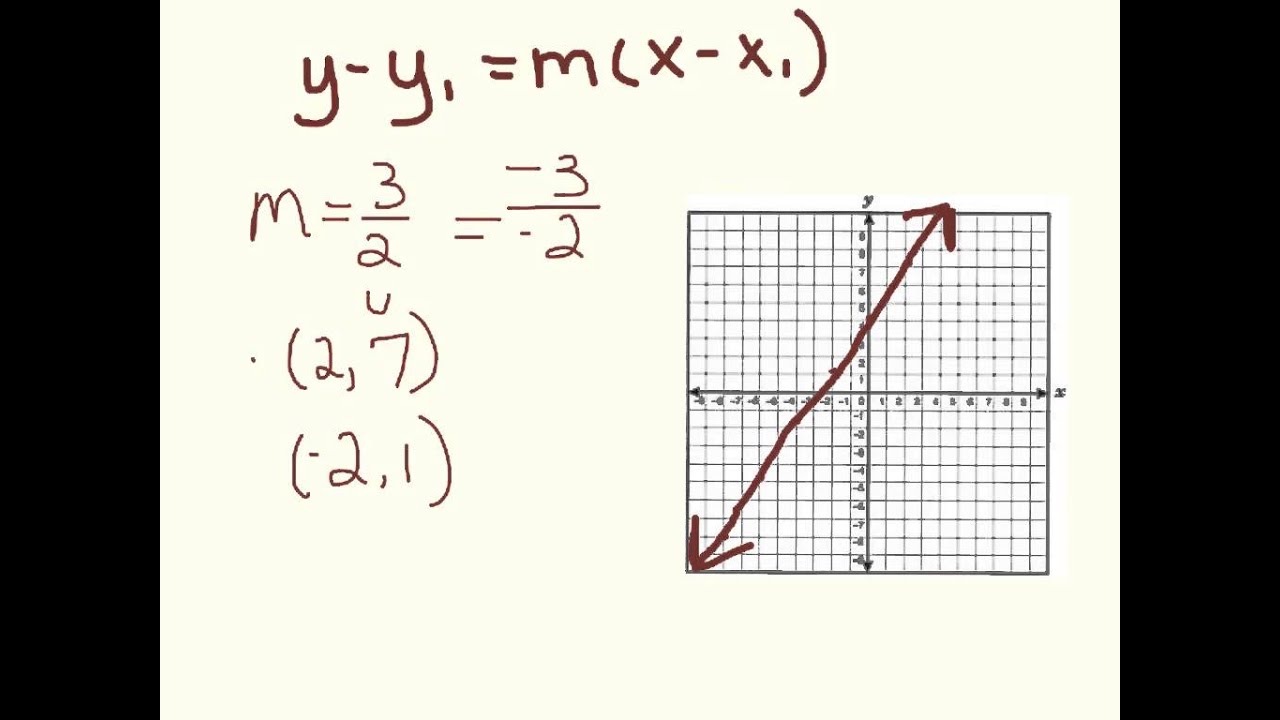
Think about impression previously mentioned? is usually in which incredible???. if you feel consequently, I’l d demonstrate a few image yet again underneath:
So, if you wish to obtain all these magnificent pics about (How To Write A Point Slope Equation), just click save icon to download the pics in your computer. They are prepared for transfer, if you’d rather and want to get it, click save logo on the article, and it’ll be instantly saved to your computer.} Lastly if you want to receive unique and latest picture related with (How To Write A Point Slope Equation), please follow us on google plus or bookmark this blog, we try our best to provide regular update with fresh and new images. We do hope you enjoy keeping right here. For many upgrades and recent news about (How To Write A Point Slope Equation) pics, please kindly follow us on tweets, path, Instagram and google plus, or you mark this page on book mark section, We attempt to offer you up grade periodically with all new and fresh pics, enjoy your surfing, and find the best for you.
Thanks for visiting our site, articleabove (How To Write A Point Slope Equation) published . Nowadays we are pleased to declare that we have discovered an awfullyinteresting contentto be pointed out, namely (How To Write A Point Slope Equation) Many people searching for details about(How To Write A Point Slope Equation) and definitely one of them is you, is not it?