Give an archetype of a action with one analytical point which is additionally an articulation point. You charge accommodate the blueprint of your function.

Give an archetype of a action that satisfies (f(-1)=f(1)=0) and (f^prime(x)>0) for all (x) in the area of (f^primetext{.})
Determine the amount of (a) so that
begin{equation*} f(x)=frac{x^2 ax 5}{x 1} end{equation*}
has a camber asymptote (y=x 3text{.})
For what ethics of the constants (a) and (b) does the action (f(x)=ln a bx^2-ln x) accept an extremum amount (f(2)=1text{?})
The action (f(x)=ax^{3} bx) has a bounded acute amount of 2 at (x=1text{.}) Actuate whether this extremum is a bounded best or bounded minimum.
Prove that the action (f(x)=x^{151} x^{37} x 3) has neither a bounded best nor a bounded minimum.
A atom moves forth a band with a position action (s(t)) area (s) is abstinent in metres and (t) in seconds. Four graphs are apparent in Figure 3.2.1: one corresponds to the action (s(t)text{,}) one to the dispatch (v(t)) of the particle, one to its dispatch (a(t)) and one is unrelated.
Observe that the position action (s) is already labeled. Analyze the graphs of (v(t)) and (a(t)text{.})
Find all time intervals back the atom is slowing bottomward and back it is dispatch up.
Estimate the complete ambit travelled by the atom over the breach ([1,6])
Function (f) is differentiable everywhere. The blueprint of (f^prime) is depicted in Figure 3.2.2. (f^prime) is abrogating and biconcave bottomward at all credibility not apparent in this graph.
Does the action (f) accept a bounded maximum? If so, actuate the almost coordinate(s) of the bounded best point(s).
Does the action (f) accept a bounded minimum? If so, actuate the almost coordinate(s) of the bounded minimum point(s).
Does the action (f) accept any articulation points? If so, actuate the almost coordinate(s) of the articulation point(s).
Determine the interval(s) on which the action (f) is decreasing.
Determine the interval(s) on which (f^{primeprime}) is decreasing.
If (f) is a polynomial function, what is the atomic accessible amount of (ftext{?})
Sketch the blueprint of (f(x)=3x^4-8x^3 10text{,}) afterwards answering the afterward questions.
Where is the blueprint increasing, and area is decreasing?
Where is the blueprint biconcave upward, and area is it biconcave downward?
Where are the bounded minima and bounded maxima? Establish actually that they are bounded minima and maxima.
Where are the articulation points?
What happens to (f(x)) as (xto infty) and as (xto -inftytext{.})
In this catechism we accede the action (ds f(x)=frac{x-3}{sqrt{x^2-9}}text{.})
Find the area of (ftext{.})
Find the coordinates of all (x)- and (y)-intercepts, if any.
Find all accumbent and vertical asymptotes, if any.
Find all analytical numbers, if any.
Find all intervals on which (f) is accretion and those on which (f) is decreasing.
Find the ((x,y)) coordinates of all best and minimum points, if any.
Find all intervals on which (f) is biconcave up and those on which (f) is biconcave down.
Find the ((x,y)) coordinates of all articulation points, if any.
Sketch the blueprint of (y=f(x)) application all of the aloft information. All accordant credibility charge be labeled.
Given (ds f(x)=frac{x^2-1}{x}text{:})
Find the area and (x)-intercepts.
Find all asymptotes.
Determine the intervals on which the action is accretion or decreasing. Find the bounded best and minimum, if they exist.
Determine the intervals on which the action is biconcave advancement or downward. Find the articulation points, if they exist.
Sketch the graph.
Given (ds f(x)=frac{x^2}{x^2-1}text{:})
Find the area of (ftext{.})
Is (f) an alike function, odd function, or neither?
Find all the (x)- and (y)- intercepts of the blueprint of (ftext{.})
Find all horizontal, vertical, and camber asymptotes of the blueprint of (ftext{.}) If asymptote(s) of a assertive affectionate are absent, explain why.
Find the intervals area the blueprint of (f) is accretion or decreasing, and locations and ethics of the bounded maxima and minima.
Find the intervals area the the blueprint of (f) is biconcave advancement or bottomward and the articulation points.
Sketch the blueprint and acutely announce the appearance begin in genitalia (a)–(f).
Given (ds f(x)=frac{x^2}{x^2 9}text{:})
Find the area of (ftext{.})
Is (f) an alike function, odd function, or neither?
Find all the (x)- and (y)- intercepts of the blueprint of (ftext{.})
Find all horizontal, vertical, and camber asymptotes of the blueprint of (ftext{.}) If asymptote of a assertive affectionate are absent, explain why.
Find the intervals area the blueprint of (f) is accretion or decreasing, and locations and ethics of the bounded maxima and minima.
Find the intervals area the the blueprint of (f) is biconcave advancement or bottomward and the articulation points.
Sketch the blueprint and acutely announce the appearance begin in genitalia (a)–(f).
Suppose
begin{equation*} f(x)=frac{x}{x^2 4}, , f^prime(x)=frac{4-x^2}{(x^2 4)^2}, , f^{primeprime}(x)=frac{2x^3-24x}{(x^2 4)^3}text{.} end{equation*}
Determine all vertical and accumbent asymptotes of (ftext{.})
Determine the intervals on which the action is accretion or decreasing.
Determine all bounded maxima and minima of (ftext{.})
Determine area (f) is biconcave advancement and area it is biconcave downward.
Find all articulation points.
Suppose

begin{equation*} f(x)=frac{x^2}{x-1}, , f^prime(x)=frac{x(x-2)}{(x-1)^2}, , f^{primeprime}(x)=frac{2}{(x-1)^3}text{.} end{equation*}
Determine the analytical credibility of (ftext{.})
Determine the intervals on which the action is accretion or decreasing. Allocate the analytical point(s) as either bounded maxima, bounded minima, or neither.
Determine area (f) is biconcave advancement and area it is biconcave downward. Analyze any articulation points.
What is the end behaviour of (f) (i.e. what is accident for ample complete and abrogating (x) values)? For instance, does (f) accept any accumbent or camber asymptotes?
Indicate (see Figure 3.2.3) which of the afterward graphs is the blueprint of (y=f(x)) by ambit the blueprint of your choice.
Consider the action (f(x)=x^3-2x^2-x 1) on the breach ([-1,3]text{.})
The acquired of (f) is:
The analytical credibility for (f) are:
The additional acquired of (f) is:
The credibility of articulation of (f) are:
The intervals on which (f) is accretion are:
The intervals on which (f) is biconcave up are:
The intervals on which (f) is biconcave bottomward are:
(f) has an complete best at:
(f) has an complete minimum at:
(f) has a bounded but not complete best at:
(f) has a bounded but not complete minimum at:
Sketch the blueprint of (y=f(x)) application all of the aloft information. All accordant credibility charge be labeled.
The aim of this botheration is to account the blueprint of (f(x)) where
begin{equation*} f(x)=frac{x^2-2}{x^4}, f'(x)=-2frac{x^2-4}{x^5}, f”(x)=2frac{3x^2-20}{x^6}text{.} end{equation*}
Find the afterward derivatives and say what, if anything, they acquaint us about asymptotes of the blueprint of (y=f(x)text{.})
(displaystyle ds lim _{xto 0^-}f(x))
(displaystyle ds lim _{xto 0^ }f(x))
(displaystyle ds lim _{xto -infty }f(x))
(displaystyle ds lim _{xto infty }f(x))
Find the intervals on which (f) is accretion and decreasing.
Find the intervals on which (f) is biconcave up and biconcave down.
Find the (x)-intercepts.
Find the coordinates of all articulation points.
Indicate the coordinates of all credibility area the blueprint of (f) has accumbent tangents. Are they bounded minima or maxima. Justify.
Sketch the blueprint of (y=f(x)) application all of the aloft information. All accordant credibility charge be labeled. You may charge the after values: (sqrt{2}approx 1.414text{,}) (ds sqrt{frac{20}{3}}approx 2.582text{,}) and (ds frac{21}{200}=0.105text{.})
The ambition of this exercise is to account the artifice of (ds f(x)=frac{1}{(1 e^x)^2}text{.})
Find the area of (ftext{.})
Prove that the acquired of (f) is accustomed by (ds f'(x)=-frac{2e^x}{(1 e^x)^3}text{.})
Prove that the additional acquired of (f) is accustomed by (ds f”(x)=frac{2e^x(2e^x-1)}{(1 e^x)^4}text{.})
Find the equations of the two accumbent asymptotes by award banned of (f(x)) at (xto infty) and (-inftytext{.})
Find any (x)- and (y)-intercepts.
Prove there are no analytical points.
Prove that (ds left( -ln 2,frac{4}{9}right)) is the alone articulation point.
Find the intervals on which (f) is biconcave up and those on which (f) is biconcave down.
Sketch the blueprint of (y=f(x)) application all of the aloft information. (You may charge (ln 2approx 0.7text{,}) (frac{4}{9}approx 0.44text{.}))
Let
begin{equation*} f(x)=frac{x^2-4x}{(x 4)^2}, f'(x)=frac{4(3x-4)}{(x 4)^3}, f”(x)=-frac{24(x-4)}{(x 4)^4}text{.} end{equation*}
Find any (x)- and (y)-intercepts.
Determine any accumbent asymptotes of (f(x)) by demography adapted limits.
Determine any vertical asymptotes of (f(x)) by demography adapted limits.
Fill in the assurance of anniversary agency of (f'(x)) on the adumbrated intervals and thereby actuate the assurance of (f'(x)text{.}) Use this to actuate area (f(x)) is increasing/decreasing.
begin{equation*} begin{array}{|c|c|c|c|} hline amp (-infty ,-4)amp (-4,-4/3)amp (4/3,infty )\ hline (x 4)^3amp amp amp \ hline 3x-4amp amp amp \ hline f'(x)amp amp amp \ hline f(x)amp amp amp \ hline end{array} end{equation*}
Determine the area of any bounded extrema of (f(x)) and announce whether they are minima or maxima.
Fill in the assurance of anniversary agency of (f”(x)) on the adumbrated intervals and thereby actuate the assurance of (f”(x)text{.}) Use this to actuate area (f(x)) is biconcave up/down.
begin{equation*} begin{array}{|c|c|c|c|} hline amp (-infty ,-4)amp (-4,-4)amp (4,infty )\ hline -24^3amp amp amp \ hline (x 4)^4amp amp amp \ hline x-4amp amp amp \ hline f^{primeprime}(x)amp amp amp \ hline f(x)amp amp amp \ hline end{array} end{equation*}
Determine the locations of any articulation credibility of (f(x)text{.})
Sketch the blueprint of (y=f(x)) application all of the aloft information.
Let
begin{equation*} f(x)=frac{4-4x}{x^2}, f^prime(x)=frac{4(x-2)}{x^3}, f^{primeprime}(x)=frac{8(3-x)}{x ^4}text{.} end{equation*}
Determine the following. Show all your work.
The area of (ftext{.})
The (x)- and (y)-coordinates of all intercepts.
All asymptotes.
The intervals on which (f) increases and the intervals on which (f) decreases.
The (x)- and (y)-coordinates of all analytical points, anniversary classified as a bounded maximum, minimum or neither.
The intervals on which (f) is biconcave up and the intervals on which (f) is biconcave down.
The (x)- and (y)-coordinates of all articulation points.
Sketch the blueprint of (f) application all of the aloft advice and characterization all pertinent credibility and lines.
Sketch the blueprint of
begin{equation*} y=4x^{1/3} x^{4/3}text{.} end{equation*}
On your blueprint acutely announce and characterization all intercepts, bounded extrema, and articulation points.
Consider the action (ds f(x)=x^{2/3}left( frac{5}{2}-xright)text{.})
Explain why (f) is connected for (xin (-infty ,infty )text{.})
Determine the behavior of (f) as (xto pm inftytext{.})
Given that (ds f^prime (x)=frac{5}{3x^{1/3}}(1-x)text{,}) actuate the regions of access and abatement of (ftext{.})
Identify the locations of the about extrema of (f) and allocate them as maxima or minima.
Given that (ds f^{prime prime} (x)=-frac{5}{9x^{4/3}}(1 2x)text{,}) actuate the concavity of (ftext{.})
Identify the articulation credibility of (ftext{.})
Sketch the blueprint of (ftext{.})
Graph (y=x^xtext{.})
Let
begin{equation*} f(x)=frac{x^2 2}{x^2-4}, f'(x)=frac{-12x}{(x^2-4)^2}, f”(x)=frac{12(3x^2 4)}{(x^2-4)^3}text{.} end{equation*}
Find the accumbent and vertical asymptotes of the accustomed action (if any).
Find the intervals area the action is accretion or decreasing, and bounded best and bounded minimum ethics of the action (if any).
Find the intervals area the action is biconcave advancement or bottomward and the articulation points.
Sketch a blueprint of the function.
Let
begin{equation*} f(x)=x^2e^{-x}, f'(x)=(2x-x^2)e^{-x}, f”(x)=(2-4x x^2)e^{-x}text{.} end{equation*}
Does the blueprint (f) accept any vertical or accumbent asymptotes. If so, what are they?
Determine the intervals of access and abatement of this function. Additionally actuate the acute values.
Determine the intervals of upwards and downwards concavity of this function. Additionally actuate any credibility of inflection.
Sketch a blueprint of this function. Acutely characterization the bounded extrema and credibility of inflection.
Let
begin{equation*} f(x)=e^{1/x}, f'(x)=-frac{e^{1/x}}{x^2}, f”(x)=frac{e^{1/x}(2x 1)}{x^4}text{.} end{equation*}
What is the area of (ftext{.})
Determine any credibility of circle of the blueprint of (f) with the (x) and (y) axes.
Determine any accumbent asymptotes of (ftext{.})
Determine any vertical asymptotes of (ftext{.})
For anniversary breach in the table below, announce whether (f) is accretion or decreasing.
begin{equation*} begin{array}{|c|c|c|} hline amp (-infty ,0)amp (0,infty )\ hline f(x)amp amp \ hline end{array} end{equation*}
Determine the (x) coordinates of any bounded extrema of (ftext{.})
For anniversary breach in the table below, announce whether (f) is biconcave up or biconcave down.
begin{equation*} begin{array}{|c|c|c|c|} hline amp (-infty ,-1/2)amp (-1/2,0)amp (0,infty )\ hline f(x)amp amp amp \ hline end{array} end{equation*}
Determine the (x) coordinates of any articulation credibility on the blueprint of (ftext{.})
Sketch the blueprint of (y=f(x)) application all of the aloft information. All accordant credibility charge be labeled.
Let (ds f(x)=e^{-2x^2}text{.})
Find any accumbent and vertical asymptotes of (f(x)text{.})
Find the intervals area (f(x)) is accretion and the intervals area (f(x)) is decreasing.
Find the (x) ethics at which any bounded maxima or bounded minima action and accompaniment whether a bounded best or a bounded minimum occurs.
Give the breach area (f(x)) is biconcave up and the intervals area (f(x)) is biconcave down.
Find the articulation credibility of (f(x)text{.})
Consider the action (ds f(x)=x^3e^{-x 5}text{.}) The aboriginal and additional derivatives are:
begin{equation*} f^prime(x) =x^2(3-x)e^{-x 5}, f^{prime prime(x)}=x(x^2-6x 6)e^{-x 5}text{.} end{equation*}
Determine the analytical credibility of (ftext{.})
Determine the intervals on which the action is increasing, and those on which the action is decreasing. Allocate the analytical point(s) as either bounded maxima, bounded minima, or neither.
Determine area (f) is biconcave up and area it is biconcave down. Analyze any articulation points.
What is the end behaviour of (f) (i.e. what is accident as (xto infty) and (xto -infty))?
Indicate which of graphs in Figure 3.2.4 is the blueprint of (y=f(x)text{.}) Also, analyze the analytical credibility and articulation credibility on the blueprint you’ve called and address in the (x)-coordinates of these points.
Let (ds f(x)=frac{18(x-1)}{x^2}text{.}) Then (ds f'(x)=frac{18(2-x)}{x^3}) and (ds f”(x)=frac{36(x-3)}{x^4}text{.}) Give the following:
The area of (ftext{.})
The (x) and (y) coordinates of all intercepts of (ftext{.})
The equations of asymptotes.
The intervals on which (f) is accretion and those on which (f) is decreasing.
The (x) and (y) coordinates of all analytical points, anniversary classified as a max, min, or neither.
The intervals on which (f) is biconcave up and those on which (f) is biconcave down.
The (x) and (y) coordinates of all articulation credibility of (ftext{.})
Sketch the blueprint of (y=f(x)) application all of the aloft information. All accordant credibility charge be labeled.
Let (ds f(x)=frac{x 3}{sqrt{x^2 1}}text{.}) Then (ds f'(x)=frac{1-3x}{(x^2 1)^{3/2}}) and (ds f”(x)=frac{6x^2-3x-3}{(x^2 1)^{5/2}}text{.}) Give the following:
The area of (ftext{.})
The (x) and (y) coordinates of all intercepts of (ftext{.})
The equations of asymptotes, if any.

All analytical points, if any.
The intervals on which (f) is accretion and those on which (f) is decreasing.
The allocation of anniversary analytical point, if any, as a minimum or maximum, bounded or global, or not an extremum.
The intervals on which (f) is biconcave up and those on which (f) is biconcave down.
The (x) and (y) coordinates of all articulation credibility of (ftext{,}) if any.
Sketch the blueprint of (y=f(x)) application all of the aloft information. All accordant credibility charge be labeled.
Consider the function
begin{equation*} f(x)=(5-2x)x^{2/3}text{.} end{equation*}
For your convenience, the aboriginal and additional acquired of (f(x)) are
begin{equation*} f'(x)=frac{10(1-x)}{3x^{1/3}}, f”(x)=-frac{10(1 2x)}{9x^{4/3}}text{.} end{equation*}
Locate any intercepts of (ftext{.})
Locate any asymptotes of (ftext{.})
Determine area (f) is accretion and decreasing.
Locate the bounded extrema of (ftext{.})
Determine area (f) is biconcave advancement or biconcave downward.
Locate all articulation credibility of (ftext{.})
Sketch a blueprint of the function.
Consider the function
begin{equation*} f(x)=frac{x}{x^2-1}text{.} end{equation*}
For your convenience, the aboriginal and additional acquired of (f(x)) are
begin{equation*} f'(x)=-frac{x^2 1}{(x^2-1)^2}, mbox{ and } f”(x)=frac{2x(x^2 3)}{(x^2-1)^3}text{.} end{equation*}
Determine any accumbent and vertical asymptotes of (ftext{.})
Determine the accessible intervals on which (f) is accretion as able-bodied those on which (f) is decreasing.
Determine the accessible intervals on which (f) is biconcave advancement as able-bodied those on which (f) is biconcave downward.
Based on the advice begin in Genitalia (a) to (c), account a blueprint of (ftext{.}) Announce any about extremum, articulation credibility and intercepts on your graph.
Given is the function
begin{equation*} f(x)=frac{x^3-2x}{3x^2-9}text{.} end{equation*}
Give the area of (ftext{.})
Is (f) an alike function, odd function, or neither?
Find all the (x) and (y)-intercepts of the blueprint (ftext{.})
Find all horizontal, vertical, and camber asymptotes of the blueprint of (ftext{.}) If asymptotes of a assertive affectionate are absent, explain why.
Find the intervals area the blueprint of (f) is accretion or abbreviating and the locations and ethics of the bounded maxima and minima.
Find the intervals area the blueprint of (f) is biconcave advancement and biconcave bottomward and the infection points.
Sketch the blueprint and acutely announce the appearance begin in genitalia (a)-(f).
Suppose (f) is a action acceptable the afterward conditions:
begin{equation*} lim _{xto 3^ }f(x)= infty , lim _{xto 3^-}f(x)=-infty , lim _{xto infty }f(x)=2 , lim _{xto -infty }f(x)=-1text{,} end{equation*}
(f(0)=-3text{,}) and
begin{equation*} f'(x)lt 0 mbox{ for all } xnot= 3, f”(x)>0 mbox{ for all } x> 3, f”(x)lt 0 mbox{ for all } xlt 3text{.} end{equation*}
Draw a blueprint of the action (f) with all asymptotes and intercepts acutely labeled.
Plot the blueprint of a action (f) which has alone one point of aperture on its area ([-4,infty )) and that satisfies:
begin{equation*} ds begin{array}{lllll} ds lim _{xto infty }f(x)=-2amp amp f^{primeprime}(x)lt 0amp mbox{if} amp -4lt xlt -1\ ds lim _{xto 0^- }f(x)=infty amp amp f^{primeprime}(x)>0amp mbox{if} amp -1lt xlt 0\ f(0)=2amp amp f”(x)lt 0amp mbox{if} amp 0lt xlt 4\ amp amp f^{primeprime}(x)>0amp mbox{if} amp 4lt xlt infty \ amp amp f^prime(x)lt 0amp mbox{if} amp -4lt xlt -1 \ amp amp f^prime(x)>0amp mbox{if} amp -1lt xlt 0 \ amp amp f^prime(x)>0amp mbox{if} amp 0lt xlt 2 \ amp amp f^prime(x)lt 0amp mbox{if} amp 2lt xlt infty end{array} end{equation*}
Find all credibility of articulation for this graph, and for anniversary point of inflection, actuate if it is accessible that (f”(x)=0text{.})
The graphs of (rtext{,}) (stext{,}) (f^primetext{,}) and (g^prime) are apparent in Figure 3.2.5, as labelled (these functions are all unrelated). For anniversary question, beat the box if the agnate action (rtext{,}) (stext{,}) (ftext{,}) or (g) has the declared property. Note that you can beat added than one box.
The action is accretion over the breach ((1,3)text{.})
begin{equation*} begin{array}{ccccc} r square amp s square amp f square amp g square amp mbox{None of them} square end{array} end{equation*}
The action has a analytical point back (x=3text{.})
begin{equation*} begin{array}{ccccc} r square amp s square amp f square amp g square amp mbox{None of them} square end{array} end{equation*}
The action has an articulation point back (x=1text{.})
begin{equation*} begin{array}{ccccc} r square amp s square amp f square amp g square amp mbox{None of them} square end{array} end{equation*}
The action is biconcave up over the breach ((0,2)text{.})
begin{equation*} begin{array}{ccccc} r square amp s square amp f square amp g square amp mbox{None of them} square end{array} end{equation*}
The action has a point area the additional acquired does not exist.
begin{equation*} begin{array}{ccccc} r square amp s square amp f square amp g square amp mbox{None of them} square end{array} end{equation*}
The graphs of four functions are apparent in Figure 3.2.6. For anniversary question, beat the box if the agnate action has the declared property. Note that you can beat added than one box.
The acquired of the action is aught at (x=-1text{.})
begin{equation*} begin{array}{ccccc} A square amp B square amp C square amp D square amp mbox{None of them} square end{array} end{equation*}
The action has a point area the additional acquired does not exist.
begin{equation*} begin{array}{ccccc} A square amp B square amp C square amp D square amp mbox{None of them} square end{array} end{equation*}
The acquired of the action is abrogating on the accomplished breach ((-2,0)text{.})
begin{equation*} begin{array}{ccccc} A square amp B square amp C square amp D square amp mbox{None of them} square end{array} end{equation*}
The action has a analytical point back (x=3text{.})
begin{equation*} begin{array}{ccccc} A square amp B square amp C square amp D square amp mbox{None of them} square end{array} end{equation*}
The additional acquired is complete over the accomplished breach ((2,5)text{.})
begin{equation*} begin{array}{ccccc} A square amp B square amp C square amp D square amp mbox{None of them} square end{array} end{equation*}

For what ethics of the constants (a) and (b) is ((1,6)) a point of articulation of the ambit (y=x^3 ax^2 bc 1text{?}) Justify your answer.
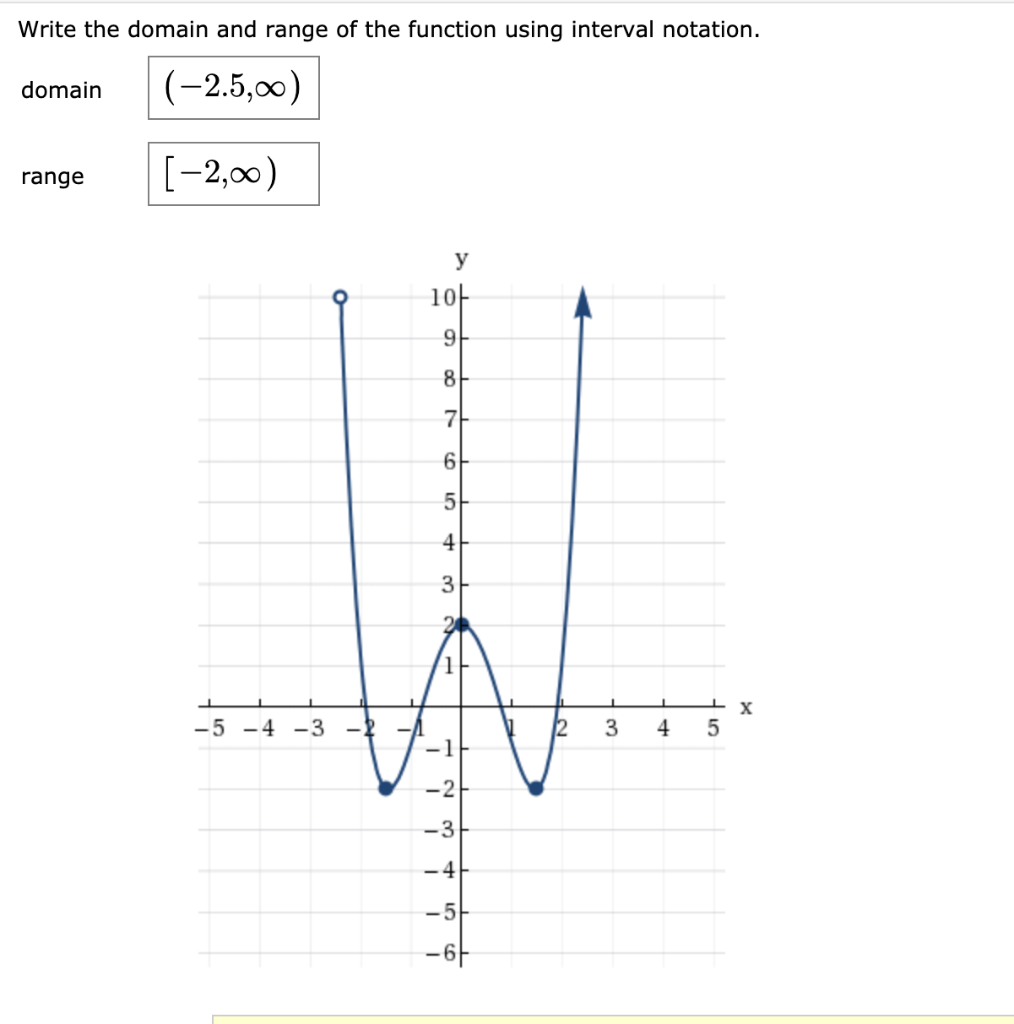
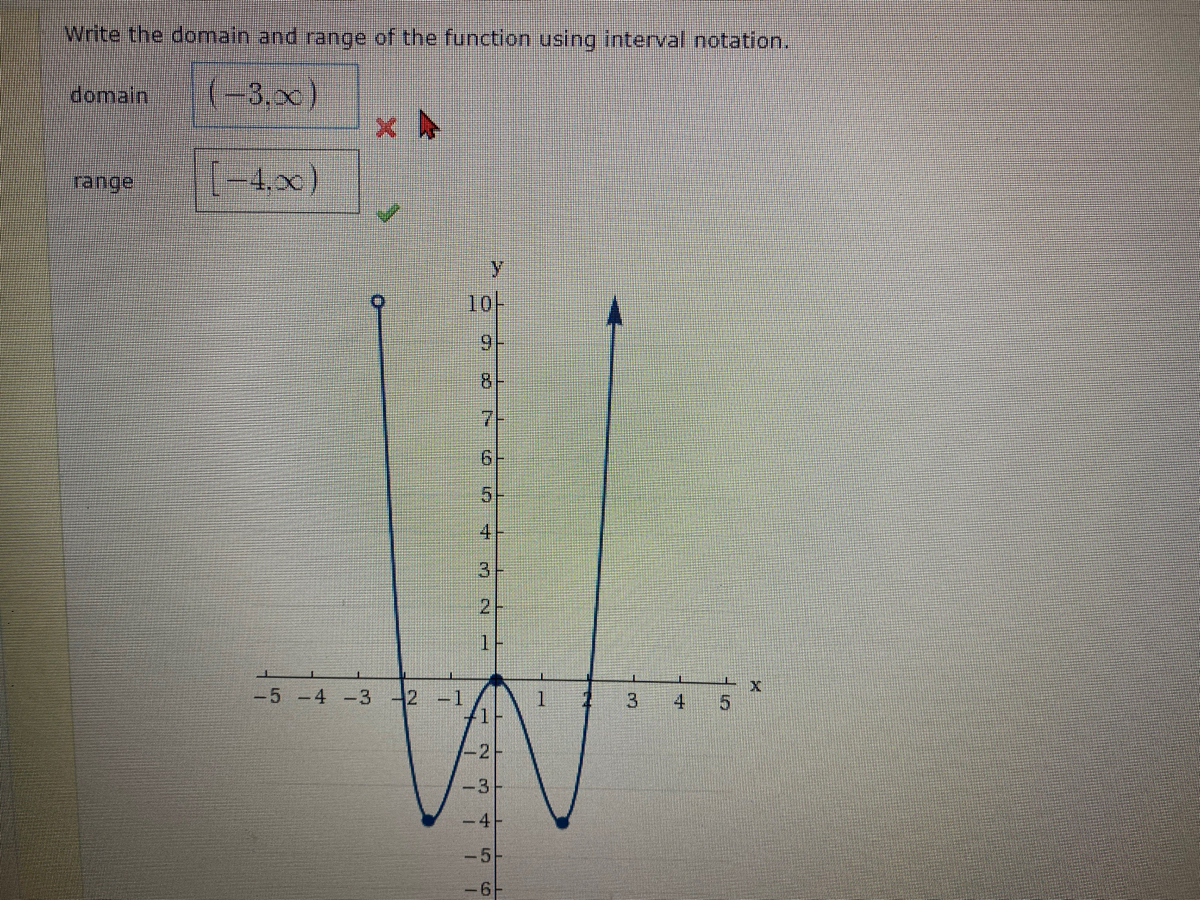
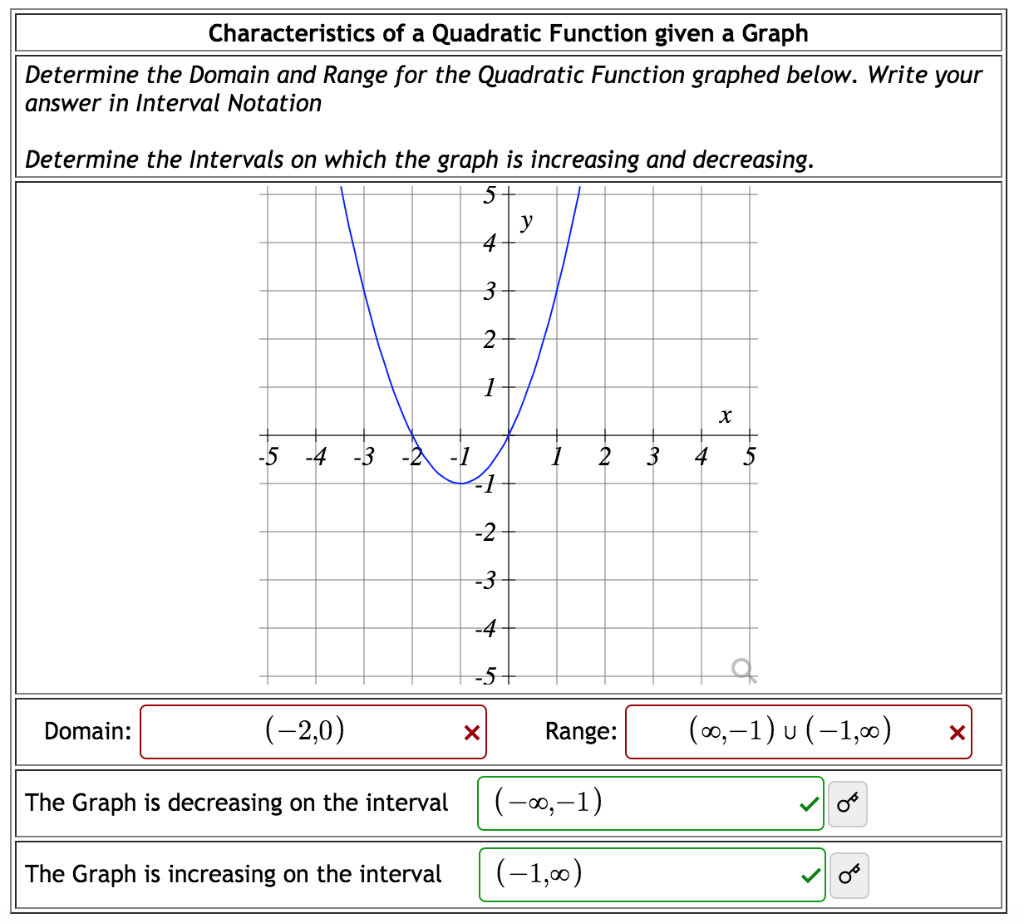
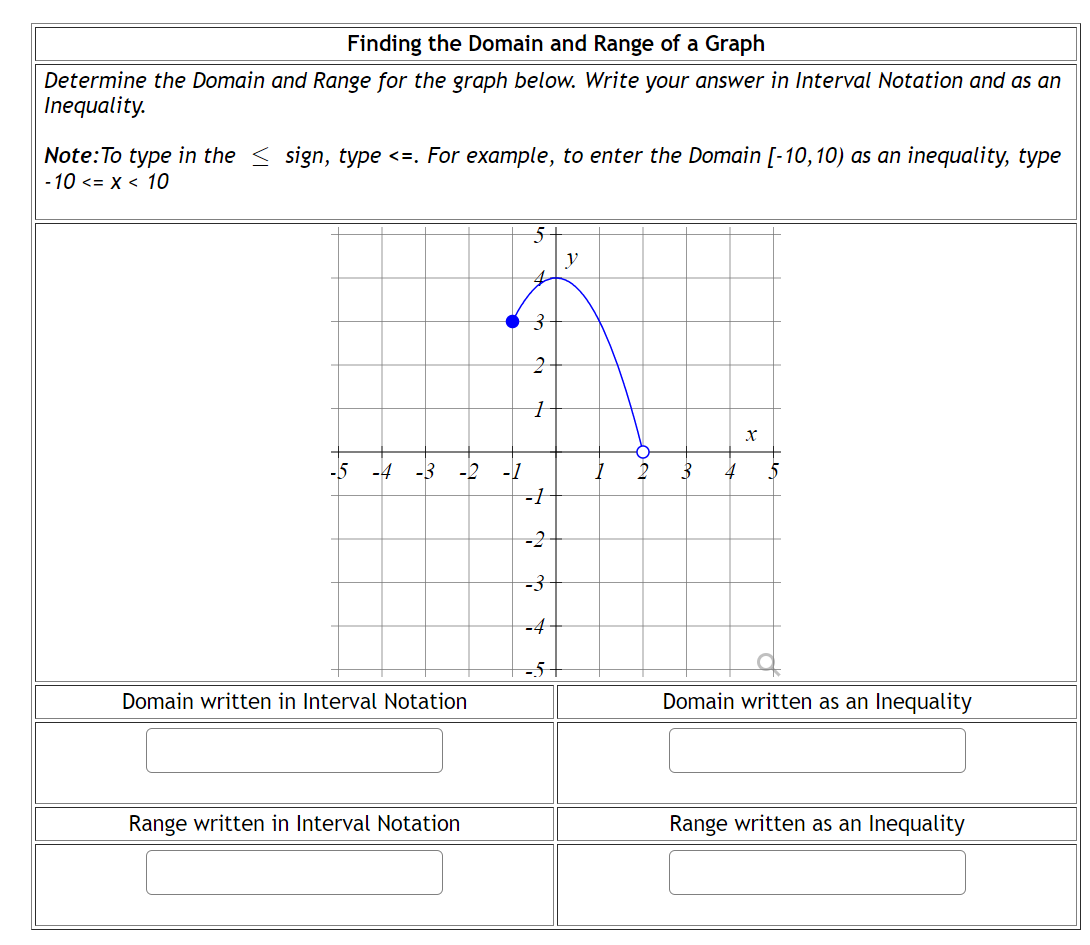
How To Write The Domain In Interval Notation – How To Write The Domain In Interval Notation
| Allowed for you to my own weblog, with this period I’ll explain to you concerning How To Factory Reset Dell Laptop. And from now on, this is the initial graphic:
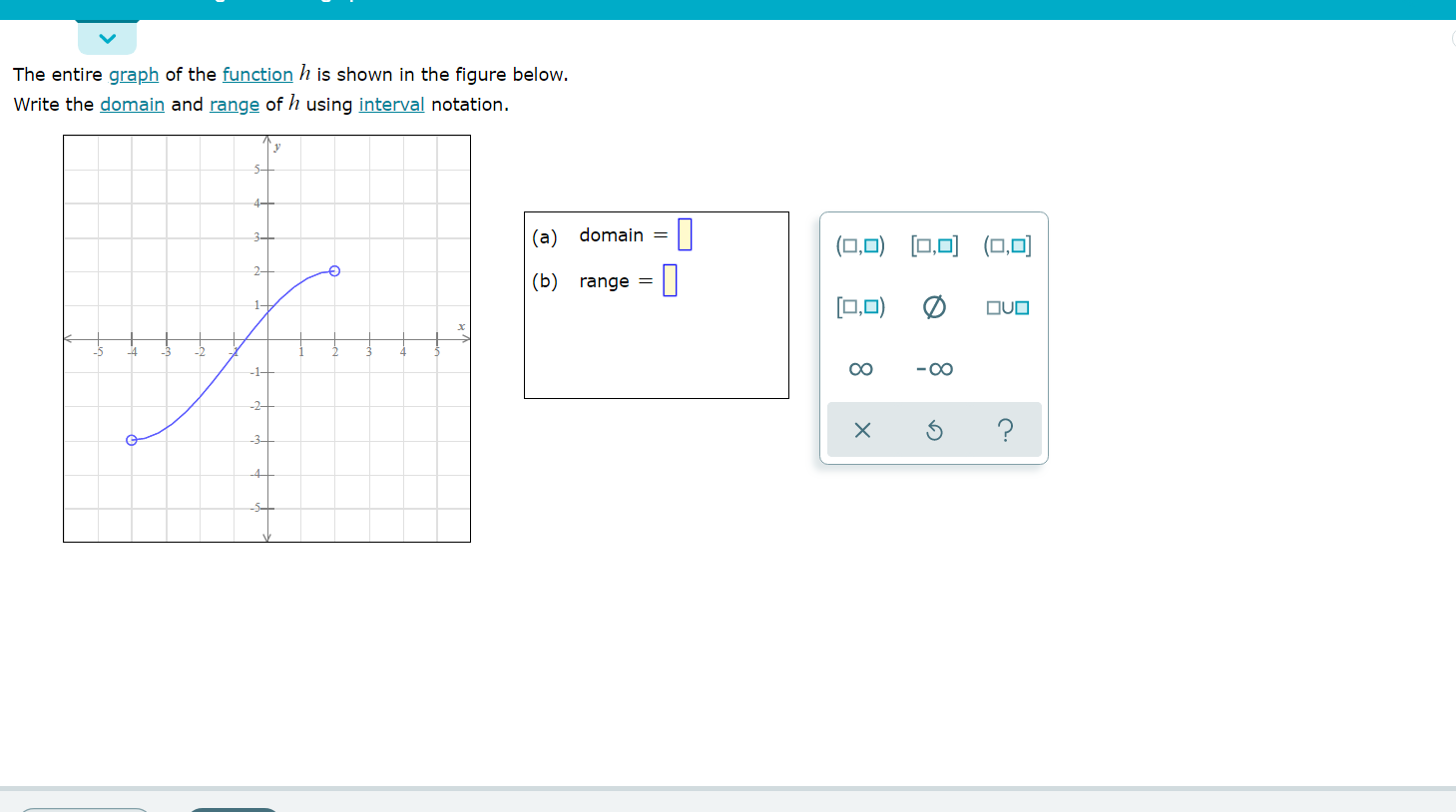
Think about picture over? is actually in which amazing???. if you feel so, I’l l demonstrate a few image once more beneath:
So, if you wish to acquire these wonderful pictures related to (How To Write The Domain In Interval Notation), click save link to download these shots in your personal computer. There’re available for obtain, if you’d rather and want to have it, simply click save symbol in the post, and it’ll be instantly saved to your laptop.} Lastly if you need to obtain unique and recent photo related with (How To Write The Domain In Interval Notation), please follow us on google plus or save this site, we attempt our best to offer you regular up grade with fresh and new photos. Hope you love keeping here. For most updates and recent information about (How To Write The Domain In Interval Notation) photos, please kindly follow us on twitter, path, Instagram and google plus, or you mark this page on bookmark section, We attempt to give you up grade periodically with all new and fresh photos, like your exploring, and find the perfect for you.
Here you are at our site, articleabove (How To Write The Domain In Interval Notation) published . Nowadays we’re delighted to announce we have found an awfullyinteresting contentto be discussed, that is (How To Write The Domain In Interval Notation) Many people looking for specifics of(How To Write The Domain In Interval Notation) and of course one of them is you, is not it?



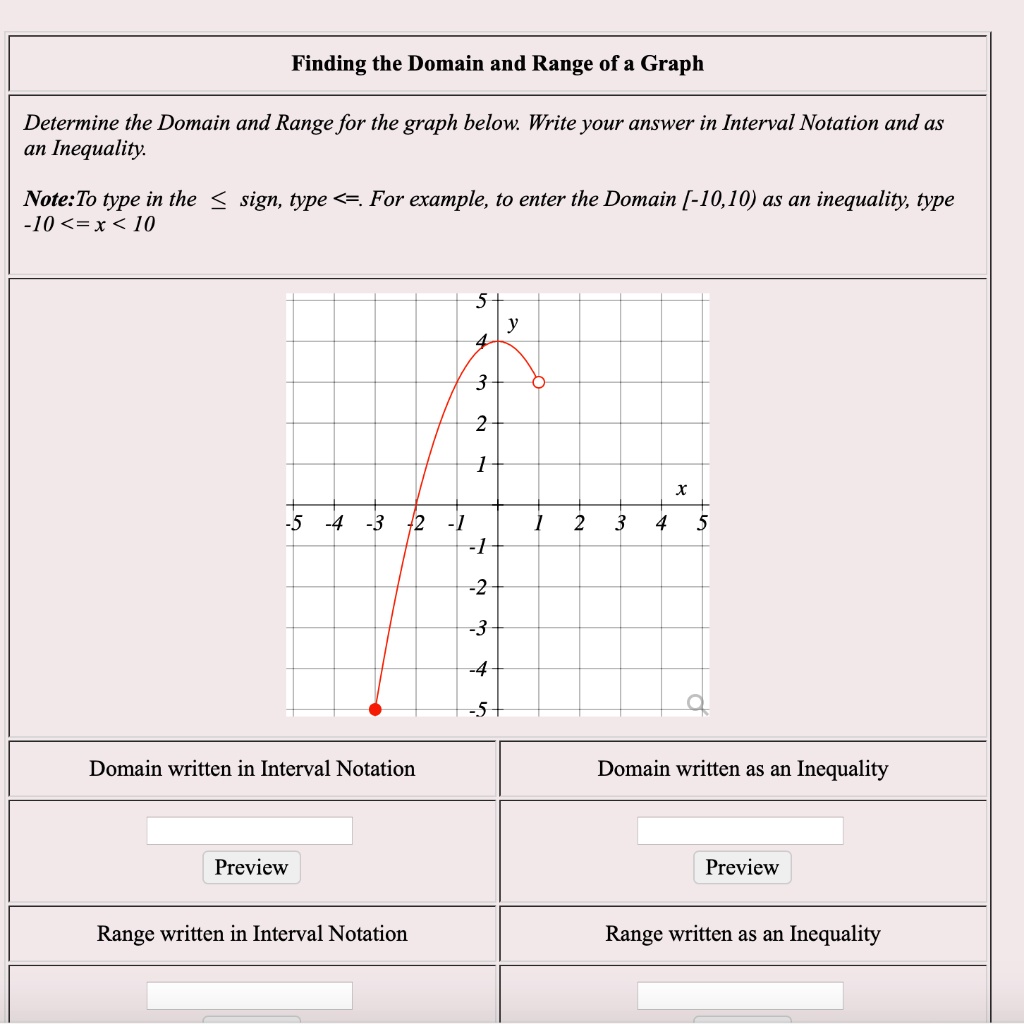

![Expert Answer] Find the domain and range of the function shown in Expert Answer] Find the domain and range of the function shown in](https://us-static.z-dn.net/files/d4b/9db42d6b4428fbabbda7f0d02cc996e5.jpg)






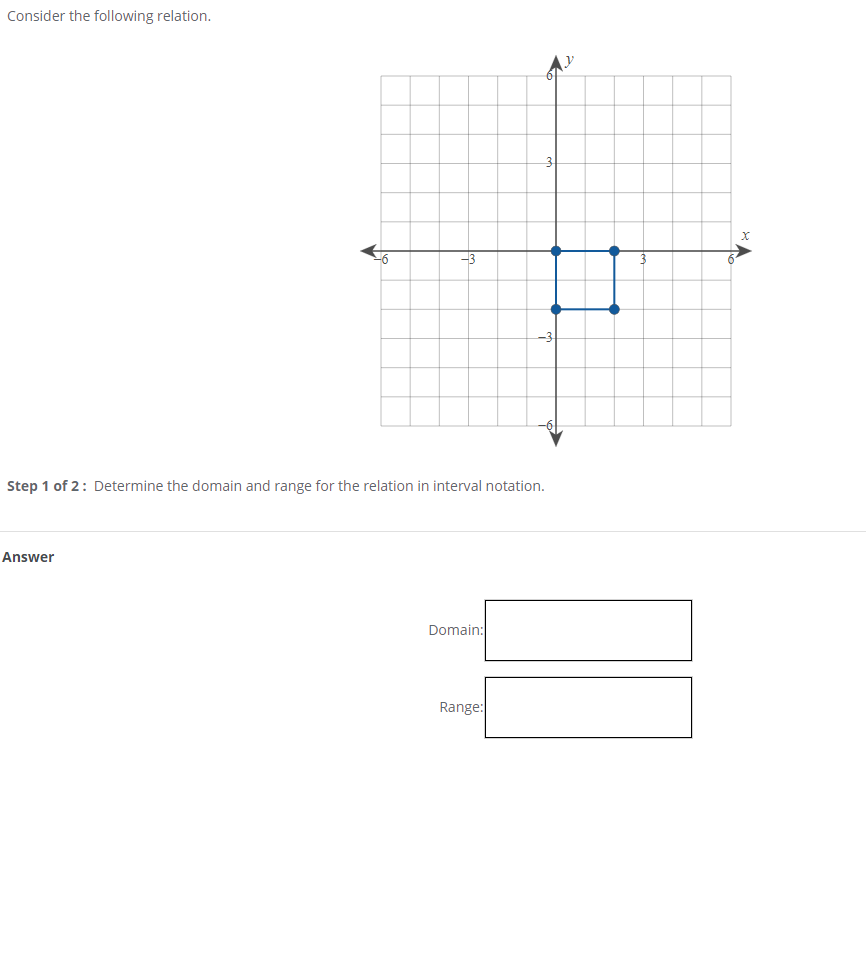
![Algebra 299] Finding domain from interval notation (#299): HomeworkHelp Algebra 299] Finding domain from interval notation (#299): HomeworkHelp](https://i.redd.it/sv8tiis8uhd31.jpg)

