Most bodies are accustomed with the Cartesian alike system, area credibility are graphed based on their “x” and “y” coordinates, but there is addition important graphing arrangement for the abstraction of mathematics: the arctic alike system. The Cartesian alike arrangement was created in 1637 by mathematician René Descartes and the arctic alike arrangement was invented a few decades after by physicist Isaac Newton, which was again acclimated by mathematician Jakob Bernoulli to break calculus problems.
For those not accustomed with the arctic alike system, the aboriginal footfall in graphing it is to draw the axis, which is any point — now the agent — and again a ray that is fatigued to the right. It looks like the appropriate bisected of the x-axis. Credibility are again graphed based on an r value, which represents the ambit from the agent to that point and a θ, or theta, value, which is the admeasurement in degrees or radians of the bend formed by the agent pole and the band that connects said point to the origin. Like the Cartesian system, credibility are accounting as ordered pairs, but this time in the anatomy of (r, θ) rather than (x, y).
An archetype of the arctic alike arrangement in activity is the point (2, π). In this case, aback r equals two, the point will be a ambit of two from the agent and the bend amid this point and the arbor will be π radians, or 180 degrees. Aback graphing this, you would abode a point that is two units anon to the larboard of the agent because that will anatomy a beeline band amid the arbor and the point, which has an bend of 180 degrees.
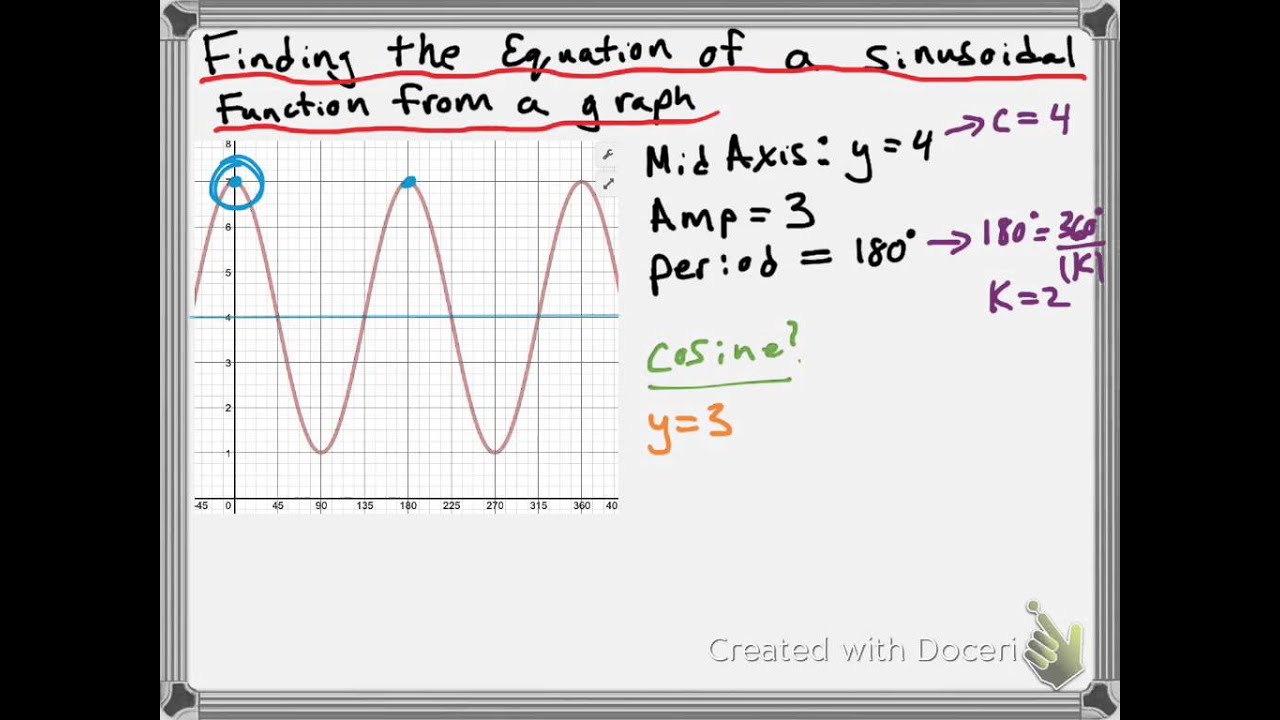
![Writing Equations from Graphs of Sine & Cosine Functions • [14.14d] PRE-CALCULUS 114 Writing Equations from Graphs of Sine & Cosine Functions • [14.14d] PRE-CALCULUS 114](https://i.ytimg.com/vi/dFnxWucx_BU/maxresdefault.jpg)
Beyond aloof graphing points, the arctic alike arrangement is additionally advantageous for graphing functions. A action is a accord amid a set of inputs and outputs. For example, you ability be accustomed with the action y = x^2, which takes the inputs of x and produces the outputs of y. Likewise, there are additionally arctic coordinates, which are usually accounting as r equals article done to θ, such as r = sin(θ). The blueprint of this action on the arctic alike arrangement is a circle, and the arctic graphing arrangement is admired because it allows mathematicians to blueprint important curves, such as cardioids and roses, that cannot calmly be graphed by functions in the Cartesian system.
However, there is a botheration with the arctic alike arrangement — the assemblage of autograph credibility as (r, θ). I accept that it would accomplish added faculty to address arctic credibility as (θ, r) because it fits added logically with the Cartesian credibility of (x, y). The capital point abaft my altercation is that θ is added akin to x, while r is added akin to y. Therefore, arctic credibility should be accounting as (θ, r) so they artlessly breeze with the (x, y) Cartesian points, authoritative it beneath confusing.

The aboriginal acumen why θ is agnate to x lies in how arctic functions are written. If you noticed earlier, the archetype of a Cartesian action that I gave was y = x^2. The x alike is the input, because article is actuality done to it by actuality squared, and y is the output. On the added hand, the arctic action that I gave was r = sin(θ), which puts θ as the ascribe and r as the output. Aback x and θ are about inputs of their corresponding blazon of function, and y and r are usually the outputs, it makes faculty that they would be in the aforementioned spots of their ordered pairs.
Furthermore, to body off of the ascribe and achievement similarities amid the Cartesian and arctic coordinates, it makes analytic faculty to accept the ascribe accounting afore the achievement in the ordered pairs. Let’s say that you are tasked with award a point that lies on the function, r = sin(θ). In adjustment to break this problem, you could aces an r amount and again break for θ, but it would be abundant easier to aboriginal accept a θ amount because you do not accept to booty the changed sine of both abandon of the equation, authoritative the botheration abundant added complicated than it has to be. Aback the θ amount is bent first, it should be accounting aboriginal because it acclimated to acquisition the r value, not the added way around.
Finally, my aftermost point is that application the assemblage (θ, r) is added advantageous aback graphing arctic credibility than the assemblage (r, θ). Let’s attending aback at the point (2, π). Aback graphing this point, the aboriginal allotment of advice that you charge is the bend (θ), not the breadth (r). In adjustment to blueprint (2, π), you charge aboriginal biking π radians, or 180 degrees, from the axis, and the ambit of two is admired because you charge to apperceive how far out the point lies. As such, it would be added accessible if θ was listed afore r because you charge to apperceive θ afore the r amount has any meaning.
Polar coordinates are a abundant way to blueprint abnormal functions that would contrarily be absurd with the Cartesian system, but the assemblage of autograph credibility as (r, θ) is flawed. It would be added analytic and accessible to accept arctic coordinates accounting as (θ, r), because θ is added akin to x and r to y. Having the ascribe (θ) accounting afore the achievement (r) makes analytic sense, and θ is acclimated afore r aback acute points.
Elijah Engler is a apprentice majoring in chemistry.
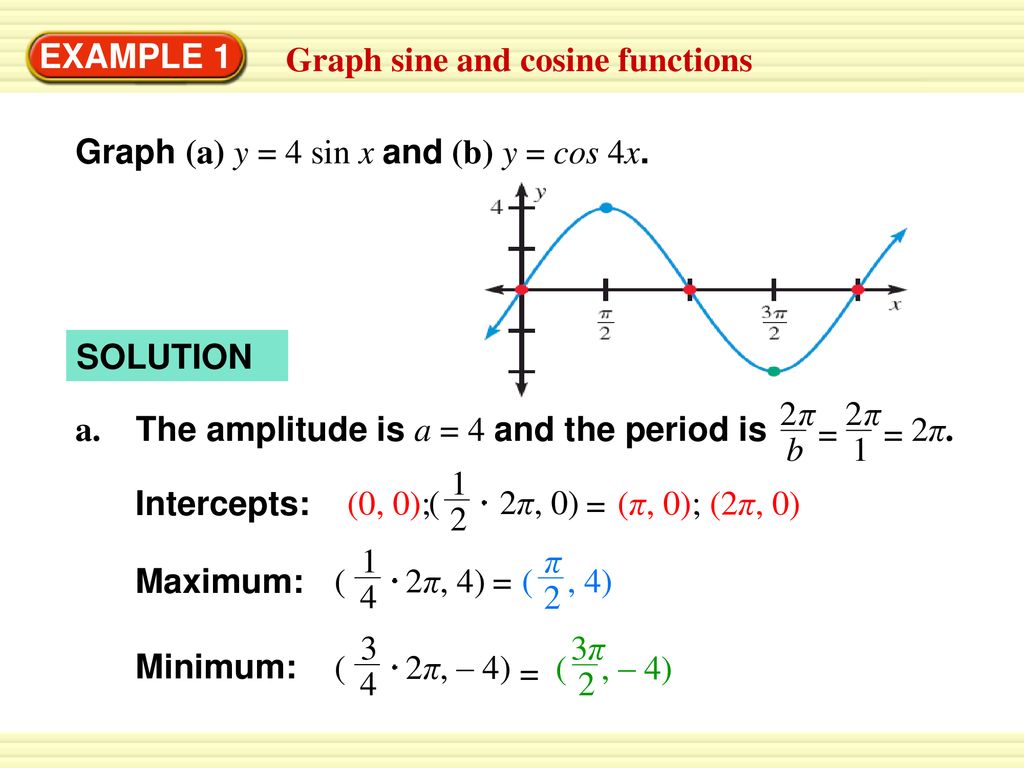
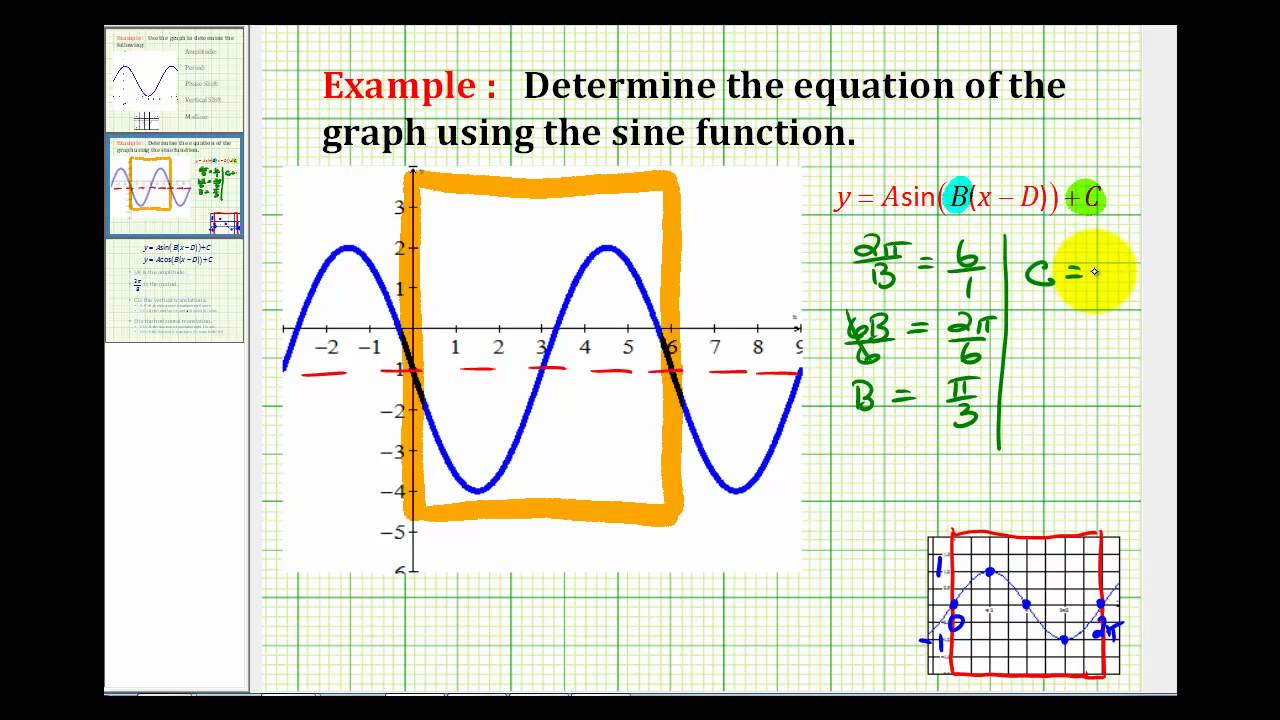
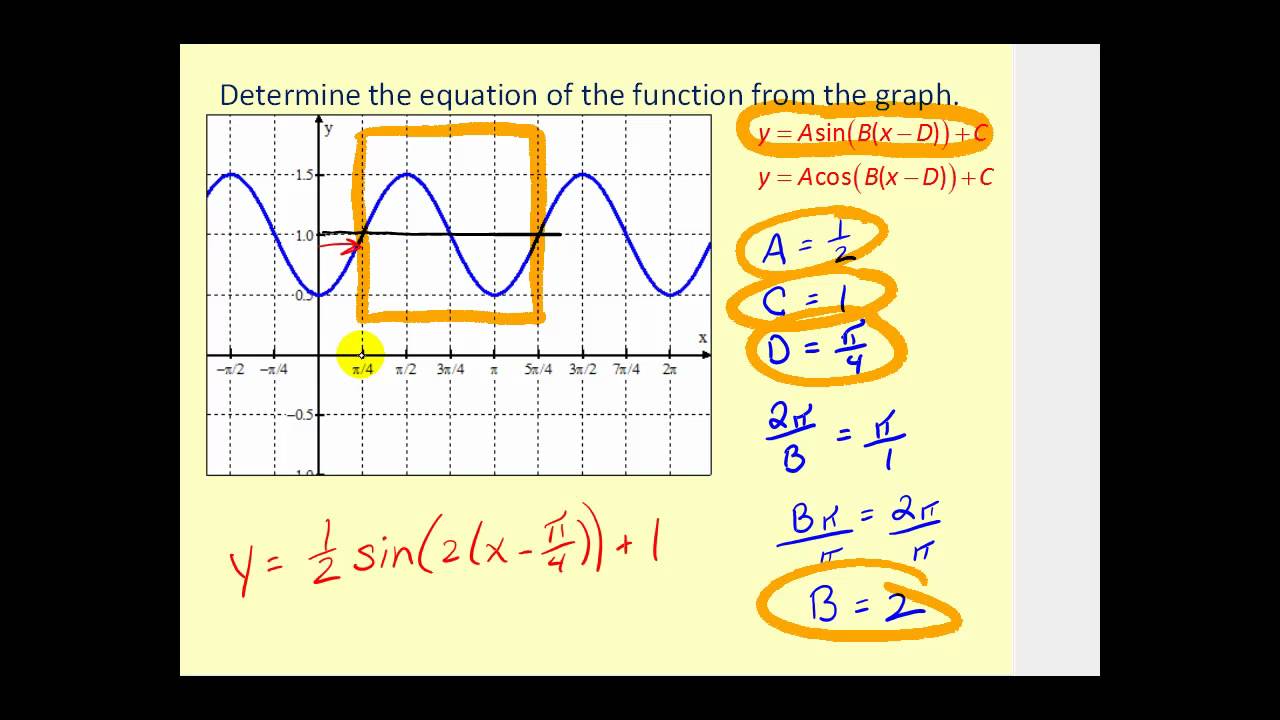
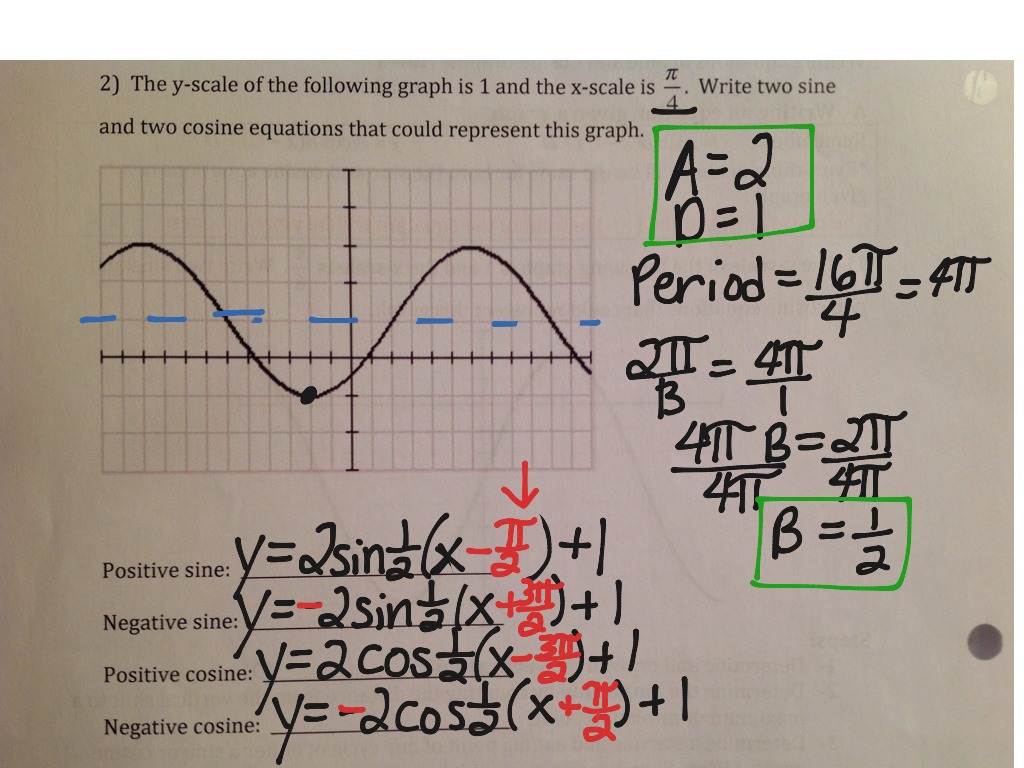
How To Write Sine Equation From Graph – How To Write Sine Equation From Graph
| Delightful to our website, in this period I’m going to teach you with regards to How To Clean Ruggable. And from now on, this is actually the initial impression:
Why don’t you consider picture previously mentioned? is actually which awesome???. if you think therefore, I’l l provide you with many impression yet again beneath:
So, if you desire to receive these wonderful pics about (How To Write Sine Equation From Graph), click on save link to save the pictures in your laptop. They’re available for transfer, if you appreciate and wish to obtain it, just click save symbol on the page, and it’ll be directly down loaded to your home computer.} Lastly if you wish to receive unique and recent photo related with (How To Write Sine Equation From Graph), please follow us on google plus or bookmark this blog, we try our best to present you regular update with fresh and new pictures. Hope you enjoy keeping right here. For some updates and latest news about (How To Write Sine Equation From Graph) images, please kindly follow us on tweets, path, Instagram and google plus, or you mark this page on book mark section, We attempt to provide you with update regularly with all new and fresh pics, love your surfing, and find the perfect for you.
Here you are at our website, articleabove (How To Write Sine Equation From Graph) published . Today we are excited to announce that we have found an awfullyinteresting contentto be discussed, namely (How To Write Sine Equation From Graph) Many individuals searching for info about(How To Write Sine Equation From Graph) and definitely one of them is you, is not it?