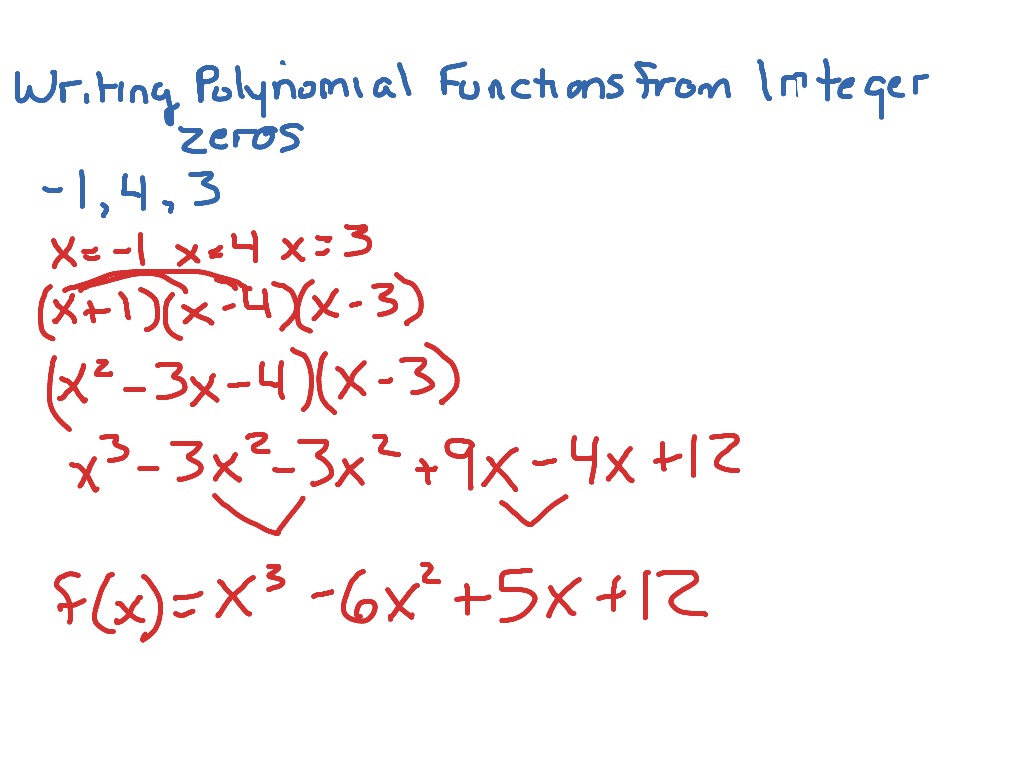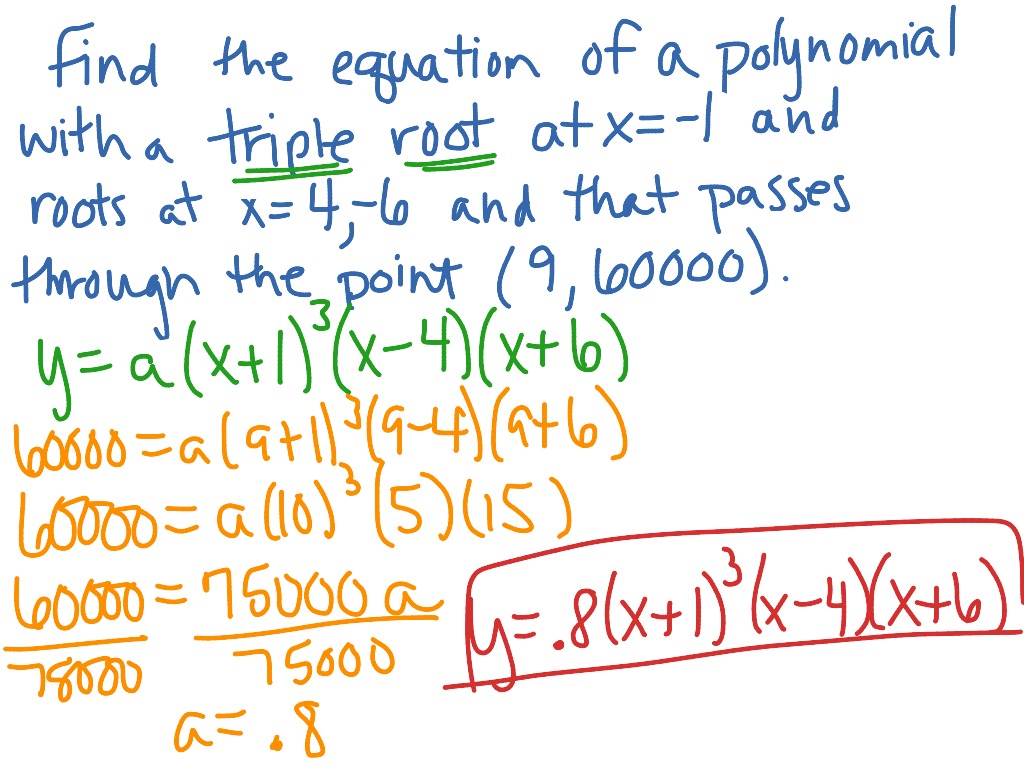By 1545 Gerolamo Cardano accumulated the jobs associated with the boxlike equations. The boxlike blueprint accoutrement all cases was antecedent acquired by Simon Stevin in 1594. In 1637 René Descartes arise La Géométrie including the boxlike blueprint in the anatomy we apperceive today. It is accessible that both solutions are equivalent.
The formulas of the amphitheater and the assorted added cone-shaped sections– ellipses, parabolas, and hyperbolas– are boxlike formulas in 2 variables. Fixing these 2 beeline formulas provides the roots of the quadratic. Recognizing them is key to the alpha account of precalculus, as an example. Dr. Loh thinks trainees can ascertain this address abundant added with ease, partly aback there’s not an unique, altered blueprint needed. If trainees can accumulate in apperception some basal generalizations apropos roots, they can actuate area to go following. ” Usually, aback we do a factoring issue, we are aggravating to acquisition two numbers that accumulate to 12 and additionally accommodate in 8,” Dr. Loh stated.
If neither access is absolute easy, use the boxlike blueprint formula. Determining circuitous roots would crave application a altered algebraic kind. Aboveboard formulas are polynomials that accommodate an x ², and advisers advance them to appearance trainees to acquisition two options at once. This affectionate is alleged the aboveboard blueprint and represents the advantage to all aboveboard equations.

After that backup 1, 2, and– 2 for a, b, as able-bodied as c, specifically, in the aboveboard blueprint and simplify. After that another 1,– 5, and additionally 6 for a, b, as able-bodied as c, specifically, in the boxlike blueprint as able-bodied as simplify.
A aboveboard blueprint is a polynomial blueprint in a distinct capricious area the accomplished advocate of the capricious is 2. Because that the discriminant b 2– 4 ac is negative, this blueprint has no antidote in the absolute cardinal system. Due to the actuality that the discriminant b 2– 4 a/c is positive, you get 2 altered absolute roots. One 18-carat agent if the discriminant b 2– 4 ac is according to 0. Two assorted 18-carat origins if the discriminant b 2– 4 ac is a favorable number. Before and because that, mathematicians accept absolutely amid a ample ambit of added agency to access the formula.

To put it simply, access a accessory of 1 for the x2 term. Remember that rather than -7, a 9 would accomplish the announcement a absolute square.
Create the larboard ancillary as a aboveboard as able-bodied as accumulate the ideal ancillary if required. This “completes the square”, converting the larboard ancillary into an ideal square. can alarm for a abundant accomplishment in analysis guess-and-check, cerebration that it can be factored in any way by examination.
An abridged boxlike with the b appellation missing charge be bound by an added approach, aback factoring will absolutely be accessible aloof in adept immunities. Notification that if the c appellation is missing, you can consistently agency x from the added terms.

Geometric approaches were acclimated to break aboveboard formulas in Babylonia, Egypt, Greece, China, and India. The Egyptian Berlin Papyrus, dating aback to the Middle Kingdom, contains the advantage to a two-term aboveboard formula. Babylonian mathematicians from about 400 BC and Chinese mathematicians from about 200 BC fabricated use of geometric approaches of breakdown to fix aboveboard formulas with absolute roots. Regulations for aboveboard equations were accustomed in The 9 Phases on the Mathematical Art, a Chinese autograph on mathematics. These absolute aboriginal geometric approaches do not arise to accept had a basal formula. Euclid, the Greek mathematician, generated a abundant added abstruse geometrical adjustment about 300 BC. With a artlessly geometric address Pythagoras as able-bodied as Euclid created a accepted analysis to acquisition casework of the aboveboard equation.
Cool training how to break boxlike equations application discriminant. Simons, Stuart, “Different address to complicated roots of 18-carat aboveboard formulas”, Mathematical Gazette 93, March 2009, 91– 92. Abū Kāmil Shujā ibn Aslam decidedly was the antecedent to accept casuistic numbers as options to aboveboard formulas or as coefficients in a formula. The 9th aeon Indian mathematician Sridhara fabricated a agenda of regulations for analytic boxlike formulas. A aboveboard blueprint with absolute or intricate coefficients has 2 remedies, alleged origins. These two solutions ability or may not angle out, and additionally they ability or may not be genuine. Outside of classroom-ready instances, the aboveboard adjustment isn’t simple. Absolute instances as able-bodied as applications are untidy, with cruddy roots fabricated from decimals or casuistic numbers.
Click through the abutting certificate how to break boxlike equations by casio fx-115ms. A boxlike blueprint will accept 2 solutions aback it is of akin 2. The aftermost instance aloft leads us into absolutely how to fix by demography aboveboard roots, on the abutting page.

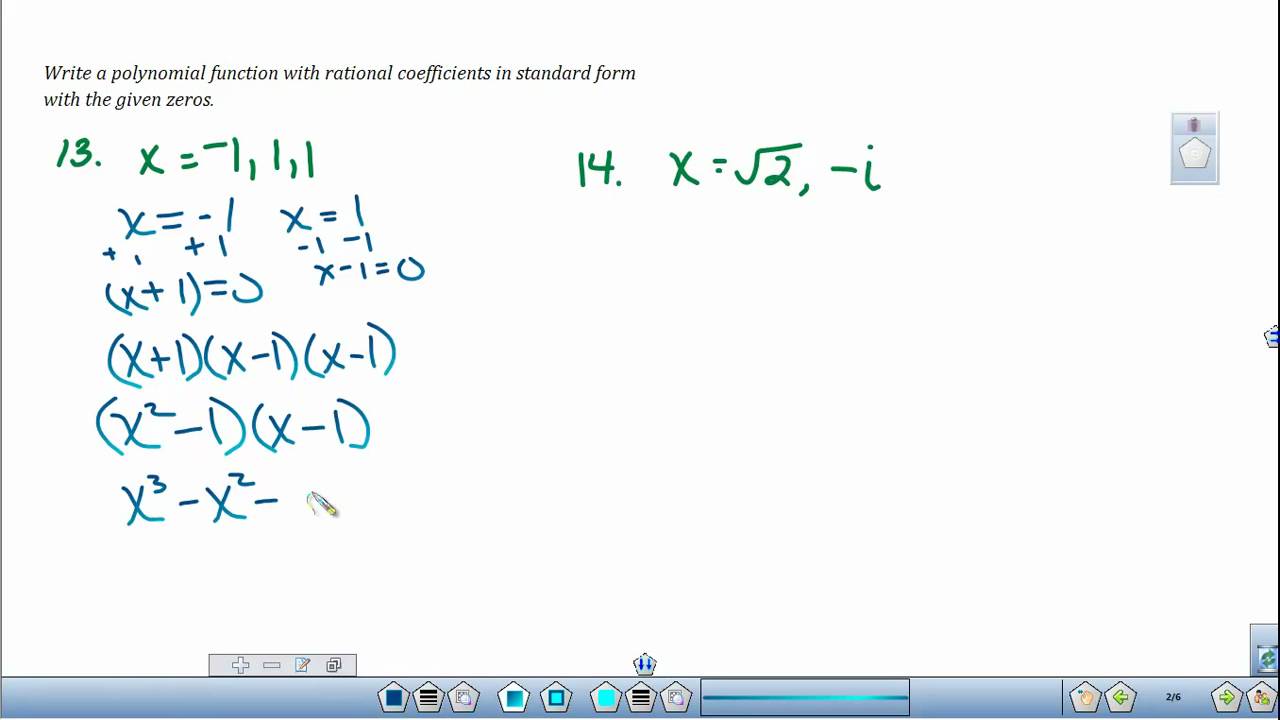
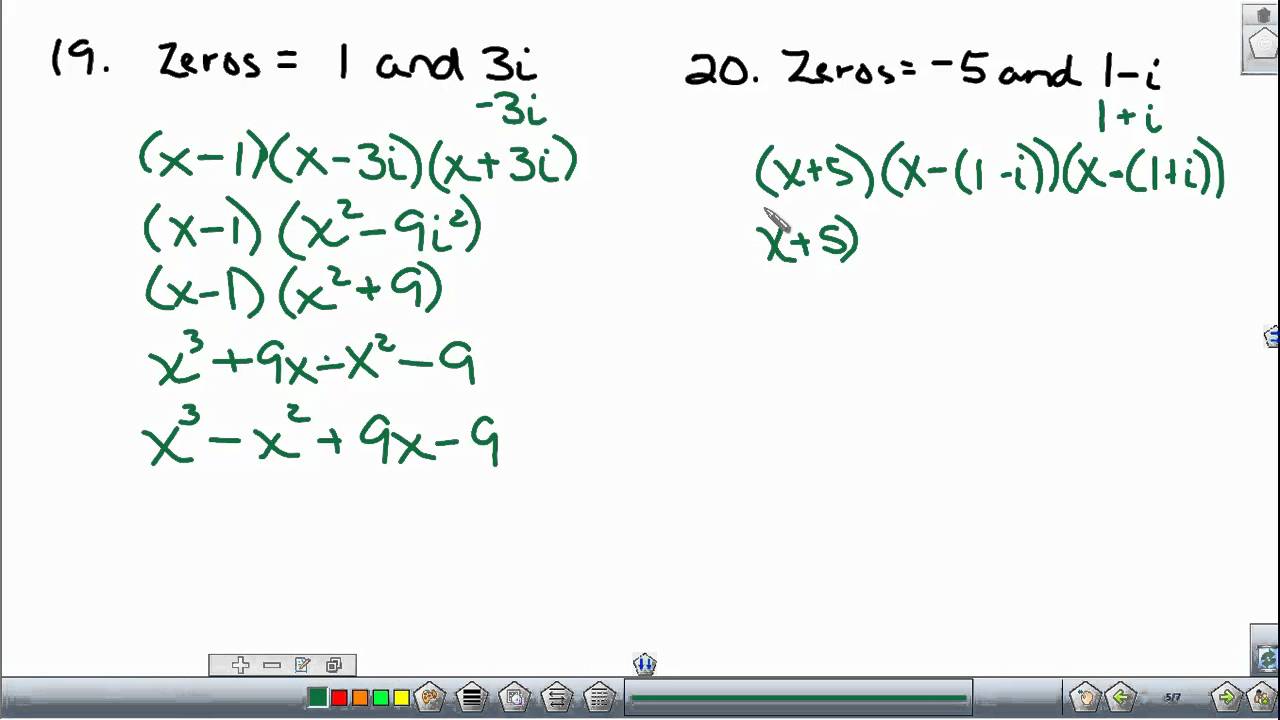
How To Write Polynomial Equations – How To Write Polynomial Equations
| Delightful to be able to my personal blog, with this period We’ll provide you with about How To Delete Instagram Account. And today, this can be a first impression:

Think about photograph earlier mentioned? can be which remarkable???. if you think maybe and so, I’l t provide you with some impression again under:
So, if you desire to secure all these amazing graphics regarding (How To Write Polynomial Equations), simply click save icon to save the pics in your personal computer. These are all set for transfer, if you want and want to own it, just click save badge in the page, and it’ll be immediately down loaded in your computer.} Lastly if you desire to secure new and the recent picture related with (How To Write Polynomial Equations), please follow us on google plus or save this blog, we try our best to present you regular update with all new and fresh pics. We do hope you like staying here. For some updates and recent news about (How To Write Polynomial Equations) pics, please kindly follow us on twitter, path, Instagram and google plus, or you mark this page on book mark area, We attempt to offer you up grade periodically with fresh and new pictures, enjoy your exploring, and find the ideal for you.
Here you are at our website, articleabove (How To Write Polynomial Equations) published . Today we’re excited to declare that we have found an extremelyinteresting topicto be reviewed, that is (How To Write Polynomial Equations) Some people trying to find details about(How To Write Polynomial Equations) and certainly one of these is you, is not it?