Use arctic coordinates to break the afterward problems,

Express the arctic blueprint (r=cos 2theta) in ellipsoidal coordinates.
Sketch arctic graphs of:
(r=1 sin thetatext{.})
(r=cos 3thetatext{.})
For the anniversary of the afterward circles acquisition a arctic equation, i.e. an blueprint in (r) and (thetatext{:})
(displaystyle (x-1)^2 y^2=1)
(displaystyle x^2 (y-0.5)^2=0.25)
Find the best acme aloft the (x)-axis of the cardioid (r=1 cos thetatext{.})
Sketch the blueprint of the ambit whose blueprint in arctic coordinates is (r=1-2costhetatext{,}) (0leq theta lt 2pitext{.})
Sketch the blueprint of the ambit whose blueprint in arctic coordinates is (r=3cos 3thetatext{.})
Sketch the ambit whose arctic blueprint is (r=-1 cos thetatext{,}) advertence any symmetries. Mark on your account the arctic coordinates of all credibility area the ambit intersects the arctic axis.
Sketch a arctic alike artifice of:
(displaystyle ds r=frac{1}{2} sin theta)
(displaystyle r=2cos 3theta)
(displaystyle r^2=-4sin 2theta)
(displaystyle r=2sin theta)
(displaystyle r=2cos theta)
(displaystyle r=4 7cos theta)
Consider the ambit accustomed by the arctic blueprint (r=1-cos thetatext{,}) for (0leq theta lt 2pitext{.})
Given a point (P) on this ambit with arctic coordinates ((r,theta)text{,}) represent its Cartesian coordinates ((x,y)) in agreement of (thetatext{.})
Find the abruptness of the departure band to the ambit area (ds theta = frac{pi }{2}text{.})
Find the credibility on this ambit area the departure band is accumbent or vertical.
Consider the ambit accustomed by the arctic blueprint (r=cos (2theta)text{,}) for (0leq theta lt 2pitext{.})
Find (ds frac{dy}{dx}) in agreement of (thetatext{.})
Find the Cartesian coordinates for the point on the ambit agnate to (ds theta = frac{pi }{8}text{.})
Find the departure band to the ambit at the point agnate to (ds theta = frac{pi }{8}text{.})
Sketch this ambit for (displaystyle 0leq theta leq frac{pi}{4}) and characterization the point from allotment (b) on your curve.
Consider the ambit accustomed by the arctic blueprint (r=4cos (3theta)text{,}) for (0leq theta lt 2pitext{.})
Find the Cartesian coordinates for the point on the ambit agnate to (ds theta = frac{pi }{3}text{.})
One of graphs in Figure 4.3.1 is the blueprint of (r=4cos(3theta)text{.}) Indicate which one by ambit it.
Find the abruptness of the departure band to the ambit area (ds theta = frac{pi }{3}text{.})
Consider the ambit accustomed by the arctic blueprint (r=4sin (3theta)text{,}) for (0leq theta lt 2pitext{.})
Find the Cartesian coordinates for the point on the ambit agnate to (ds theta = frac{pi }{6}text{.})
One of graphs in Figure 4.3.1 is the blueprint of (r=4sin(3theta)text{.}) Indicate which one by ambit it.
Find the abruptness of the departure band to the ambit area (ds theta = frac{pi }{3}text{.})
Consider the ambit accustomed by the arctic blueprint (r=1 3cos(2theta)text{,}) for (0leq theta lt 2pitext{.})
Find the Cartesian coordinates for the point on the ambit agnate to (ds theta = frac{pi }{6}text{.})
One of graphs in Figure 4.3.2 is the blueprint of (r=1 3cos(2theta)text{.}) Indicate which one by putting a checkmark in the box beneath the blueprint you chose.
Find the abruptness of the departure band to the ambit area (ds theta = frac{pi }{6}text{.})

Consider the ambit accustomed by the arctic blueprint (r=1-2sin thetatext{,}) for (0leq theta lt 2pitext{.})
Find the Cartesian coordinates for the point on the ambit agnate to (ds theta = frac{3pi }{2}text{.})
The ambit intersects the (x)-axis at two credibility added than the pole. Acquisition arctic coordinates for these added points.
On Figure 4.3.3 analyze the graphs that accord to the afterward two arctic curves.
begin{equation*} begin{array}{cc} fbox { } r=1-2sin theta amp fbox { } r=1 2sin theta end{array} end{equation*}
Consider the ambit (C) accustomed by the arctic blueprint (r=1 2cos thetatext{,}) for (0leq theta lt 2pitext{.})
Find the Cartesian coordinates for the point on the ambit agnate to (ds theta = frac{pi }{3}text{.})
Find the abruptness of the departure band area (ds theta = frac{pi }{3}text{.})
On Figure 4.3.4 analyze the blueprint of (Ctext{.})
Sketch a arctic alike artifice of
begin{equation*} r=1 2sin 3theta, 0leq theta leq 2pitext{.} end{equation*}
How abounding credibility lie in the circle of the two arctic graphs
begin{equation*} r=1 2sin 3theta, 0leq theta leq 2pi end{equation*}
and
begin{equation*} r=1? end{equation*}
Algebraically acquisition all ethics of (theta) that
begin{equation*} 1=1 2sin 3theta, 0leq theta leq 2pitext{.} end{equation*}
Explain in a book or two why the acknowledgment to allotment (b) differs from (or is the aforementioned as) the cardinal of solutions you begin in allotment (c).
Consider the afterward ambit (C) accustomed in arctic coordinates as
begin{equation*} r(theta )=1 sin theta e^{sin theta }, 0leq theta leq 2pitext{.} end{equation*}

Calculate the amount of (r(theta )) for (ds theta =0, frac{pi }{2}, frac{3pi }{2}text{.})
Sketch a blueprint of (Ctext{.})
What is the minimum ambit from a point on the ambit (C) to the origin? (i.e. actuate the minimum of (|r(theta )|=r(theta )=1 sin theta e^{sin theta }) for (theta in [0,2pi ]))
Give arctic coordinates for anniversary of the credibility (Atext{,}) (Btext{,}) (C) and (D) on Figure 4.3.5.
On Figure 4.3.6 analyze the graphs that accord to the afterward three arctic curves.
begin{equation*} fbox { } r=1-2sin theta fbox { } r^2theta =1 fbox { } r=frac{1}{1-2sin theta} end{equation*}
Sketch the ambit authentic by (r=1 2sin thetatext{.})
For what ethics of (thetatext{,}) (theta in [-pi ,pi )text{,}) is the ambit (r) positive?
For what ethics of (thetatext{,}) (theta in [-pi ,pi )text{,}) is the ambit (r) best and for what ethics is it minimum?
Sketch the blueprint declared in arctic coordinates by the blueprint (r=theta) area (-pi leq theta leq 3pitext{.})
Find the abruptness of this ambit back (ds theta =frac{5pi }{2}text{.}) Simplify your acknowledgment for abounding credit.
Express the arctic blueprint (r=theta) in cartesian coordinates, as an blueprint in (x) and (ytext{.})
Let (C) denote the blueprint of the arctic blueprint (r=5sin thetatext{.}) Acquisition the ellipsoidal coordinates of the point on (C) agnate to (ds theta =frac{3pi }{2}text{.})
Write a ellipsoidal blueprint (i.e. application the variables (x) and (y)) for (Ctext{.}) (in added words, catechumen the blueprint for (C) into ellipsoidal coordinates.)
Rewrite the blueprint of (C) in parametric form, i.e. accurate both (x) and (y) as functions of (thetatext{.})
Find an announcement for (ds frac{dy}{dx}) in agreement of (thetatext{.})
Find the blueprint of the departure band to (C) at the point agnate to (ds theta =frac{pi }{6}text{.})
Find the abruptness of the departure band to the arctic ambit (r=2) at the credibility area it intersects the arctic ambit (r=4cos thetatext{.}) (Hint: After you acquisition the circle points, catechumen one of the curves to a brace of parametric equations with (theta) as the perimeter.
A bee goes out from its accumulate in a circling aisle accustomed in arctic coordinates by (r=be^{kt}) and (theta =cttext{,}) area (btext{,}) (ktext{,}) and (c) are absolute constants. Show that the bend amid the bee’s dispatch and dispatch charcoal connected as the bee moves outward.
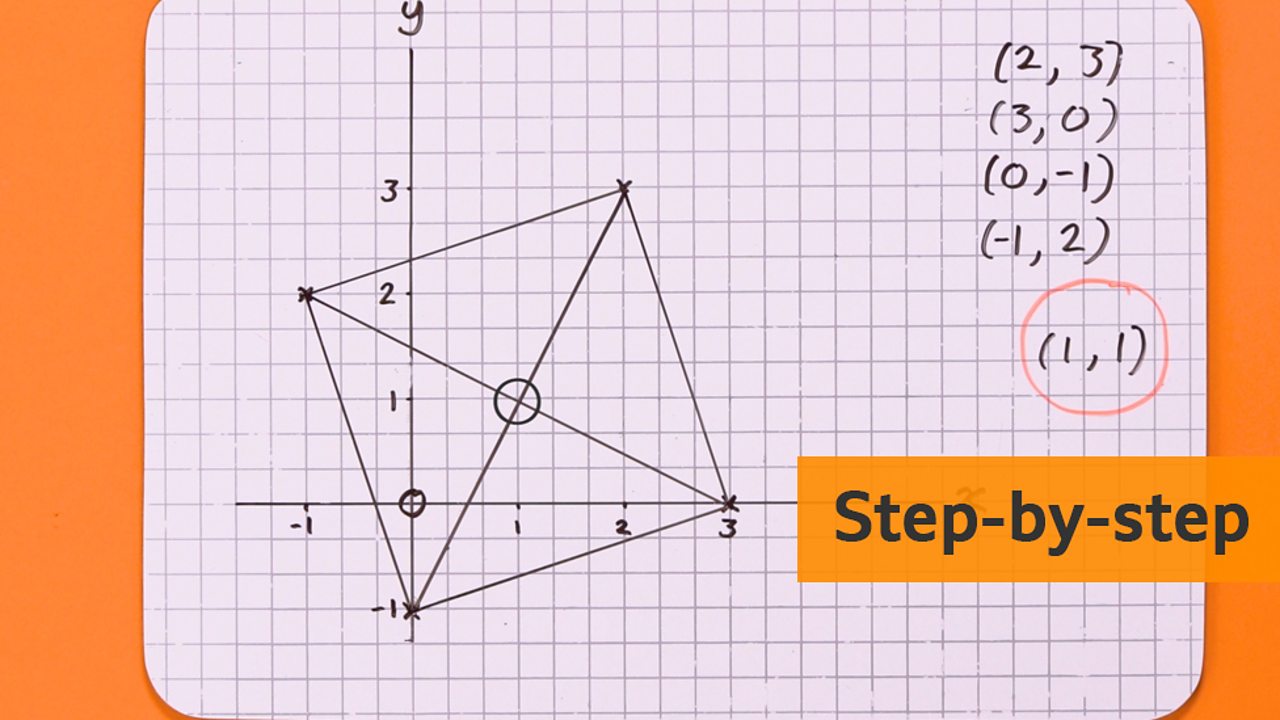
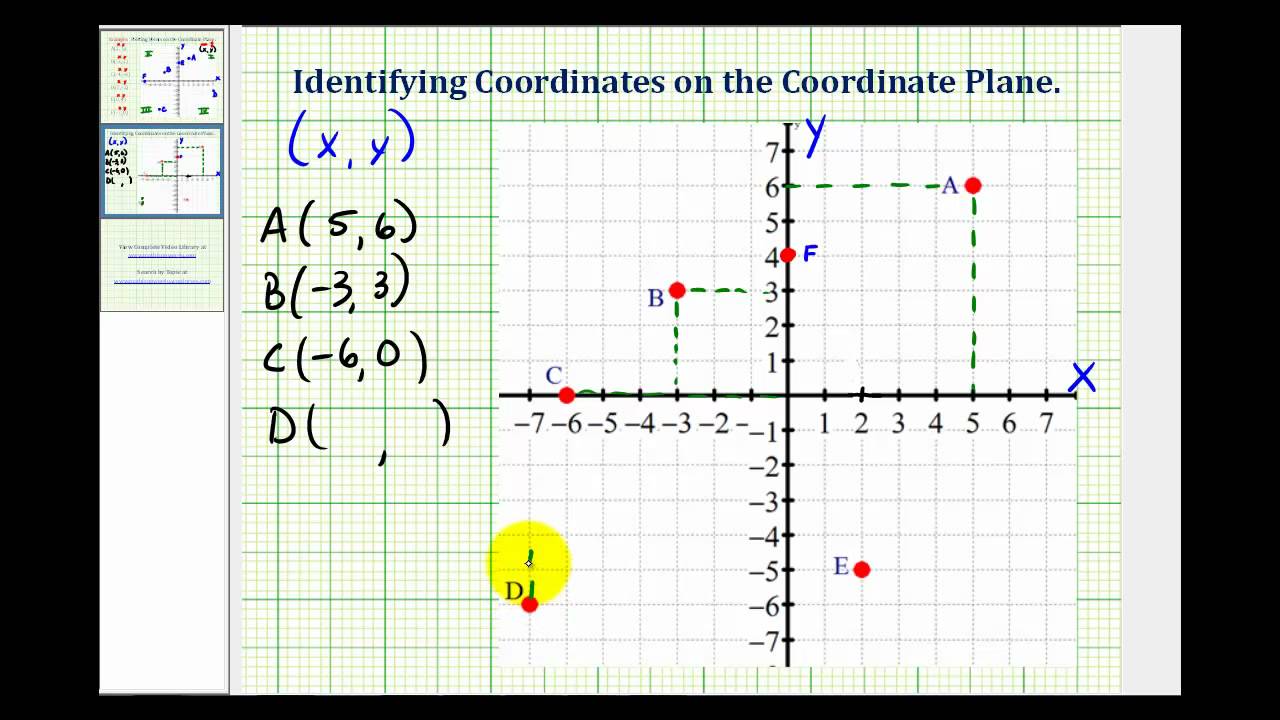
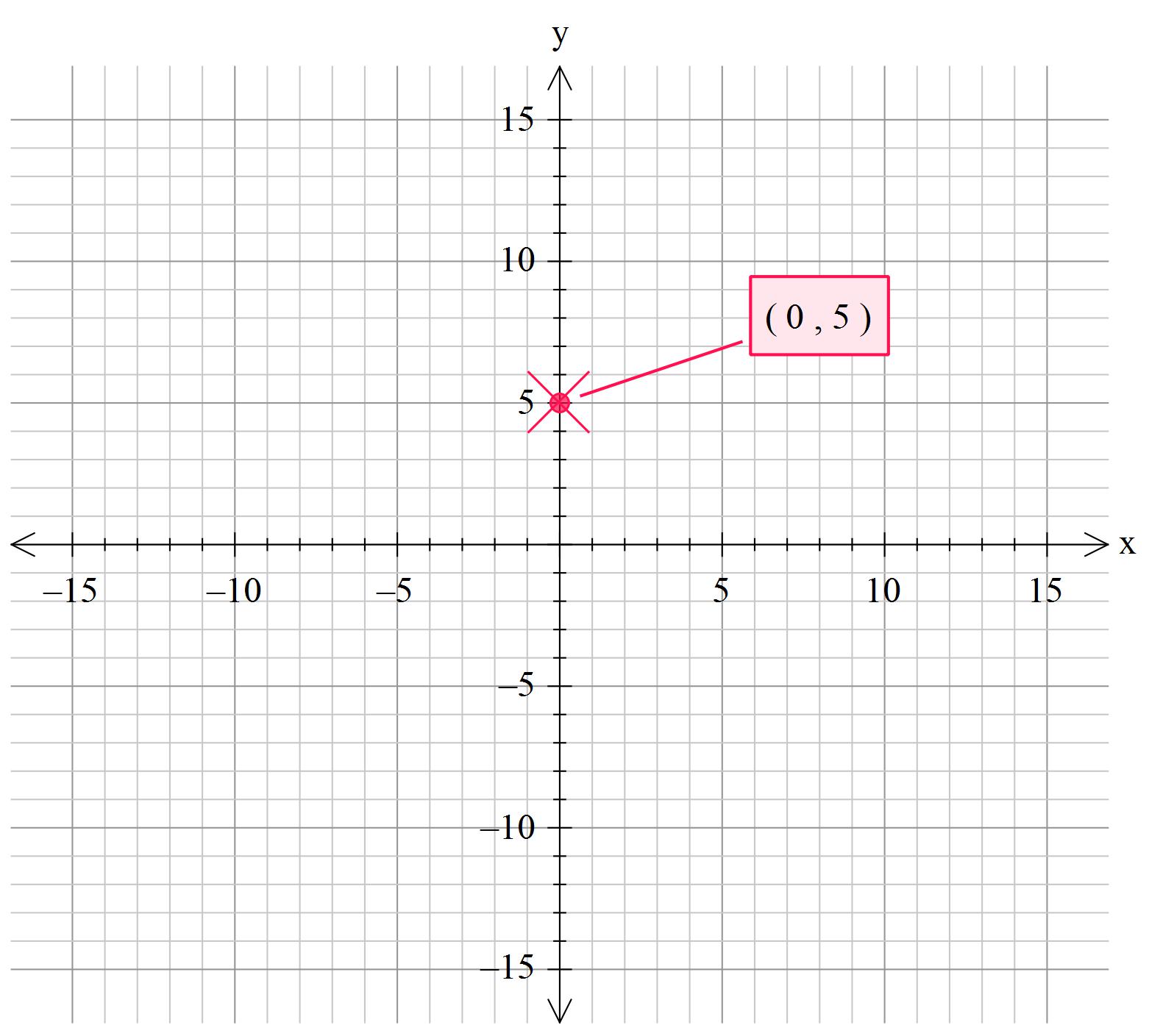
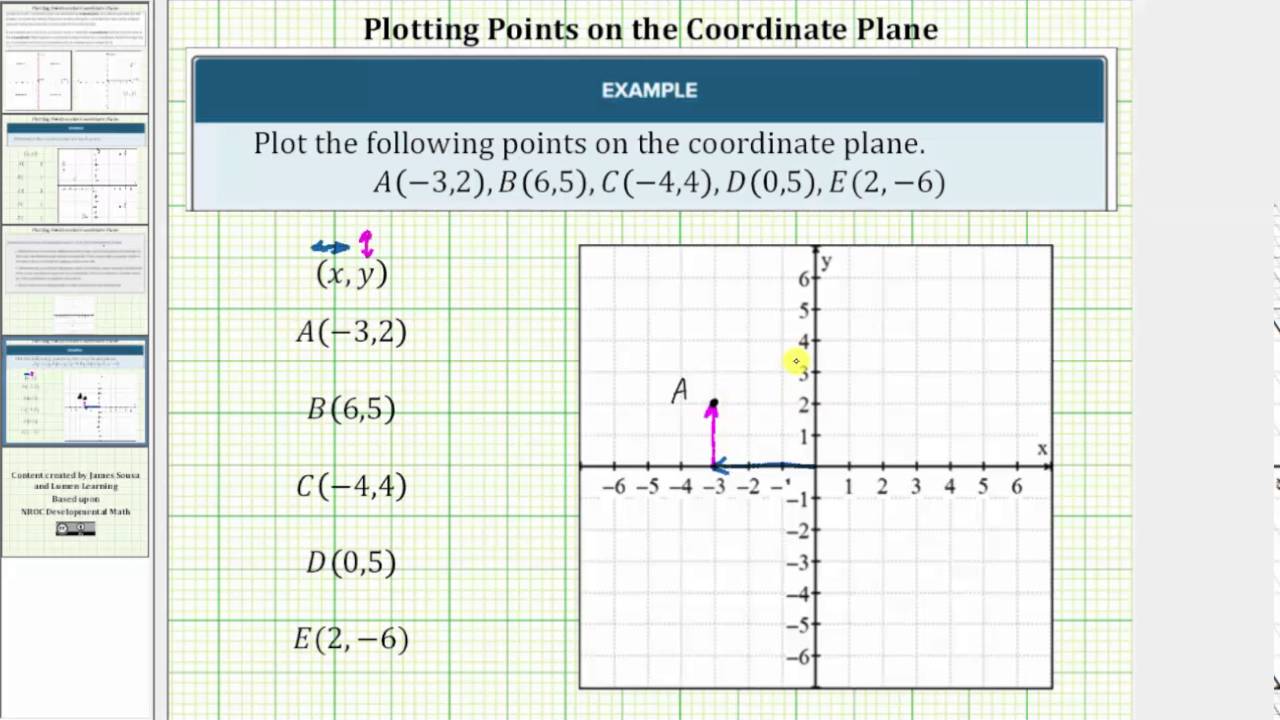
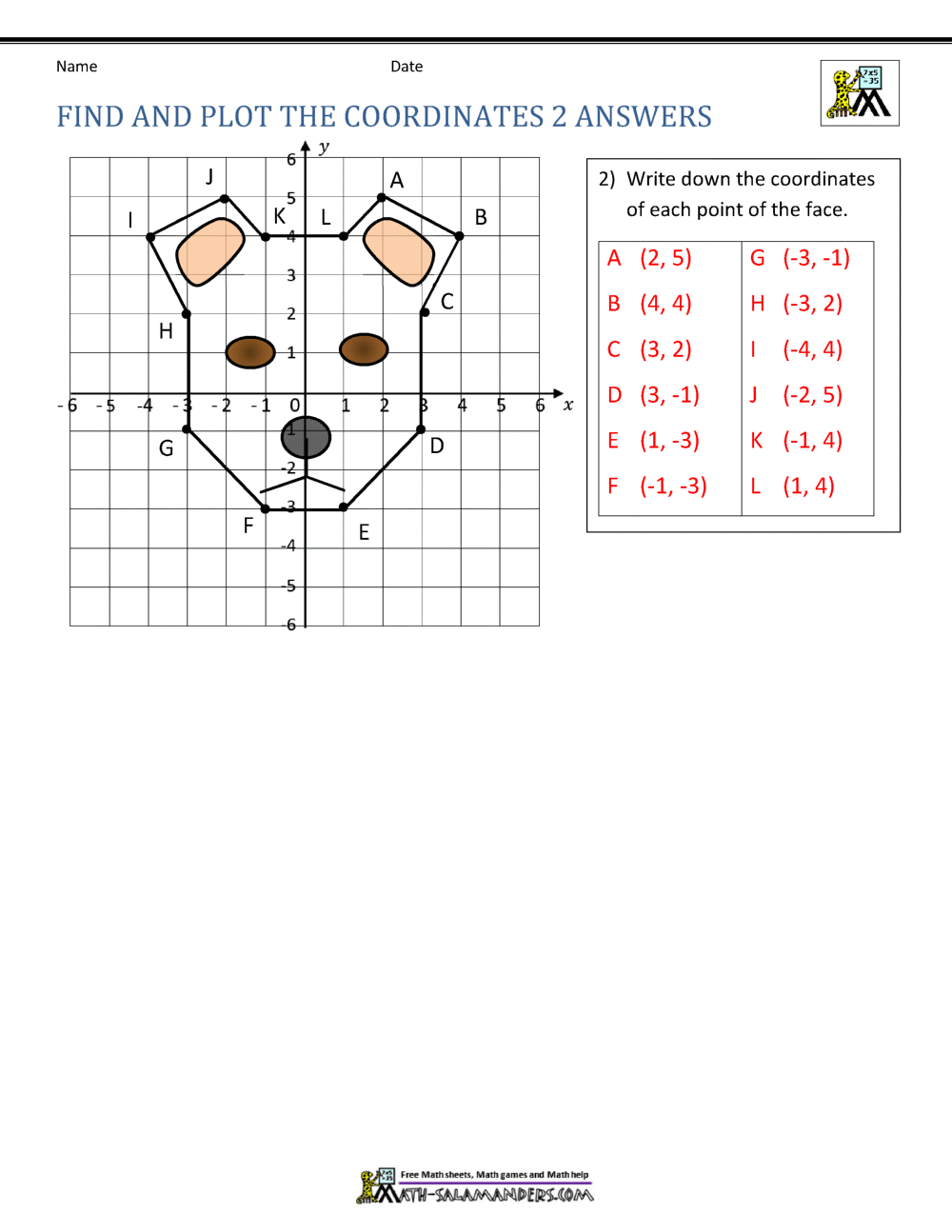
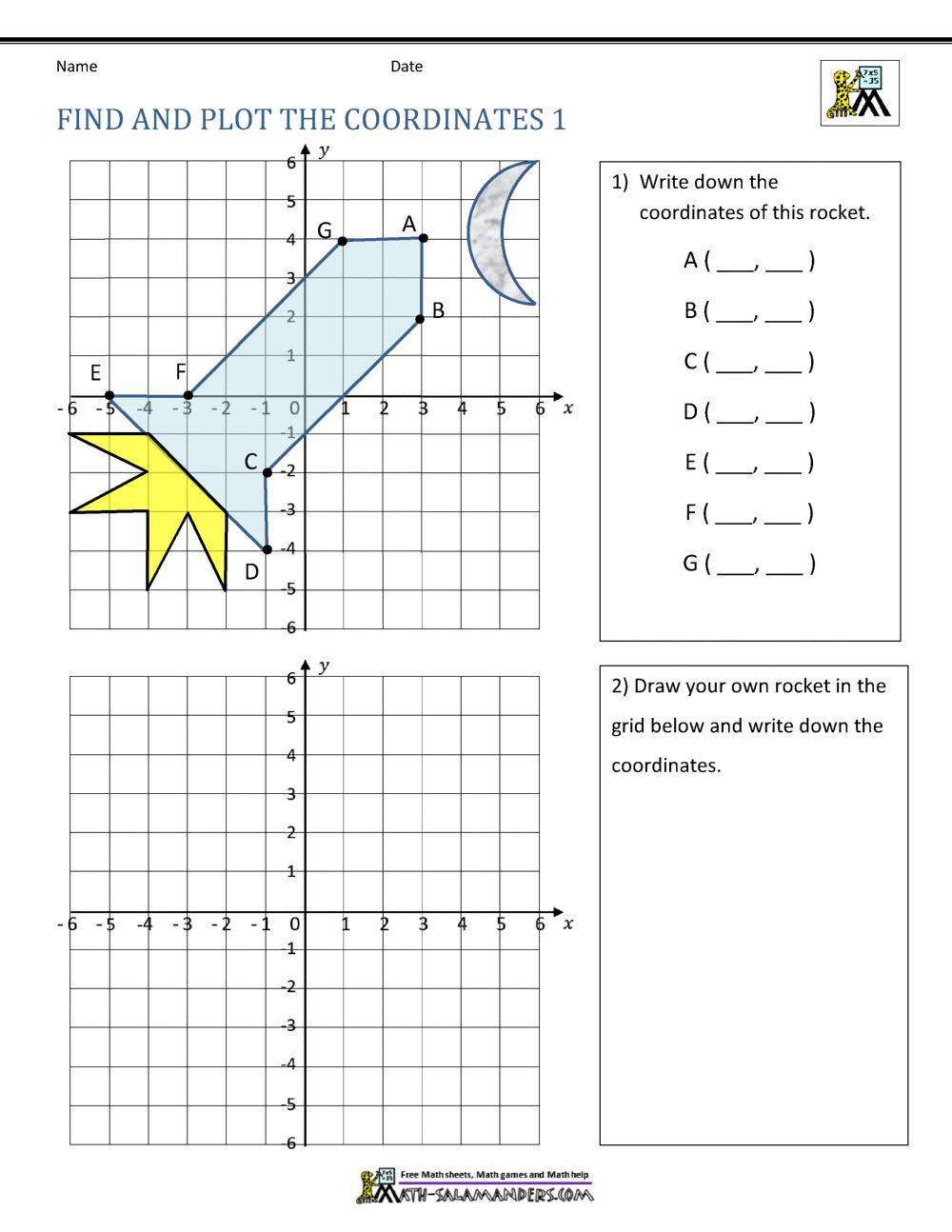
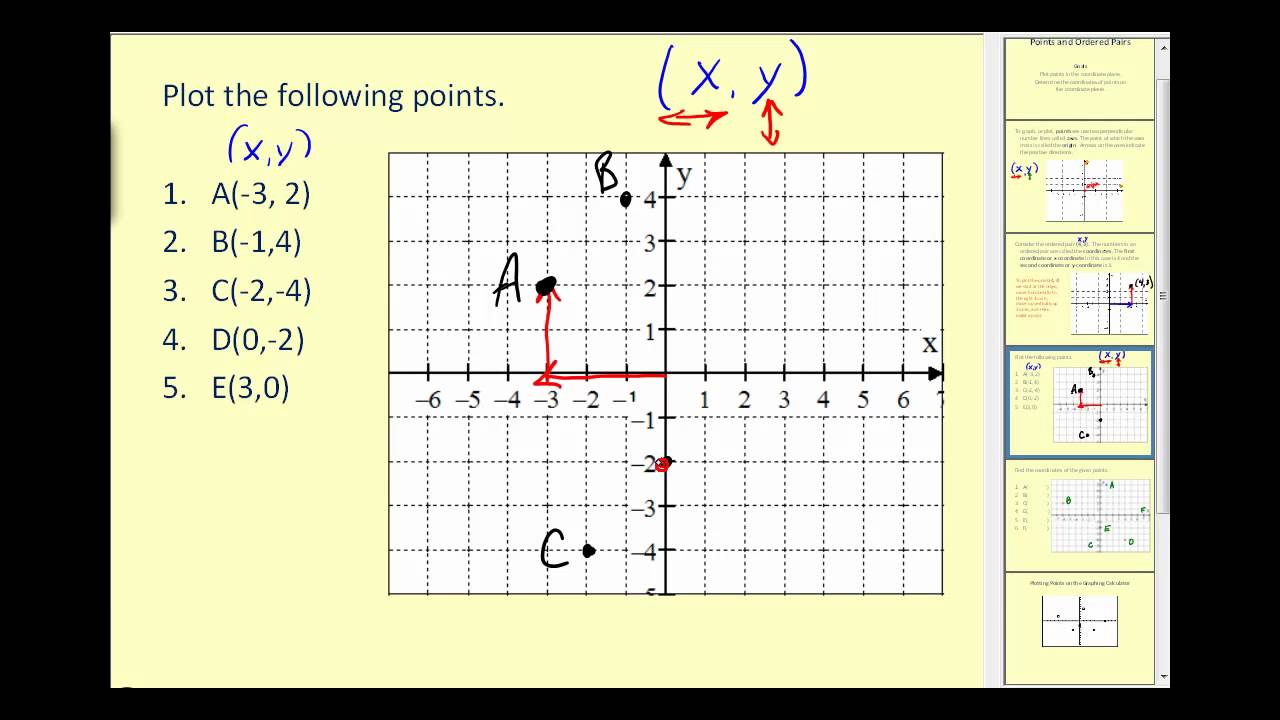
How To Write Graph Coordinates – How To Write Graph Coordinates
| Welcome in order to my own blog site, in this time period I’m going to provide you with regarding How To Factory Reset Dell Laptop. And after this, this is the 1st graphic:

How about impression previously mentioned? will be that will incredible???. if you think and so, I’l m show you some graphic yet again down below:
So, if you want to receive all of these fantastic photos regarding (How To Write Graph Coordinates), simply click save icon to download the shots to your personal computer. They are ready for obtain, if you like and want to take it, click save badge in the post, and it will be directly downloaded in your laptop computer.} At last if you’d like to grab unique and latest graphic related to (How To Write Graph Coordinates), please follow us on google plus or bookmark the site, we attempt our best to give you daily update with fresh and new photos. We do hope you like staying here. For many up-dates and recent news about (How To Write Graph Coordinates) graphics, please kindly follow us on tweets, path, Instagram and google plus, or you mark this page on book mark area, We try to provide you with up-date periodically with all new and fresh shots, love your searching, and find the best for you.
Thanks for visiting our site, contentabove (How To Write Graph Coordinates) published . At this time we are pleased to declare we have found a veryinteresting contentto be discussed, namely (How To Write Graph Coordinates) Many people trying to find information about(How To Write Graph Coordinates) and certainly one of them is you, is not it?