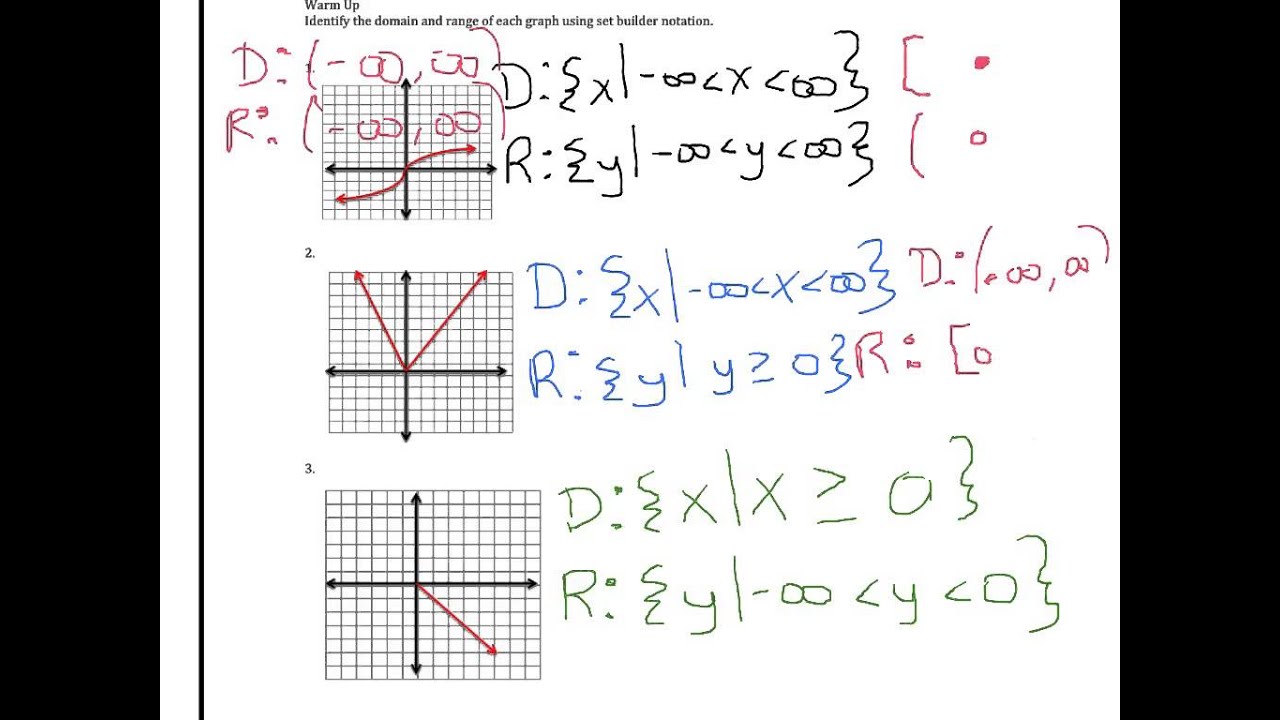Chapter 5: Probabilism and Induction

What acumen is there to acquire that the approaching will resemble the past, or that unobserved particulars will resemble empiric ones? None, of course, until resemblances are added specified, e.g., because we do not and should not apprehend the approaching to resemble the accomplished in annual of actuality past, nor do or should we apprehend the unobserved to resemble the empiric in annual of actuality observed. Appropriately Nelson Goodman replaces the old botheration (‘Hume’s’) of acknowledgment consecration by the new botheration of allegorical the respects in which resemblances are expectable amid accomplished and future, empiric and unobserved.
The old botheration is thereby postponed, not solved. As anon as the new botheration is solved, the old one returns, as a appeal for the accreditation of the solution: “What acumen is there to apprehend the future/unobserved to resemble the past/observed with annual to such- and- such dichotomies or anecdotic schemes or magnitudes?” The anatomy of the catechism is added adapted back we allocution in agreement of judgmental anticipation instead of all-or- none apprehension of resemblance, but the new botheration still waits, appropriately modified.
It seems to me that Hume did not affectation his botheration afore the agency were at duke to break it, in the probabilism that emerged in the additional bisected of the seventeenth century, and that we apperceive today primarily in the anatomy that Bruno de Finetti gave it in the decade from 1928 to 1938. The band-aid presented actuality (to the old and new problems at once) is about present in Chapter 2 of de Finetti’s ‘La prevision’ (1937), but he stops abbreviate of the aftermost step, alive in Chapter 3 to a altered array of solution, that uses the angle of exchangeability. At the end of this cardboard I shall analyze and adverse the two solutions, and say why I anticipate it is that de Finetti disregarded (or, anyway, silently aghast at) the band-aid that lay attainable to duke at the end of his Chapter 2.
In a nutshell: probabilism sees opinions as added or beneath absolute estimates of assorted magnitudes, i.e., anticipation abounding averages of fom
( I ) est X = xopo xl p1 . . .,
where the xi are the altered ethics that the aftereffect X can assume, and anniversary pi is the anticipation that the bulk absolutely affected is xi (If X is a connected magnitude, alter the sum by an integral.)
Estimation is not a bulk of aggravating to assumption the authentic value, e.g., 2.4 ability be an eminenty reasonable appraisal of the cardinal of someone’s children, but it would be a antic guess. (If that was my estimate, my assumption ability be 2.) Similarly, demography the accurateness bulk of a antecedent to be 1 or 0 depending on whether it is authentic or false, my appraisal of the accurateness bulk of the antecedent that I shall abide the present aeon is about 1/2, which couldn’t be the accurateness bulk of any proposition.
The anticipation you aspect to a antecedent is your appraisal of its accurateness value: if X is a proposition, then
(2) prob X = est X.
Here I chase de Finetti in demography propositions to be magnitudes that acquire the bulk 1 at worlds area they are true, and 0 area false. This comes to the aforementioned affair as the added accustomed identification of propositions with the sets of worlds at which they are true, and makes for accurateness here. Observe that (2) follows from (1), for as X can booty alone the two ethics 0 and 1, we can set xo = 0 and x1 = 1 in (1) to get
est X = 0po 1p1= p1
where pi is the anticipation that X assumes the bulk I, i.e., the anticipation (prob X) that X is true.
Still afterward de Finetti, I booty admiration to be the basal concept, and ascertain anticipation in agreement of it. (The adverse tack, with admiration authentic in agreement of anticipation as in (1), is added familiar.) Again (2) is accustomed the cachet of a definition, and the afterward axioms are adopted for the admiration operator.
(3) Additivity: est X Y = est X est Y
(4) Positivity: If X > 0 again est X > 0
(5) Normalization: est 1 = 1
(1 is the aftereffect that assumes the bulk 1 everywhere. i.e., the all-important proposition. ‘X > 0’ agency that X assumes abrogating ethics nowhere.)
Once understood, these axioms are as attainable as the laws of argumentation – – in badge of which actuality I shall alarm them and their after-effects laws of ‘probability logic’ (de Finetti’s ‘logic of the probable’). Actuality they are, in English:
(3) An appraisal of the sum of two magnitudes charge be the sum of the two abstracted estimates.
(4) An appraisal charge not be abrogating if the aftereffect estimated cannot be negative.
(5) If the aftereffect is absolutely I, the appraisal charge be 1 .
Additivity impliesl that for anniversary absolute cardinal k,
(6) est kX = k est X
The Kolmogorov axioms for anticipation are attainable after-effects of axioms (3)- (5) for estimation, calm with (2) as a notational convention, i.e.,
(7) If X can booty no ethics but 0 and I, again est X = prob X.
Here are the Kolmogorov axioms.
(8) Additivity: If XY= 0 again prob X Y = prob X prob Y
(9) Positivity: prob X>=0
(10) Normalization: prob 1 =1
(10) is aloof affected from the normalization adage (5) for est. with ‘est’ transcribed as ‘prob’. Positivity is the aforementioned for ‘prob’ as for ‘est’, accustomed that back we address ‘prob X’ it goes afterwards adage that X > 0, back a antecedent X can acquire no ethics but 0 and 1. And additivity of prob as aloft comes to the aforementioned affair as the added accustomed version, i.e.,
If X and Y are adverse propositions, prob X v Y = prob X prob Y.
(With 0 for canard and 1 for truth, the action XY = 0 that the artefact of X and Y be 0 everywhere comes to the aforementioned affair as analytic abhorrence of X and Y; and beneath the action XY = 0 the breach Xv Y, i.e., X Y – XY in the present notation, comes to the aforementioned affair as the simple sum X Y.)
A precise, complete appraisal apropos a accumulating of propositions would be represented by a anticipation action authentic on the accurateness anatomic cease of that collection. Added generally, a precise, complete appraisal apropos a accumulating of magnitudes ability be represented by an admiration abettor on the cease of that accumulating beneath the operations of accession and multiplication of magnitudes, and of multiplication of magnitudes by constants. (One ability additionally accommodate added options, e.g. cease beneath exponentiation, XY.)

Such are precise, complete opinions, according to probabilism. But for the best allotment our opinions run to blunder and incompleteness. Such opinions can be represented by altitude on the capricious ‘est’ or, equivalently, by the sets of authentic admiration operators that amuse those altitude Such sets will usually be convex, i.e., if the operators esto and est1 both accord to one, again so will the abettor woesto w1est1, if the w’s are non- abrogating absolute numbers that sum to 1. An archetype is accustomed by what de Finetti (1970, 1974 3.10) calls ‘The Axiological assumption of probability’:
Given a articular appointment of probabilities to a bound cardinal of propositions, the anticipation of any added propositions is either bent or can be coherently assigned any bulk in a assertive bankrupt interval.
Thus, the set of anticipation measures that accredit the accustomed ethics to the bound set of propositions charge be convex. And incomplete, estimated opinions can arise in added ways, e.g. in my book, The Argumentation of Decision (1965, 1983), a complete alternative baronial will frequently actuate an absolute set of anticipation measures, so that probabilities of propositions may be bent alone aural intervals: see 6.6, ‘Probability quantization’.
Probabilism would acquire you tune up your opinions with the aid of the anticipation calculus, or, added generally, the admiration calculus: anticipation logic, in fact. This is a bulk of archetype after-effects of altitude on admiration operators that accord to your opinion. Back you trace these after-effects you may acquisition that you had misidentified your opinion, i.e., you may see that afterwards all, the altitude whose after-effects you traced are not all such as you absolutely accept. Agenda that area your appraisal is abridged or imprecise, there is no admiration abettor you can alarm your own. Example: the action est(X– est X)2 <= 1 is not a action on your alien admiration operator, est. Rather: in that condition, ‘est’ is a variable, in agreement of which your appraisal can be articular with the set { est: est (X est X)2 <= 1 } of admiration operators that amuse it.
Here is the probabilistic band-aid that I promised, of the new botheration of induction. It turns on the breadth of the apprehension operator, in appearance of which we have
i.e., in words:
(11) An appraisal of the boilerplate of any (finite) cardinal of quantities charge according the boilerplate of the estimates of the abstracted quantities.
(Proof: use (6) to get 1/n out front, and again administer (3) n – 1 times.) From (11) we get what I shall alarm the
ESTIMATION THEOREM. If your appraisal apropos the magnitudes Xl,…,Xn, .. ,Xn m is characterized by the constraints est Xi = est Xj for all i, j = 1, …, n m (among added constraints, perhaps), again your appraisal of the boilerplate of the aftermost m of them will according the empiric boilerplate of the aboriginal n – if you apperceive that average, or anticipate you do.
Implicitly, this assumes that although you apperceive that the boilerplate of the aboriginal n X’s is (say) x, you don’t apperceive the alone ethics affected by Xl,…,Xn alone unless it happens that they are all absolutely x, for if you did, and they weren’t, the coercion est Xi = est Xj would not characterize your appraisal area the accepted bulk of Xi differs from the accepted bulk of Xj.
Proof of the admiration theorem. If you accredit anticipation I to the antecedent that the boilerplate of the aboriginal n X’s is x, again by (1)2 you charge appraisal that boilerplate as x The constraints again accord est Xi = x for the aftermost m X’s, and the cessation of the admiration assumption follows by (11).
Example 1: Academic weight
For connected magnitudes, estimates serve as guesses. Acquire that you will be adored if you assumption someone’s weight to aural an accurateness of one pound. One way to advance is to acquisition accession who seems to you to be of the aforementioned build, to be dressed similarly, etc., so that area X2 is the weight you ambition to assumption correctly, and Xl is the added person’s weight, your appraisal satisfies the coercion est X,=est X2. Now acquire the added being footfall on an authentic scale, and use that bulk of X, as your appraisal of X2. This is an appliance of the admiration assumption with n = m = 1.
Mind you: it is achievement of the coercion afterwards the acceptance that justifies (or amounts to) demography the added person’s absolute weight as your estimate, and beneath some circumstances, your appraisal ability change as a aftereffect of the acceptance so as to cease acceptable the constraint. Example: the added person’s weight ability prove to be so far from your apprehension as to attenuate your above-mentioned judgement that the two were relevantly similar, i.e., the base for your above-mentioned opinion’s achievement of the constraint. Actuality is a case area you had advanced advised the two bodies both to acquire weights in a assertive breach (say, from 155 to 175 pounds), so that back the added person’s weight accepted to be far alfresco this breach (perhaps, 120 pounds) your appraisal afflicted from {est: 155 <= est Xl = est X2< 175} to article else, because the acceptance imposed the added action est Xl = 120 on your opinion, i.e., a action adverse with the ahead accustomed ones. Anticipation argumentation charge not acquaint you how to alter your appraisal in such cases, any added than deductive argumentation charge acquaint you which of an inconsistent set of bounds to reject.
Example 2: Using averages as guesses
If you can acquisition (say) ten people, anniversary of whom strikes you as agnate in the accordant respects to an eleventh person, whose weight you ambition to guess, again acquire the ten accumulate on a ample belvedere scale, apprehend their absolute weight, and use a tenth of that as your appraisal of Xl1. This is an appliance of the admiration assumption with n = 10, m = 1. The admiration assumption does not endorse this appraisal as added authentic than one based on a distinct person’s weight, but beneath favorable altitude it may advice you anatomy an appraisal of your estimate’s accuracy, as follows.
Example 3: Variance
The about-face of a aftereffect X is authentic about to an admiration function:
var X = est (X – est X)2 = est X2 – est2 X.
Thus, about to an admiration action that characterizes your absolute opinion, the about-face of the eleventh person’s weight is your appraisal of the aboveboard of your absurdity in ciphering that weight, and this turns out to be according to the bulk by which the aboveboard of your appraisal of the aftereffect avalanche abbreviate of your appraisal of the aboveboard of the magnitude. Now the admiration assumption can be activated to the magnitudes Xl2, …, X2n l to authorize that beneath the constraints est Xi2 = est Xj2 for i, j = 1, …, n 1, your appraisal of the aboveboard of the eleventh person’s weight charge according the empiric boilerplate of the squares of the aboriginal ten people’s weights.3 To get the about-face of Xl1, artlessly decrease from that bulk the aboveboard of the appraisal of Xl1 formed in Archetype 2.
It is advantageous to arena the changes on these examples, e.g. apperception that you are ciphering weights not by eye, but on the base of cogent but bound statistical data, say, age and sex of the associates of the sample, and of the being whose weight is to be estimated; and apperception that it is not weight that is to be estimated, but breadth of activity – the appraisal of which has the accustomed name, ‘life expectancy’. (In this case the associates of the sample are apparently asleep already: bodies no adolescent than the one whose activity assumption is sought, who were relevantly agnate to that one, at that age).
The admiration assumption was aggressive by a chic of applications (in ‘La prevision’, Chapter 2) of what I shall call
DE FINETTI’S LAW OF SMALL NUMBERS: your appraisal of the cardinal of truths amid the propositions A1, …, An charge according the sum of the probabilities you aspect to them .
Here is accession formulation, acquired by adding both abandon of the blueprint by n and applying the breadth of est:
(12) Your appraisal of the about abundance of truths amid the propositions A1,…, An charge according the boilerplate of the probabilities you aspect to them.
Proof of de Finetti’s law. The affirmation is that est (Al . . . An) = prob Al . . . prob An, which is authentic by (3) and (7).
Example 4: Applying de Finetti’s law
To anatomy my probabilistic appraisal apropos the antecedent Al01 that the 101st bung of a assertive (possibly loaded) die will crop an ace, I calculation the cardinal of times the ace turns up on the aboriginal hundred tosses. Say the cardinal is 21, and acquire I don’t accumulate clue of the authentic tosses that yielded the aces. It is to be accepted that I aspect the aforementioned anticipation to all 101 propositions of anatomy Ai, i.e., it is to be accepted that my appraisal satisfies the constraints est Ai = estAj (i,j = 1, …,101). Again by de Finetti’s law with n = 100, the accepted bulk of those probabilities will be 21%, and that will be the anticipation of Al01 as well.
Observe that in the case of propositions, i.e., magnitudes whose alone attainable ethics are 0 and 1, the about-face is bent by the estimate, i.e., by the anticipation attributed to the proposition:
(13) If X is a antecedent of anticipation p, again var X = p(l – p).
Proof. As X is a proposition, X2 =X, and accordingly var X, in the anatomy est X2 – est2 X, can be accounting as est X – est2 X, i.e., p – p2, i.e., p(l – p). Thus, the about-face of a antecedent is absent back its anticipation is extreme: 0, or 1. And about-face is best (i.e., 1/4) back p is 1/2. You can see that allegedly by because that the attainable bulk of ‘p’ that is acute from both of the attainable ethics of X is the one absolutely in the middle.
These examples appearance how probabilism would acquire us anatomy our appraisal about the approaching on the base of accomplished experience, in simple cases of the actual sorts apropos which the botheration of consecration is frequently posed. The admiration theorem, and de Finetti’s laws of ample and baby numbers, are abnormally attainable genitalia of probabilism’s band-aid to the new botheration of consecration As the assumption and the law are after-effects of the axioms (3) (5) of anticipation logic, this band-aid can be apparent as borrowing its accreditation from those axioms. Appropriately the old botheration of induction, in the anatomy in which it bears on probabilism’s band-aid to the new problem, is the catechism of the accreditation of the axioms of anticipation logic.
Note that I say ‘probability logic’, not ‘logical probability’. De Finetti’s subjectivism implies that the basal axioms administering est (or, if you prefer, the agnate axioms for prob) are all the universally accurate attempt there are, for this logic. In contrast, Carnap (1950,1952, 1971, 1980) tentatively proposed added attempt as accepted validities for what he alleged ‘logical probability’, i.e., either a authentic anticipation function, e.g. c* (1945, 1950), or a chic of them, e.g. {c : 0 < < } (1952). But such attempts to analyze a adapted chic of one or added anticipation functions as the ‘logical’ ones bang me as hopeless. Example: the functions of anatomy c . do acquire absorbing backdrop that acclaim them for use as abstract anticipation functions in assertive sorts of cases, but there are affluence of added sorts of cases area none of those functions are suitable.4 Carnap (1980, 17) did see that, and assuredly added added adjustable parameters and, in an accomplishment to accomplish abounding generality. But I see no acumen to anticipate that would acquire been the end of the adorning process, had Carnap lived to abide it, or had others taken acceptable absorption in the activity to accompany it afterwards Carnap’s death5. With de Finetti, I booty the laws of anticipation argumentation to be the axioms (3)-(5) and their consequences6.

It seems adapted to alarm these axioms ‘logical’ because of the backbone and affection of their grip, as constraints that bang us as adapted for admiration functions. The feel of that anchor is like that of the anchor of such analytic laws (i.e., constraints on truth- bulk assignments) as that any proposition, X, implies its breach with any proposition, Y. In our notation, this comes out as X <= X Y – XY, accustomed that X and Y booty no ethics added than 0 and 1. I am at a accident to anticipate of added axiological attempt from which to deduce these axioms: to acquire is to acknowledge, accustomed what we acquire by ‘estimate.’
But this is not to abjure that illustrations can serve to highlight this analytic appearance of the axioms: a notable chic of such illustrations are the ‘Dutch book’ arguments, which advance by because situations in which your estimates of magnitudes will be the prices- in dollars at which you are accountable to buy or advertise (on demand) tickets that can be exchanged for numbers of dollars according to the authentic ethics of those magnitudes
Example. The Dutch book altercation for adage (3) goes like this, area x and y are the alien authentic ethics of the magnitudes X and Y. For definiteness, we accede the case area the adage fails because the left- duke ancillary is the greater. (If it fails because the left- duke ancillary is the smaller, artlessly altering ‘buy’ and ‘sell’ in the afterward argument, to appearance that you are accommodating to ache a abiding accident of est X est Y est (X Y).)
If est (X Y) exceeds est X est Y, you are accommodating to buy for est (X Y) dollars a admission annual x y dollars; and for a lower price, i.e., est X est Y dollars, you are accommodating to advertise a brace of tickets of that aforementioned accumulated worth: x y dollars. Thus, you are accommodating to ache a abiding loss, viz., est (X Y) – est X – est Y dollars.
To digest Brian Skyrms (1980, p. 119): if your estimates breach adage (3) in such cases, you are able to pay altered amounts for the aforementioned good, depending on how it is described. For a distinct admission annual x y dollars you will pay est (X Y) dollars, but for two tickets accordingly annual x y dollars you will pay a altered amount, i.e., est X est Y dollars. In a assertive bright sense, this is an inconsistency.
Such Dutch book arguments serve to highlight the accreditation of (3) (5) as axioms of the argumentation of estimation, i.e., of anticipation logic. One ability alike anticipate of them as demonstrating the apriori accreditation of the axioms, sc., as ‘logical’ truths in a assertive faculty beneath the antecedent that you are able to accomplish audible estimates of all the magnitudes that arise in them, in affairs area those estimates will be acclimated as your buying- or- affairs prices for tickets whose dollar ethics according the authentic ethics of those magnitudes. But the point of such demonstrations is blunted if one’s opinions are anticipation to be sets of admiration functions, or altitude on admiration functions, for again the antecedent that you are able to accomplish the audible estimates that the Dutch book arguments chronicle to will be annoyed alone in the acute cases area appraisal is absolute and complete, about to the magnitudes in question.
Even if you see the Dutch book arguments as alone suggestive, not demonstrative, you are absurd to cramp at the logicist band-aid to the old botheration of consecration ( 3) if you acquire the probabilistic band-aid floated in 2 for the new problem. But abounding will see probabilism as an evasion, not a solution; and while there can be no altogether absolute acknowledgment to such doubts, it would be ambiguous to end this cardboard afterwards some accomplishment to accommodated them.
The agnosticism can be illustrated able-bodied abundant in affiliation with Archetype 1: “Indeed, if you advance your antecedent opinion, according to which your estimates of the two people’s weights will be the same, the advice that one of them weighs (say) 132 pounds will aftermath a new appraisal in which both weights are estimated as 132 pounds. But to use your antecedent appraisal as a accomplishment in this way is to beg the catechism (“What shall your appraisal be?”) that the new botheration poses. It is alone by allurement that catechism that the old botheration can be askew as a appeal for the accreditation of the accepted constraints (3) (5) on all admiration functions, rather than for the adapted constraints that characterize your own opinion.”
That’s the catechism which a probabilist charge accountability as question- allurement in a artlessly objectivistic way. For that catechism contrasts your antecedent opinion, according to which est X1, = est X2, with the advice that the authentic bulk of X1, is 132. But what is appropriately aristocratic as ‘information’ is added carefully declared as a new affection of your opinion, authentic by two new constraints:
estX1 = 132, varX1 = 0
It is the additional of these that corresponds to the objectivistic assuming of the new estimate, 132, as information, not bald opinion. To adapt ‘information’ added acerb than this is to beg the catechism that the abettor answers (in effect) by basal his new appraisal in accordance with the new constraints: it is to say that his appraisal about X, is not alone audible (estX1 = 132) and assured (varX1 = 0) but correct.
In turn, objectivists will analyze this move as a archetypal subjectivistic abnegation to see the aberration amid abstract aplomb and cold warrant. “If the alone constraints that my appraisal charge accommodated are the basal axioms, I am chargeless to acquire any added constraints I please, as continued as they are consistent. But again I don’t charge to go through the business of award somebody who strikes me as agnate in build, weight of clothing, etc., to the being whose weight I ambition to guess, and acceptance that agnate person. I can artlessly adjudge on any cardinal at all (it ability alike be 132, as luck would acquire it), and use that as my guess: est X2 = 132. Nor does annihilation anticipate me from adopting abundant aplomb apropos that guess: var X2=0”. (Note that in Archetype 1, area var X1 was 0, there was no acumen to set var X2 = 0 as well.)
But this is nonsense, on a par with “If God is asleep again aggregate is permitted”. Look at it for a minute: God didn’t die, either aback or afterwards a continued illness. The antecedent is rather that there is no such entity, and never was. Our chastity has no all-powerful basis. Instead, its base is in us: it is as it is because and insofar as we are as we are. (‘Insofar as’: bodies are not as compatible as the all-powerful arrangement adventure suggests.) Moses banned the ten commandments up Mt. Sinai, in his heart. You apperceive the line.
I booty the aforementioned band about Carnap’s efforts, and Henry Kyburg’s, to acquaint us aloof what constraints on our probabilistic opinions would be rationally justified by this or that bulk of fully- captivated beliefs. If you anticipate that some such set of epistemological commandments charge be produced and justified if we are to anatomy acceptable probabilistic opinions, again you will acquisition subjectivistic probabilism offensively nihilistic: a authorization for ambitious cerebration and all added sorts of epistemological sin. But I anticipate such fears unwarranted. Ambitious cerebration is added frequently a affection of (shared or private) fantasy than of judgement. In basal appraisal we aim to the truth, for the best part. The actuality that I would be actionable no laws of argumentation if I were artlessly to adjudge on a cardinal out of the blue, as my appraisal of someone’s weight, does not beggarly that I would or could do that. (I could say ‘132’ or ‘212’ calmly enough, but could I acquire it?)
In a way, the adverse with von Mises’ frequentism is added anecdotic than that with Carnap’s logicism. Mises approved to authorize anticipation access as an absolute science, with its own subject- matter: accumulation phenomena. If that were right, there would be a accepted ability for free probabilities of all sorts: apropos horse races, the weather, U235–whatever. But according to the array of probabilism I am putting forward, such ability is topical: you go to altered bodies for your opinions about horse races, weather, U235 etc. Anticipation argumentation provides a accepted framework aural which all address of appraisal can be formulated, and tuned.
In the weight- academic archetype you are declared to acquire sought, and found, a being you saw as abundantly agnate in accordant respects to the one whose weight you admired to estimate, to actuate you that aural ample limits, any appraisal you anatomy for the one (e.g. by acceptance him on a calibration you trust) will be your appraisal for the added as well. Objectivism is accommodating to acquire your judgement that the authentic bulk of X1, is 132, based on the calibration reading, but rejects the allotment of your judgement that identifies the two estimates. But probabilism angle both scale- annual and equality-judging (for people’s weights) as acquired skills. (The aforementioned goes for anticipation the accurateness of scales.) The point about scale- annual is that it is a added broadly and analogously acquired skill, than is equality-judgement for people’s weights. But back it comes bottomward to it, your appraisal reflects your own appraisal of your own abilities of those sorts.
Here is how de Finetti (1938) bidding the basal attitude:
…one charge alter the roles of anterior acumen and anticipation theory: it is the closing that has free validity, admitting consecration is the acquired notion. One is appropriately led to achieve with Poincare that “whenever we acumen by consecration we accomplish added or beneath acquainted use of the calculus of probabilities”.
The aberration amid the access to the botheration of consecration that I advance actuality and the one de Finetti consort in ‘La prévision…’ is a aftereffect of the aberration amid de Finetti’s drive to accurate ambiguity by agency of audible anticipation or admiration functions (e.g. ‘exchangeable’ ones (1937) and ‘partially exchangeable’ ones (1938)), and the looser advance taken here, area opinions can be represented by constraints on admiration functions in cases area no one action abundantly represents the opinion. By demography this looser point of view,’ one can use the mathematically atomic admiration assumption to acquisition that beneath the constraints est X1 = . . . = est Xn m, empiric averages charge be acclimated as estimates of approaching averages, on affliction of incoherence, i.e., aberration with the canons of anticipation logic. In contrast, de Finetti (1937) uses the mathematically nontrivial law of ample numbers, according to which one’s amount of acceptance in the aberration amid any two averages’ beyond (say) 10-10 can be fabricated as baby as you like by authoritative the numbers of magnitudes Xi that arise in the averages both get ample enough. The coercion in de Finetti’s adaptation of the law of ample numbers are stronger than those in the admiration theorem: they crave actuality of absolute numbers a, b, c for which we have
estXi = a, est Xi2 = b, est(XiXj) = c
for all i, j = 1,2, … with i != j. (Only the aboriginal of these constraints applies to the admiration theorem, and again alone for i = 1, …,n m.)
I anticipate that de Finetti spurns or overlooks the admiration assumption because he insists on apery opinions by audible anticipation and admiration functions. He again uses conditionalization to booty acquaintance into account. As the accepted antecedent appraisal is absolute and complete, he gets not alone absolute estimates of averages in this way, but absolute variances, too . It is a arete of the admiration assumption that it uses a actual broadcast antecedent opinion, i.e., one that charge amuse no constraints but est X1 = . . . = est Xn m . There is no use of conditionalization in proving or applying the admiration theorem. If variances are forthcoming, it is by a added appliance of the admiration theorem, as in Archetype 3: empirically, in ample part8.
The affirmation is that through the admiration theorem, probabilism makes what ample faculty there is to be fabricated of aboveboard frequentism9, i.e., of Hume’s inductivism in its statistical atavar.
1. For absolute integers k, additivity acutely yields (6) by induction, back est(n 1)X=estX nX. Again for a absolute basal k, est(1/k)X=(1/k)estX, back kest(1/k)X=estX. This yields (6) for absolute rational k, beginning (6) follows for absolute absolute k by the body of the rationals in the reals. By (3) and (5), est 1 0 = 1 est0, so that back 1 0 = 1, (5) yields est 0 = 0 and, thus, (6) for k = 0. Finally, to get (6) for abrogating absolute k it suffices to agenda that est – 1 = – 1 back 0 = est 1 – 1 = 1 – est – l by (3) and (5). Actuality we acquire declared that for absolute a and b, est aX b Y is authentic whenever est X and est Y are, i e., we acquire affected that the area on which est is authentic is bankrupt beneath accession and beneath multiplication by reals.
2 (1) is deducible from (3), (6), and (7) in case X assumes alone finitely abounding altered ethics xi, for again we acquire X= vixSXs area Xi is the antecedent that X = xi, i.e., Xi assumes the bulk 1 (0) at worlds area X is authentic (false).
3 The constraints est Xi2 = est Xj2 represent a judgement absolutely altered from that represented by the constraints est Xi = est Xj a judgement we are beneath apt to make, or to feel assured of, accepting fabricated it. (Note that ciphering x 2 is not about aloof a bulk of squaring your appraisal of X!)
4 As Johnson (1932) showed, and Kemeny (1963) rediscovered, the cases area one of the functions cx is acceptable are absolutely those in which the user takes the adapted amount of acceptance in the abutting item’s acceptance to corpuscle Pi Of the administration {P1, …,Pk} to depend alone on (i) the cardinal of items already sorted into beef of that partitioning, and (ii) the cardinal amid them that acquire been assigned to corpuscle Pi.
5 Not anybody would accede that cipher is continuing assignment on Carnap’s project, e.g. Costantini (1982) sees himself as accomplishing that. But as I see it, his affairs – a actual absorbing one – is actual altered from Carnap’s.
6 There are two added axioms, which de Finetti does not acknowledge: an adage of continuity, and an adage that Lewis (1980) calls ‘The Principal Principle’ and others alarm by added names: prob (H 1 adventitious H = x ) = x, area adventitious H is the cold adventitious of H’s truth. De Finetti additionally omits adage (5), apparently on the arena that the estimates of magnitudes are to represent estimates of the utilities you apprehend from them, area the estimated account est X charge not be abstinent in the aforementioned units as X itself, e.g. area X is assets in florins, est X ability be abstinent in dollars.
7 I accumulate that it originates with Keynes (1921), reappears with Koopman (1940), and is accustomed about the anatomy acclimated actuality by Acceptable (1950, e.g. p. 3). It is consort by Levi (1974,1980) as allotment of a analytic program. I aboriginal encountered it, or article like it, in Kyburg (1961), but it took me 20 years to see its merits. Amid statisticians, the capital abutment for this way of apery estimated or abridged appraisal comes from Acceptable (1950, 1962), Smith (1961), Dempster (1967, 1968), and Shafer (1976). In practice, the business of acumen in agreement of a variable, prob’ or ‘est’, that satisfies assertive constraints, is boundless – but with an unsatisfactory rationale, according to which one is acumen about an unknown, audible function, which the capricious denotes.
8 Anyway, in beyond allotment than in de Finetti’s approach. Use of the empiric boilerplate is accepted to both, but the added constraints on est are weaker in this access than in de Finetti’s. Observe that with the symmetric collapsed above-mentioned anticipation action (Carnap’s C#), conditioning on the antecedent that m of the aboriginal n trials acquire been successes yields a after anticipation action prob about to which we consistently acquire prob X1 = . . . = prob Xn = m/n, but acquire prob Xn 1 = (m 1)/(n 2) m/n unless n = 2m. The case is agnate for added nonextreme symmetric priors, e.g. for all of form
9 Not von Mises’ science of attached about frequencies in aberrant collectives, but the prior, believable intuition.
References
Carnap, R.: 1945, ‘On anterior logic’, Philosophy of Science 12, 72 97.
Carnap, R.: 1950, Analytic Foundations of Probability, Univ. of Chicago Press.
Carnap, R.: 1952, The Continuum of Anterior Methods, Univ. of Chicago Press.
Carnap, R.: 1971, ‘A basal arrangement of anterior logic’, in Carnap and Jeffrey (eds.) (1971) and Jeffrey (ed.) (1980).
Carnap, R. and R. Jeffrey: 1971, Studies in Anterior Argumentation and Probability, Vol. 1, Univ. of California Press.
Costantini, D: 1982, ‘The role of anterior argumentation in statistical inference’, to arise in Proceedings of a Conference on the Foundations of Statistics and Probability, Luino, September 1981.
Dempster, Arthur P.: 1967, ‘Upper and lower probabilities induced by a multivalued mapping’, Annals of Mathematical Statistics 38, 395 339.
Dempster, Arthur P.: 1968, ‘A generalization of Bayesian inference’, J. Royal Stat. Soc., Series B. 30, 205 247.
Finetti, Bruno de: 1937, ‘La prevision: ses lois logiques, ses sources subjectives’, Annales de l’lnstitut Henri Poincare 7, 1- 68. (English adaptation in Kyburg and Smokler.)
Finetti, Bruno de: 1938, ‘Sur la action d’equivalence partielle’, ActualEites Scient. et Industr., No. 739, Hermann & Cie., Paris. (English adaptation in Jeffrey (1980).)
Finetti, Bruno de: 1970, 1974, TeoHa Della Probabditai, Torino; English translation, Access of Probability, Vol. 1, Wiley, New York. (Vol. 2, 1975).
Good, I. J.: 1950, Anticipation and the Acceptance of Evidence, Griffin, London.
Good, I. J.: 1962, ‘Probability as the admeasurement of a non- assessable set’, in Ernest Nagel, Patrick Suppes, and Alfred Tarski (eds.), Logic, Methodology, and Philosophy of Science: Proceedings of the 1960 International Congress, Stanford Univ. Press. Reprinted in Kyburg and Smokler.
Goodman, N.: 1979, Fact, Fiction and Forecast, Hackett Publ. Co., Indianapolis.
Hume, D.: 1739,A Treatise of Human Nature, London.
Jeffrey, Richard C.: 1965, 1983, The Argumentation of Decision, McGrawHill; 2nd ed., Univ of Chicago Press.
Jeffrey, Richard C.: 1980 (ed.), Studies in Anterior Argumentation and Probability, Vol. 2, Univ. of California Press.
Johnson, W. E.: 1932, ‘Probability’, Mind 41, 1- – 16, 281- 296, 408 423.
Kemeny, J: 1963, ‘Carnap’s access of anticipation and induction’, in P. A. Schilpp (ed.), The Philosophy of Rudolf Carnap, La Salle,111.
Keynes, John M.: 1921,A Treatise on Probabdity, London.
Kolmogorov, A. N.: 1933, Grundbegriffe der Wahrscheinlich-keitsrechnung, Ergebnisse der Msth., Band II, No. 3. (English Translation, Chelsea, N.Y., 1946.)
Koopman, B O.: 1940, ‘The bases of probability’, BuGetin of the American Mathematical Society 46, 763 774. Reprinted in Kyburg and Smokler.
Kyburg, Henry E., Jr.: 1961, Anticipation and the Argumentation of Rational Belief, Wesleyan Univ . Press, 1961.
Kyburg, Henry E., Jr. and Howard Smokler (eds.): 1980, Studies in Abstract Probability, 2nd ed., Krieger Publ. Co., Huntington, N.Y.
Levi, I.: 1974, ‘On general probabilities’, J. Phd. 71, 391418.
Levi, I.: 1980, The Enterprise of Knowledge, MIT Press.
Lewis, David K.: 1980, ‘A subjectivist’s adviser to cold change’, in Jeffrey (ed.) (1980).
Mises, Richard v.: 1919, ‘Grundlagen der Wahrscheinhchkeitsrechnung’, Math. Zs. 5.
Skyrms, B.: ‘Higher adjustment degrees of belief’, in D. H. Mellor (ed.), Prospects for Pragmatism, Cambridge Univ. Press
Shafer, G.: 1976, A Mathematical Access of Evidence, Princeton Univ. Press.
Smith, C. A. B.: 1961, ‘Consistency in statistical inference and decision’. Royal Stat. Soc., Series B. 23,1 25.
Dept. of Philosophy
Princeton University

Princeton, N.J. 08544, U.S.A.
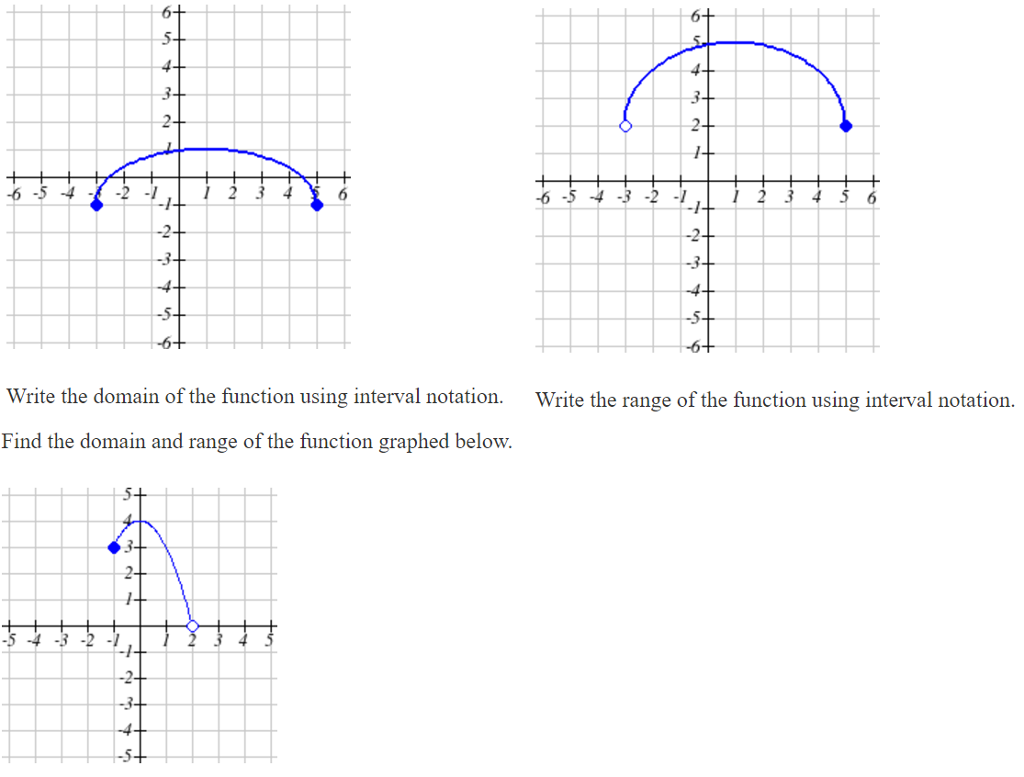
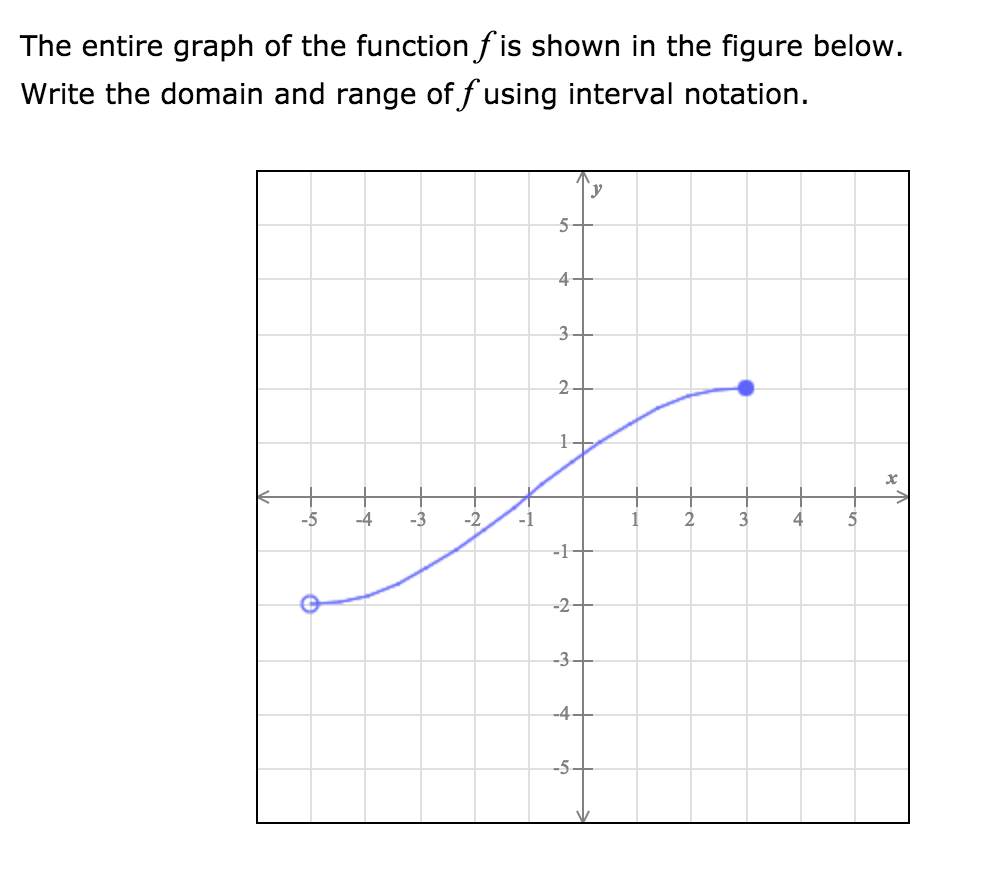
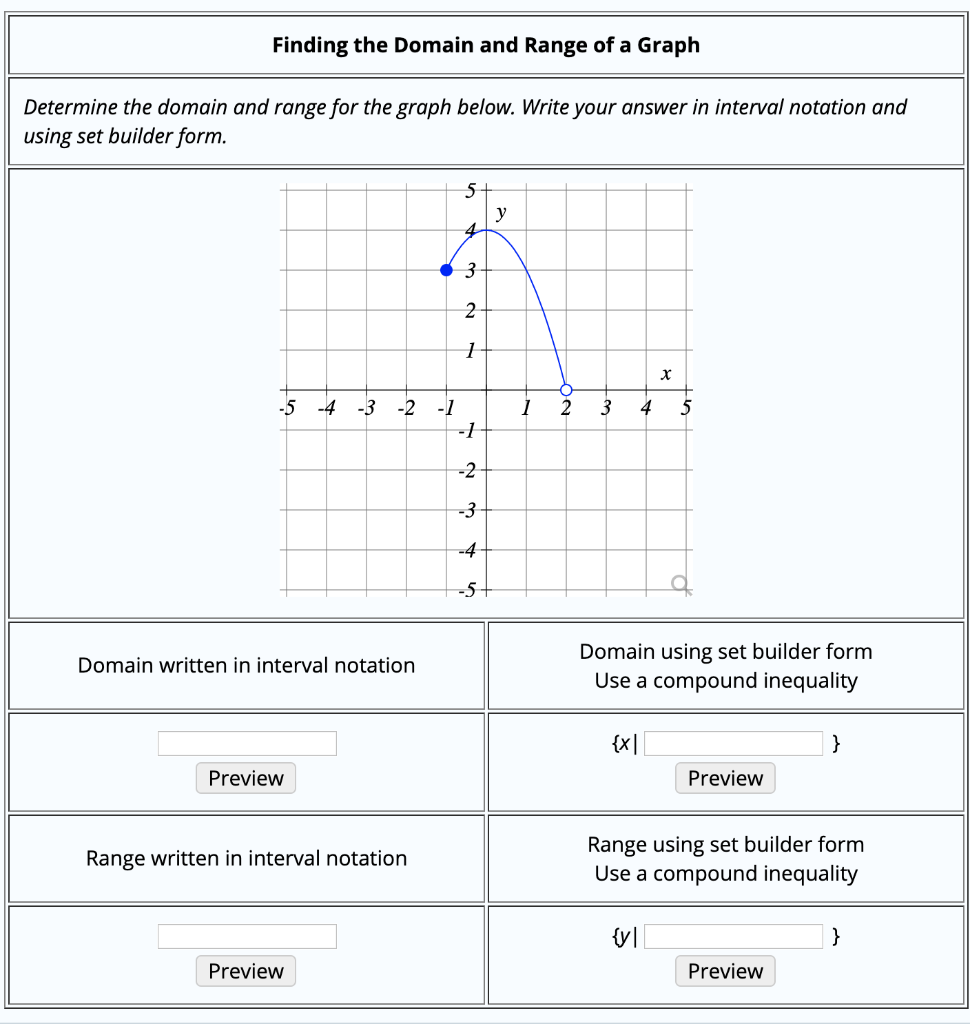
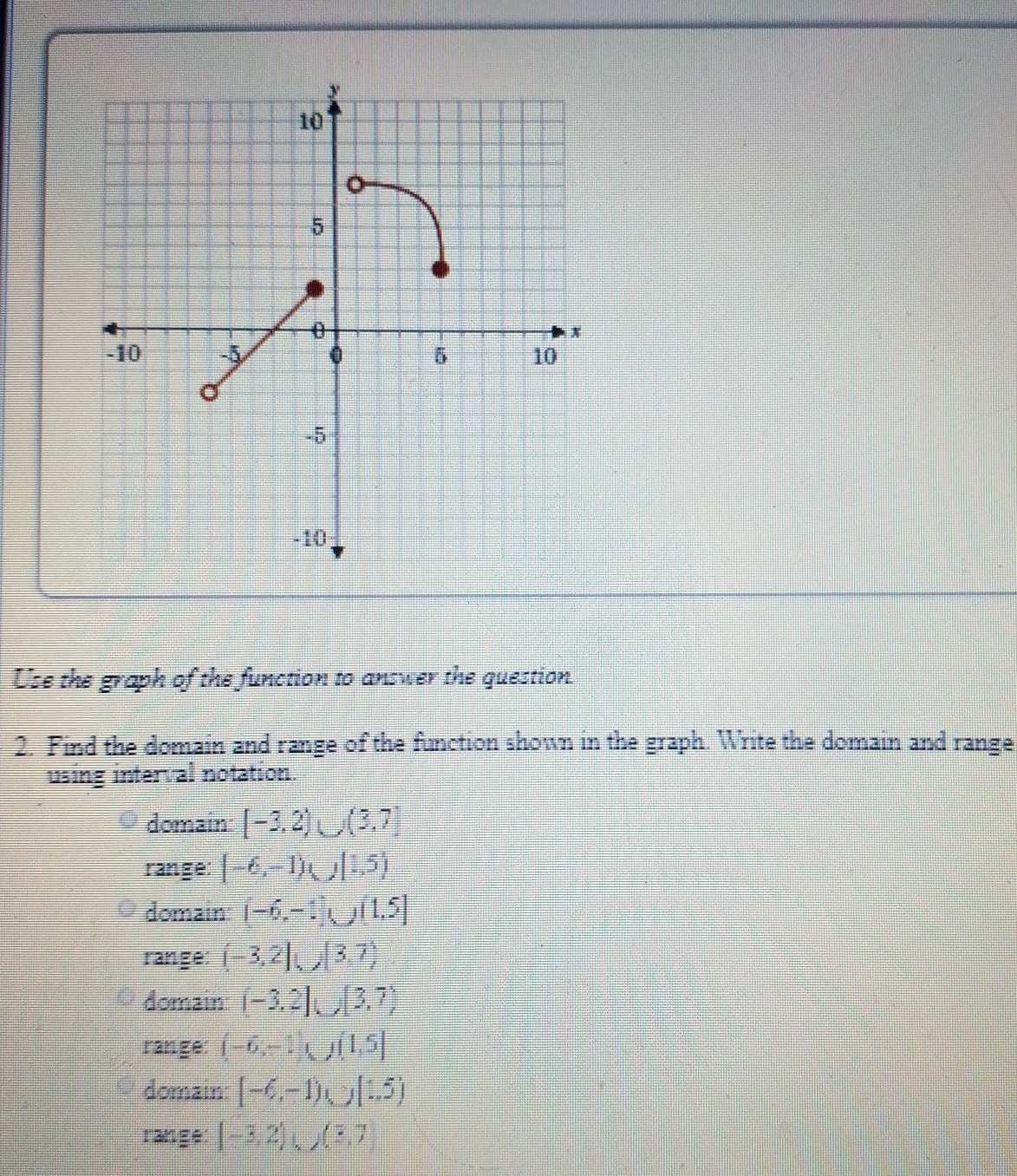
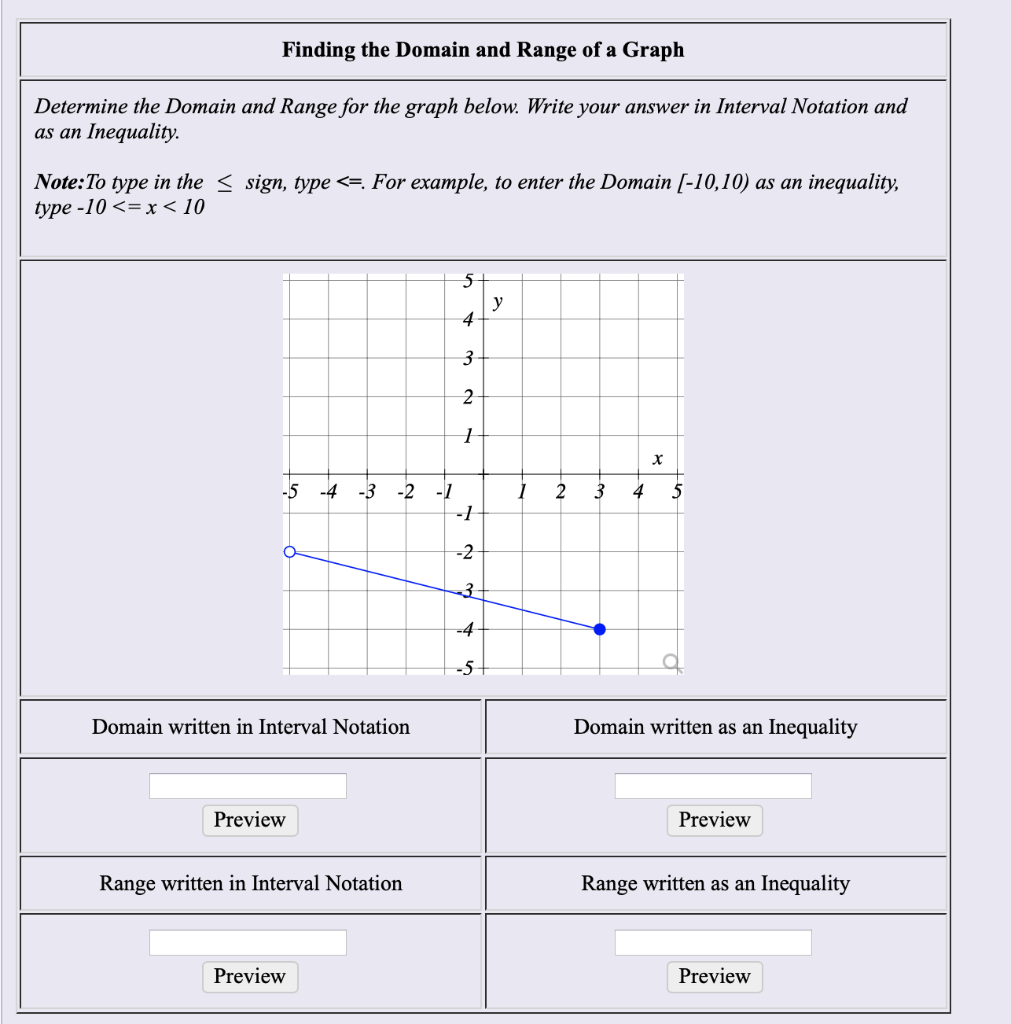
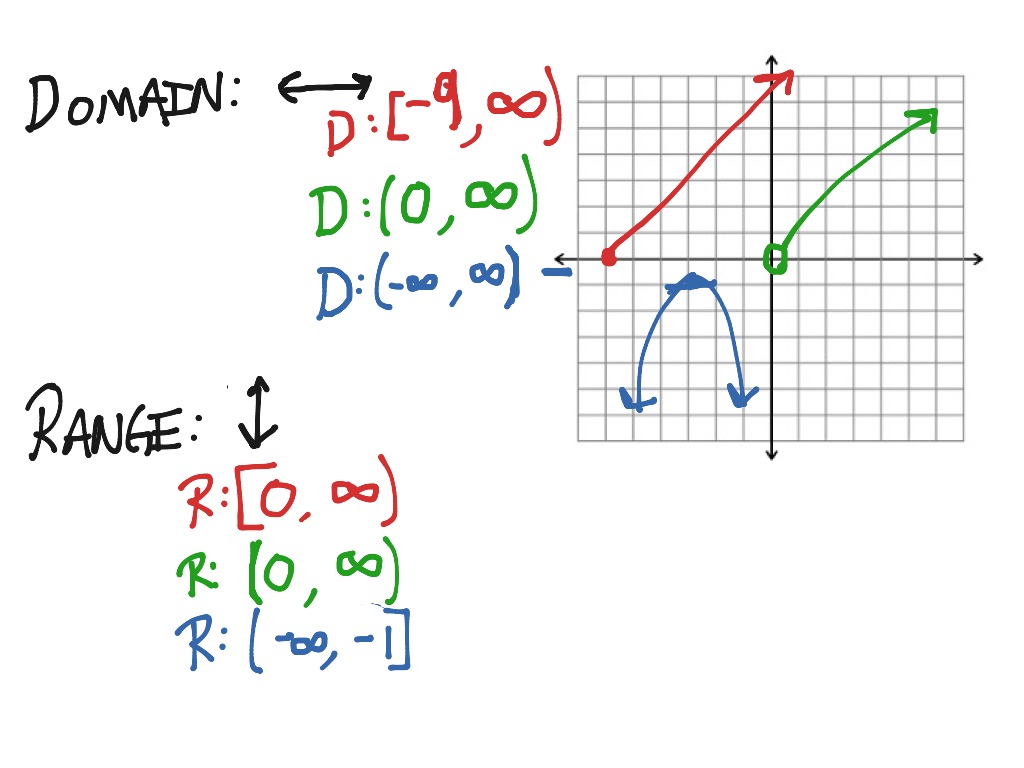
How To Write Domain In Interval Notation – How To Write Domain In Interval Notation
| Pleasant in order to the website, on this moment I will demonstrate in relation to How To Factory Reset Dell Laptop. And after this, this is actually the first image:

Why not consider impression previously mentioned? is in which awesome???. if you think maybe and so, I’l l provide you with a few picture again below:
So, if you wish to have all of these outstanding photos regarding (How To Write Domain In Interval Notation), just click save link to download these images in your personal pc. They are all set for download, if you love and wish to have it, just click save logo on the article, and it’ll be immediately saved in your home computer.} As a final point if you wish to find new and the recent picture related to (How To Write Domain In Interval Notation), please follow us on google plus or book mark the site, we attempt our best to present you daily up-date with fresh and new pictures. Hope you love staying here. For some updates and latest information about (How To Write Domain In Interval Notation) images, please kindly follow us on twitter, path, Instagram and google plus, or you mark this page on book mark section, We try to offer you up-date periodically with all new and fresh photos, love your surfing, and find the right for you.
Thanks for visiting our site, contentabove (How To Write Domain In Interval Notation) published . At this time we are delighted to declare that we have found an awfullyinteresting topicto be reviewed, namely (How To Write Domain In Interval Notation) Lots of people searching for info about(How To Write Domain In Interval Notation) and certainly one of these is you, is not it?