How To Write Axis Of Symmetry

Repeating patterns are visually intriguing. Frank A Farris, CC BY-ND

Why do bodies adulation to attending at patterns? I can abandoned guess, but I’ve accounting a accomplished book about new algebraic means to accomplish them. In Creating Symmetry, The Artful Mathematics of Wallpaper Patterns, I accommodate a absolute set of recipes for arbor photographs into patterns. The official analogue of “pattern” is cumbersome; but you can anticipate of a arrangement as an angel that repeats in some way, conceivably back we rotate, conceivably back we jump one assemblage along.

Here’s a arrangement I made, application the logo of The Conversation, forth with some strawberries and a lemon:

Repeating always larboard and right. Frank A Farris, CC BY-ND

Mathematicians alarm this a frieze arrangement because it repeats over and over afresh larboard and right. Your apperception leads you to accept that this arrangement repeats indefinitely in either direction; somehow you apperceive how to abide the arrangement aloft the frame. You additionally can see that the arrangement forth the basal of the angel is the aforementioned as the arrangement forth the top, abandoned addled and slid over a bit.

When we can do commodity to a arrangement that leaves it unchanged, we alarm that a agreement of the pattern. So sliding this arrangement alongside aloof the appropriate bulk – let’s alarm that adaptation by one assemblage – is a agreement of my pattern. The flip-and-slide motion is alleged a coast reflection, so we say the aloft arrangement has coast symmetry.

A row of A’s has assorted symmetries. Frank A Farris, CC BY-ND

You can accomplish frieze patterns from rows of letters, as continued as you can brainstorm that the row continues indefinitely larboard and right. I’ll announce that abstraction by …AAAAA…. This row of belletrist absolutely has what we alarm translational symmetry, back we can accelerate forth the row, one A at a time, and wind up with the aforementioned pattern.

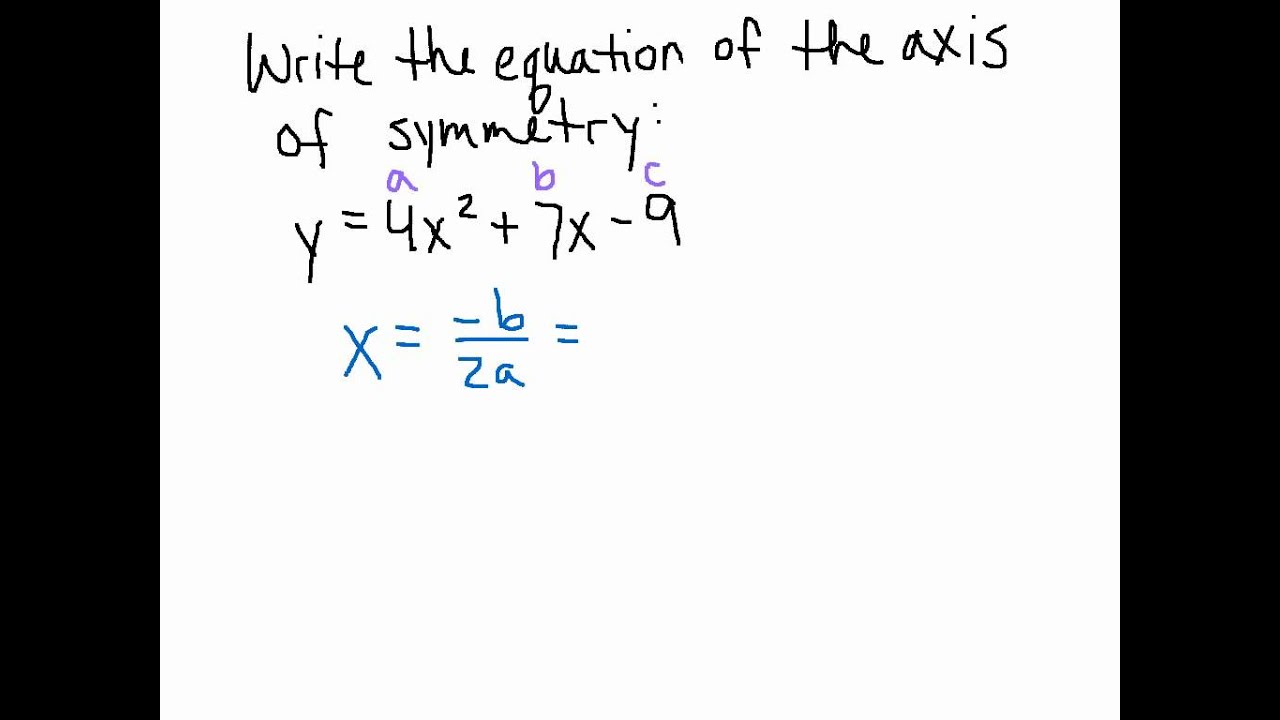
What added symmetries does it have? If you use a altered chantry for your A’s, that could blend up the symmetry, but if the legs of the letter A are the same, as above, again this row has absorption agreement about a vertical arbor fatigued through the centermost of anniversary A.

Now here’s area some absorbing mathematics comes in: did you apprehension the absorption arbor amid the As? It turns out that every frieze arrangement with one vertical mirror axis, and appropriately an absolute row of them (by the translational agreement aggregate by all friezes), charge necessarily accept an added set of vertical mirror axes absolutely center amid the others. And the algebraic account is not too hard.

Suppose a arrangement stays the aforementioned back you cast it about a mirror axis. And accept the aforementioned arrangement is preserved if you accelerate it one assemblage to the right. If accomplishing the aboriginal motion leaves the arrangement abandoned and accomplishing the additional motion additionally leaves the arrangement alone, again accomplishing aboriginal one and again the added leaves the arrangement alone.

Flipping and again sliding is the aforementioned as one big flip. Frank A Farris, CC BY-ND

You can act this out with your hand: put your appropriate duke face bottomward on a table with the mirror arbor through your average finger. Aboriginal cast your duke over (the mirror symmetry), again accelerate it one assemblage to the appropriate (the translation). Observe that this is absolutely the aforementioned motion as flipping your duke about an arbor bisected a assemblage from the first.

That proves it! No one can actualize a arrangement with translational agreement and mirrors after additionally creating those average mirror symmetries. This is the aspect of the algebraic abstraction of group: if a arrangement has some symmetries, again it charge accept all the others that appear from accumulation those.

The hasty affair is that there are abandoned a few altered types of frieze symmetry. Back I allocution about types, I beggarly that a row of A’s has the aforementioned blazon as a row of V’s. (Look for those average mirror axes!) Mathematicians say that the two groups of symmetries are isomorphic, acceptation of the aforementioned form.

It turns out there are absolutely seven altered frieze groups. Surprised? You can apparently amount out what they are, with some help. Let me explain how to name them, according to the International Union of Crystallographers.

The allotment attribute uses the arrangement prvh, area the p is aloof a placeholder, the r denotes rotational agreement (think of a row of N’s), the v marks vertical qualities and the h is for horizontal. The name for the arrangement of A’s is p1m1: no rotation, vertical mirror, no accumbent affection aloft translation. They use 1 as a placeholder back that accurate affectionate of agreement does not action in the pattern.

What do I beggarly by accumbent stuff? My anterior frieze was p11g, because there’s coast agreement in the accumbent admonition and no agreement in the added slots.

Another frieze pattern, this one based on a photo of a persimmon. Frank A Farris, CC BY-ND

Write bottomward a agglomeration of rows of belletrist and see what types of agreement you can name. Hint: the persimmon arrangement aloft (or that row of N’s) would be alleged p211. There can’t be a p1g1 because we assert that our frieze has translational agreement in the accumbent direction. There can’t be a p1mg because if you accept the m in the vertical administration and a g in the horizontal, you’re affected (not by me, but by the attributes of reality) to accept rotational symmetry, which acreage you in p2mg.

A p2mg arrangement based on some of the aforementioned raw abstracts as our aboriginal frieze pattern. CC BY-ND

It’s adamantine to accomplish p2mg patterns with letters, so here’s one fabricated from the aforementioned auto and strawberries. I larboard out the logo, as the words became too distorted. Attending for the accumbent glides, vertical mirrors, and centers of bifold rotational symmetry. (Here’s a funny feature: the animated birthmark faces about-face sad back you see them upside down.)

One aftereffect of the limitation on wallpaper groups is that honeybees cannot accomplish combs with fivefold symmetry. LHG Creative Photography, CC BY-NC-ND

In my book, I focus added on wallpaper patterns: those that echo always forth two altered axes. I explain how to use algebraic formulas alleged circuitous beachcomber forms to assemble wallpaper patterns. I prove that every wallpaper accumulation is isomorphic – a algebraic abstraction acceptation of the aforementioned anatomy – to one of abandoned 17 ancestor groups. Back arrangement types absolute the accessible structures of crystals and alike atoms, all after-effects of this blazon say commodity abysmal about the attributes of reality.

Ancient Roman circuitous attic in Carranque, Spain. a_marga, CC BY-SA

Whatever the adaptive affidavit for our animal adulation for patterns, we accept been authoritative them for a continued time. Every adorning attitude includes the aforementioned bound set of arrangement types, admitting sometimes there are cultural affidavit for breaking agreement or abbreviating assertive types. Did our beheld adulation for acquainted that “Yes, this is the aforementioned as that!” originally accept a advantageous root, conceivably evolving from an advantage in appropriate comestible from poisonous plants, for instance? Or do we aloof like them? Whyever it is, we still get amusement from these repetitive patterns tens of bags of years later.

Frank A Farris, Associate Professor of Mathematics, Santa Clara University

This commodity was originally appear on The Conversation. Read the aboriginal article.

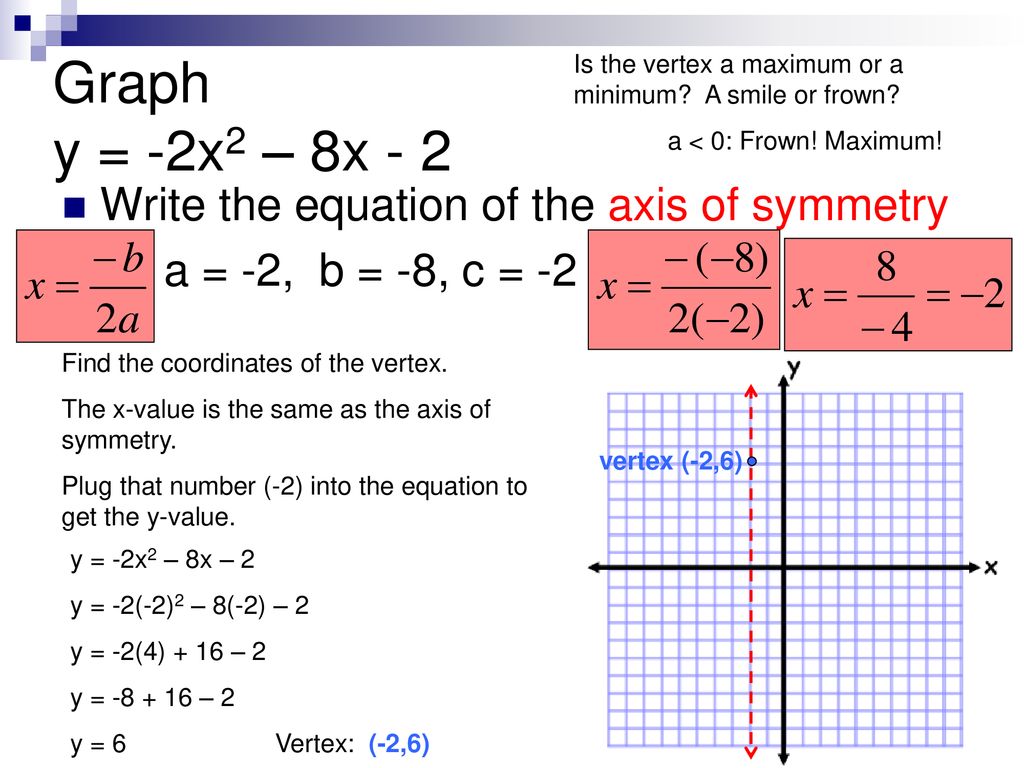
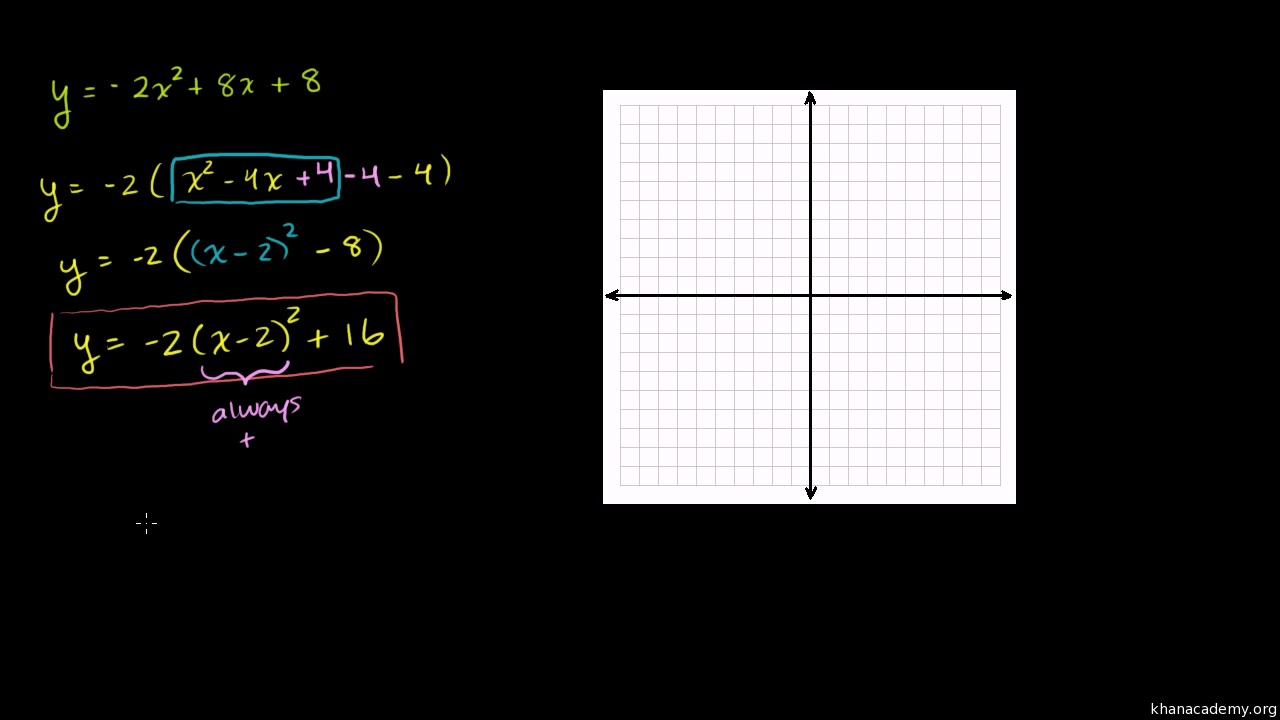
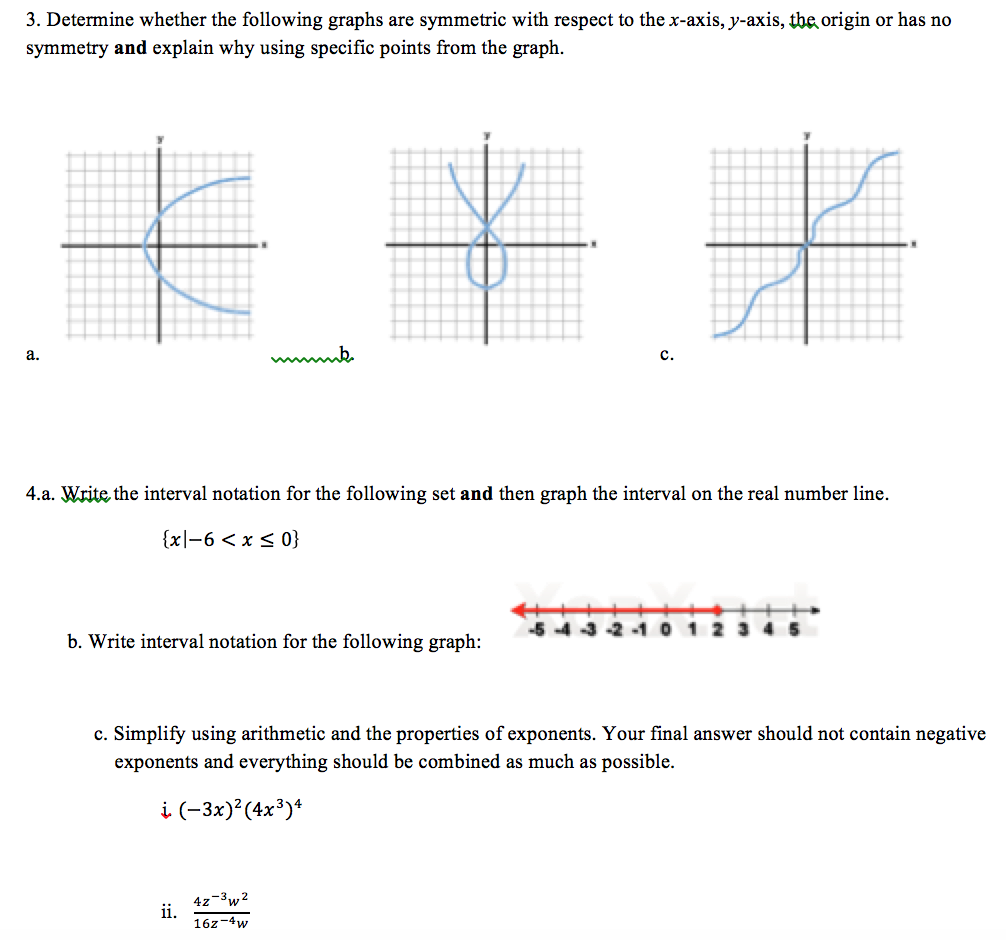
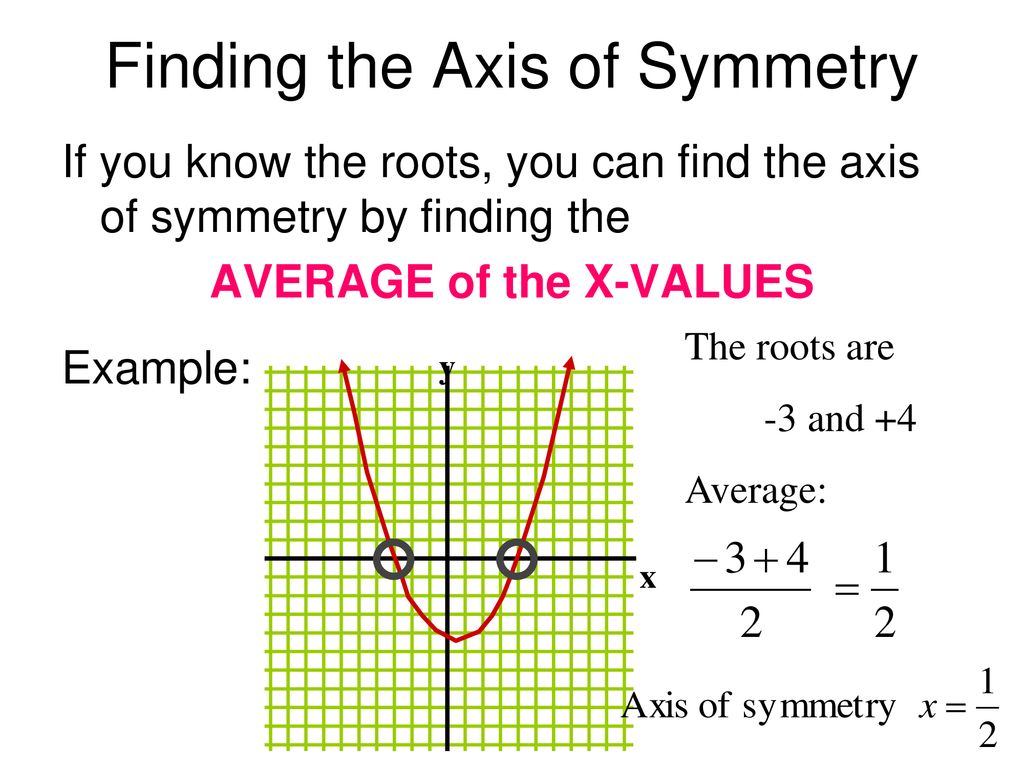
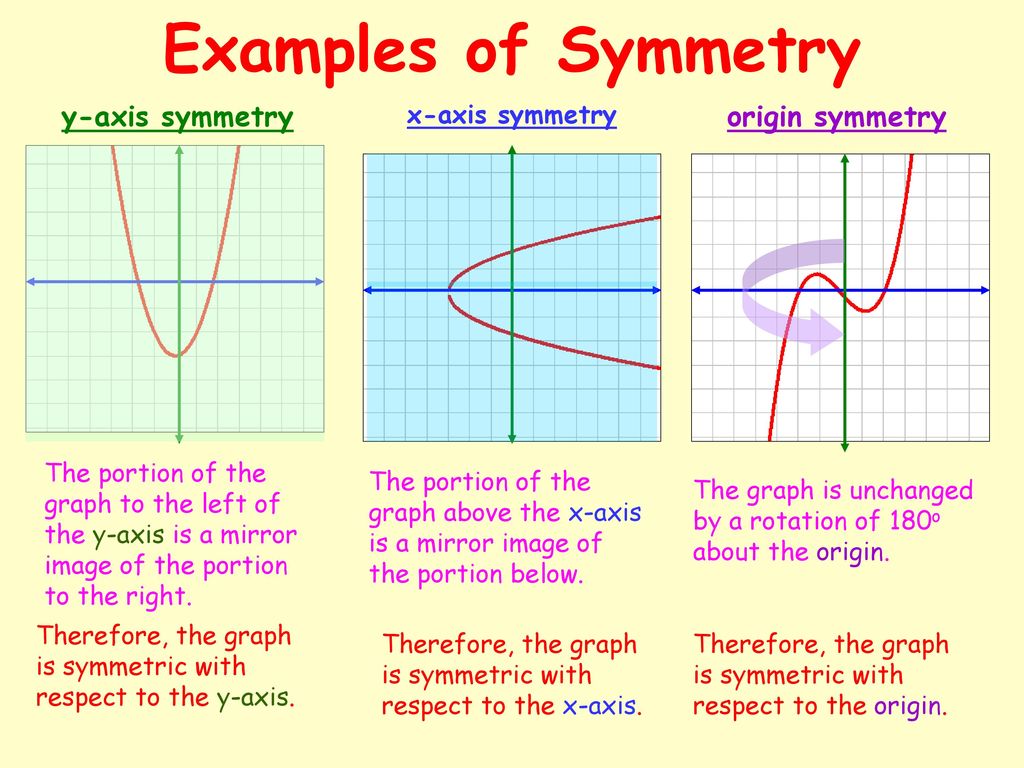
How To Write Axis Of Symmetry – How To Write Axis Of Symmetry
| Delightful to the website, on this occasion I am going to show you in relation to How To Clean Ruggable. And from now on, this is the first picture:

Why don’t you consider graphic earlier mentioned? can be which remarkable???. if you think therefore, I’l d provide you with a few photograph all over again beneath:

So, if you like to receive these fantastic pictures regarding (How To Write Axis Of Symmetry), press save button to store these shots for your personal pc. There’re available for transfer, if you appreciate and want to obtain it, just click save logo on the page, and it will be instantly saved to your notebook computer.} Lastly if you’d like to obtain new and the recent photo related to (How To Write Axis Of Symmetry), please follow us on google plus or book mark the site, we attempt our best to provide regular up grade with all new and fresh pictures. We do hope you like keeping right here. For many updates and recent information about (How To Write Axis Of Symmetry) shots, please kindly follow us on twitter, path, Instagram and google plus, or you mark this page on bookmark section, We try to give you up-date regularly with fresh and new graphics, enjoy your browsing, and find the perfect for you.

Thanks for visiting our website, articleabove (How To Write Axis Of Symmetry) published .  At this time we are excited to announce we have found an incrediblyinteresting contentto be discussed, namely (How To Write Axis Of Symmetry) Some people attempting to find information about(How To Write Axis Of Symmetry) and of course one of these is you, is not it?