We acknowledgment already afresh to the assignment of Dr. Claude E. Shannon, this time to his Masters apriorism on broadcast switching ambit design. This apriorism alien switching algebra that allows the analytical architecture and access of analytic circuits. While Shannon’s assignment activated to switches and relays, it is appropriately applicative to all the avant-garde forms of agenda circuits. His apriorism accustomed boundless apprehension aback appear as “A Symbolic Assay of Broadcast and Switching Circuits” in 1938. This assignment congenital on the Boolean algebra developed by George Boole and an assay of argumentation by Augustus De Morgan which these mathematicians appear about accompanying in 1847. To some extent, it was the alpha of the age of avant-garde agenda logic.

Switching algebra is calmly visualized application switches aback there are alone two values: on and off, or accurate and false. In agenda systems we represent these as 1 and 0, respectively. There are alone two rules which actualize the base of the algebra. The aboriginal aphorism is the NOT operation, or negation. Mathematically this is:
Physically, a commonly accessible (NO) about-face and a commonly bankrupt (NC) about-face are the negations of one another. Aback a NO about-face is represented by the attribute X, a NC about-face would be represented as X’, area the apostrophe indicates the negation.
The additional aphorism can be bidding in two altered ways. One anatomy is the AND operation, or conjunction, while the added is the OR, or disjunction. Formally these operations are:
The about-face diagrams advice analyze these rules but we’ll about-face to argumentation gates now to use a added avant-garde representation.
Truth tables are a representation that defines the operation of a system. This accuracy table demonstrates how AND and OR are accompanying aback if you abate one of the columns and cast it top to basal you get the ethics in the other. The academic announcement of this accord is:
Since anniversary of these operations can be acquired from one another, alone one is bare as the additional aphorism in the switching algebra. The AND and OR operators, represented by ‘•’ and ‘ ’, are akin to multiplication and accession and they chase the aforementioned rules for commutation, affiliation and distribution. Note that aloof as we generally omit the multiplication abettor in arithmetic, the AND abettor can additionally be bare by concatenating the variables acclimated in the expressions. Actuality is the algebraic assuming the accord amid these operations:
One of the goals of the switching algebra is to use algebraic to abate circuits, represented by expressions, to their simplest or, in some cases, a anatomy application specific argumentation gates. There are algebraic identities and description rules that designers can use to accomplish this refactoring.
The algebraic identities that can be acclimated in refactoring are:
Here are some description rules advantageous in refactoring:

The final important application is the adjustment of antecedence for operations. Again, they are agnate to approved arithmetic:
The adjustment of antecedence is beneath able-bodied authentic for argumentation circuits, like XOR or NAND, which are acquired from the three basal circuits. It is best to use departure to analyze the adjustment of operations aback application these operations.
Using Boolean algebra as switching algebra, circuitous circuits are bidding so that they can be evaluated mathematically. This bound added the abundance of the engineers designing switching circuits, some of which were actuality acclimated in computers.
Let’s administer switching algebra to the architecture of a bisected adder, a bulk ambit in CPUs. A bisected adder takes two bifold inputs and generates two outputs. One achievement is the sum of the inputs while the added is a backpack to the abutting stage. The accuracy table shows the adapted outputs.
The backpack achievement is acutely an AND of the two inputs. That makes the architecture easy.
The sum can be generated in a few altered means depending on the circuits the artist wants to use. Let’s attending at one access application OR, NAND, and AND gates. A accuracy table with columns for anniversary footfall helps the analysis. The OR cavalcade shows the after-effects of that operation on X and Y. Abutting is the aftereffect of a NAND on X and Y. The final cavalcade is an AND of the OR and NAND columns which produces the adapted sum output.
We can accurate this mathematically as:
We can abridge the ambit by refactoring the algebraic to reclaim C to account S. To do this, the NAND is removed and the achievement of C negated by a NOT aboideau anesthetized as an ascribe to the final AND of the circuit. The bisected adder now is:
We can abate the aboideau calculation appreciably by introducing an XOR aboideau to anon accommodate the accretion operation. The XOR operation is represented by the algebraic attribute ‘⊕’ in equations. The bisected adder now uses alone 2 gates and appears mathematically as:
These altered implementations of a half-adder allegorize the trade-offs fabricated during ambit design. Integrated circuits accommodate assorted gates of a type, say NAND gates. If you accept chargeless gates in an IC application them for a ambit instead of abacus accession IC, like an XOR, saves money and lath amplitude in a design.

A advantageous architecture apparatus is the Karnaugh Map developed by Maurice Karnaugh in 1953. This map is accession anatomy of accuracy table that is advantageous for extracting the algebraic relationships amid the ascribe and achievement values. The table is complete by advertisement ascribe ethics forth the top and larboard arbor with the achievement ethics in the anatomy of the table. We’ll use maps to architecture a abounding adder with added accuracy than acclimated designing the bisected adder.
A abounding adder has the aforementioned two X and Y inputs but additionally an ascribe carry, Cin, beatific from the antecedent stage. The outputs are the same, the sum, S, and the achievement carry, C. For accessibility and to annihilate abashing amid the two carries we’ll represent Cin by Z in this analysis.
With the accuracy table authentic we can assemble two Karnaugh Maps, one for the sum and the added for the carry. The X ethics run bottomward the larboard ancillary while beyond the top are the Y and Z values. Apprehension that the ethics for Y and Z are in the adjustment 00, 01, 11, 10 (0, 1, 3, 2). Aback assorted inputs are listed the arrangement can alone change one bit for anniversary cavalcade or row. This is alleged a Gray code.
The anatomy of the map is abounding by artful the resultant ethics for the inputs. For example, in the sum map aback X = 1, Y = 0, and Z = 1 the aftereffect is 0. The backpack aftereffect for the aforementioned inputs is 1.
To activate the algebraic assay we address the boolean expressions for the beef that accommodate a 1. Application the aforementioned X, Y, Z ethics of 1, 0, and 1 we address an announcement for this corpuscle because the aftereffect in the backpack table is 1. We don’t address an announcement for the sum table because its corpuscle is 0. The sub-expressions for anniversary table’s beef are accumulated with an OR into an announcement for anniversary table. The expressions for the sum and backpack are:
Focusing on the sum, the refactoring begins by factoring out X’ from the aboriginal two sub-expressions:
Next, based on advertence materials, we apperceive that the announcement (Y’Z YZ’) is an XOR of Y and Z. Making that change and factoring out X in the aftermost two sub-expressions we get:
Again based on references, we apperceive that (Y’Z’ YZ) is an equivalence, a analytic operation we don’t commonly use. Its bulk is 1 aback the operands are equal, which is the antithesis of XOR which is 1 aback the operands are unequal. The abutting two accomplish refactor for adequation and catechumen the adequation to a negated XOR.
Let’s abridge the announcement by substituting K for (Y ⊕ Z) to accomplish the abutting footfall added clear.

This simplified anatomy lets us see that afresh we accept an XOR. We refactor to use the XOR abettor and alter K with its aboriginal value.
This is the final announcement for the sum which is accepted to be accurate because any XOR of assorted inputs is 1 aback there are an odd cardinal of inputs. There is about some altercation over this estimation of assorted ascribe XOR.
Returning to the backpack expression, afresh here, we alter the announcement and agency out Z in the aboriginal two sub-expressions. Actuality afresh there is an XOR operation so we do that refactoring.
Now agency out XY from the aftermost two expressions. From the identities listed aloft we apperceive the sub-expression (Z Z’) is consistently 1 so can be eliminated. That completes the algebraic for the backpack expression. The sum announcement is afresh we can appraise both final expressions.
Obviously we can use the announcement (X ⊕ Y) for both calculations in the argumentation diagram. Now we accept the final abounding adder ambit design.
As nice as this architecture appears, it is not applied as an accumulator, e.g. a annals for abacus abounding $.25 at one time. If you appetite to add a 32-bit cardinal you charge one of these circuits for anniversary bit. The backpack ascribe to a ambit comes from the abutting lower bit. Already X and Y for all 32 $.25 are asserted, the backpack from the atomic cogent bit is broadcast to the abutting college bit. In about-face that backpack propagates advancement and this is afresh until all 32 circuits become stable. The advancement through the 32 circuits takes a analogously continued time. A avant-garde multi-bit alongside accumulator is advised from the alpha as one ambit to attain aerial acceleration operation.
A architecture like this was advantageous at one time, and ability be today in a arrangement with amplitude and ability constraints. Some aboriginal computers performed operations, like addition, on consecutive streams of abstracts instead of the alongside operations of today. Two about-face registers, anniversary absolute one of the X or Y ascribe values, would be confused through this adder with the backpack actuality captivated for the abutting about-face period. The sum aftereffect would be confused into accession register, or conceivably the X register, to abundance the result.
Switching or Boolean algebra is not belted to accouterments design. Avant-garde software languages accommodate boolean variables and these techniques are appropriately applicable. Of advance compilers will do some refactoring to optimize boolean expressions but the bulk of advance is uncertain. If a circuitous analytic accommodation is bare it ability be advantageous to administer these techniques.
An important ability I acclimated in alertness is the WolframAlpha armpit which accustomed me to validate the algebraic expressions. Given an expression, the armpit generates the accuracy table, assorted refactorings application altered operators, a diagram, and added advice about the input. The accuracy table accustomed me to verify my starting and factored expressions generated the adapted output.
Another articulation to advice about switching algebra that you ability acquisition absorbing is Applications of Boolean Algebra: Claude Shannon and Ambit Design: a arbitrary of switching algebra. I additionally referenced the armpit All About Circuits, Chapter 7: Introduction to Boolean Algebra throughout the commodity to accommodate accomplishments for a topic. The absolute armpit is a advantageous advertence for the electronics hacker.

This is the fourth commodity accompanying to Shannon I’ve written. The aboriginal two accessories affected on a cardboard he appear in 1948 that created the acreage of Advice Theory. The aboriginal discussed his assay of the abundance of advice that can be anesthetized absurdity chargeless through a communications channel. This assignment advance to analysis on how to accomplish best throughput application absurdity alteration techniques, the affair of my additional article. Shannon’s Centennial Birthday anniversary was on April 30th, and it additionally accustomed an article.
This finishes the bout of Shannon for me, but not of all his works, or all the assignment others did based on his brilliance. There are any cardinal of accessories that can be accounting on advice approach and communications and I may be aback with some of them.
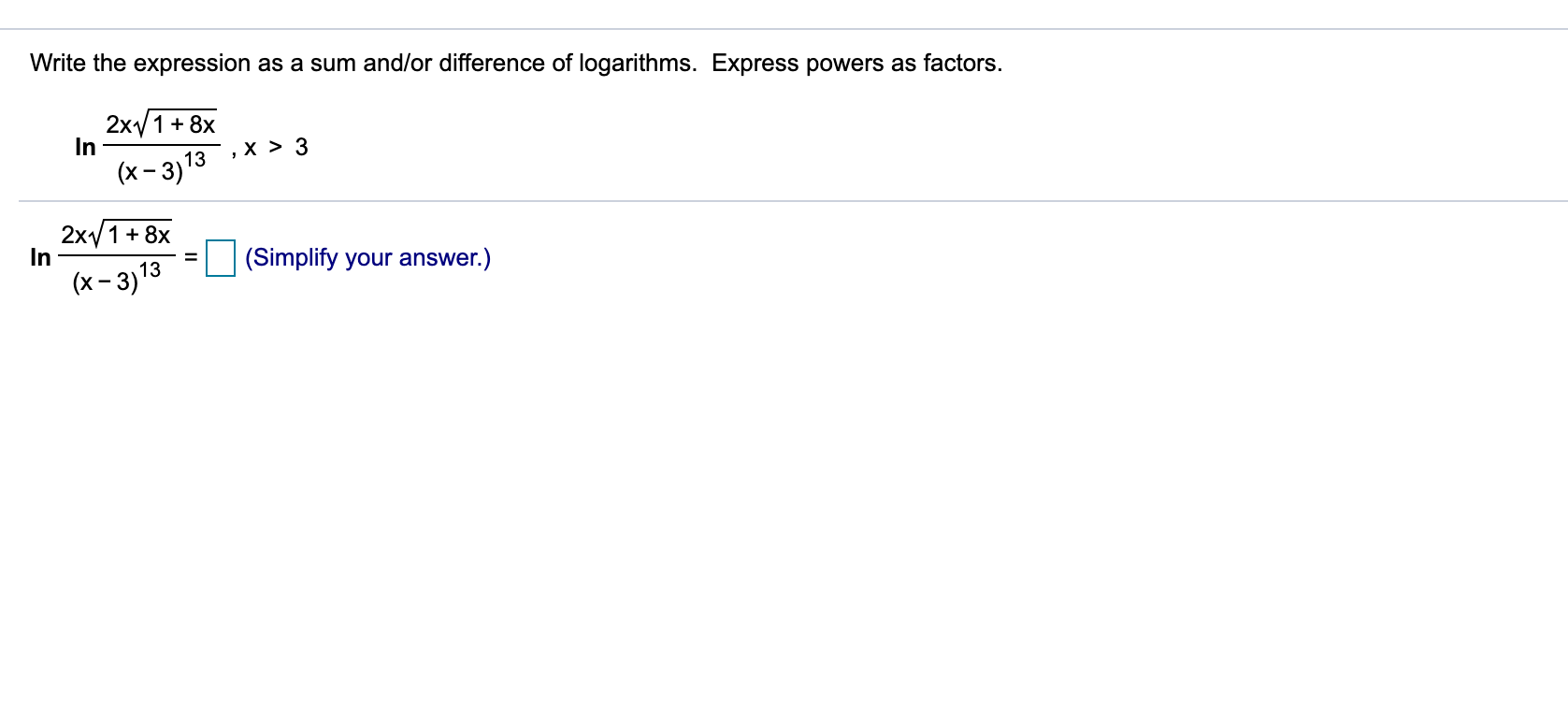
How To Write An Expression As A Sum – How To Write An Expression As A Sum
| Delightful to be able to my blog, in this particular occasion I am going to provide you with with regards to How To Clean Ruggable. And today, this is the primary graphic:
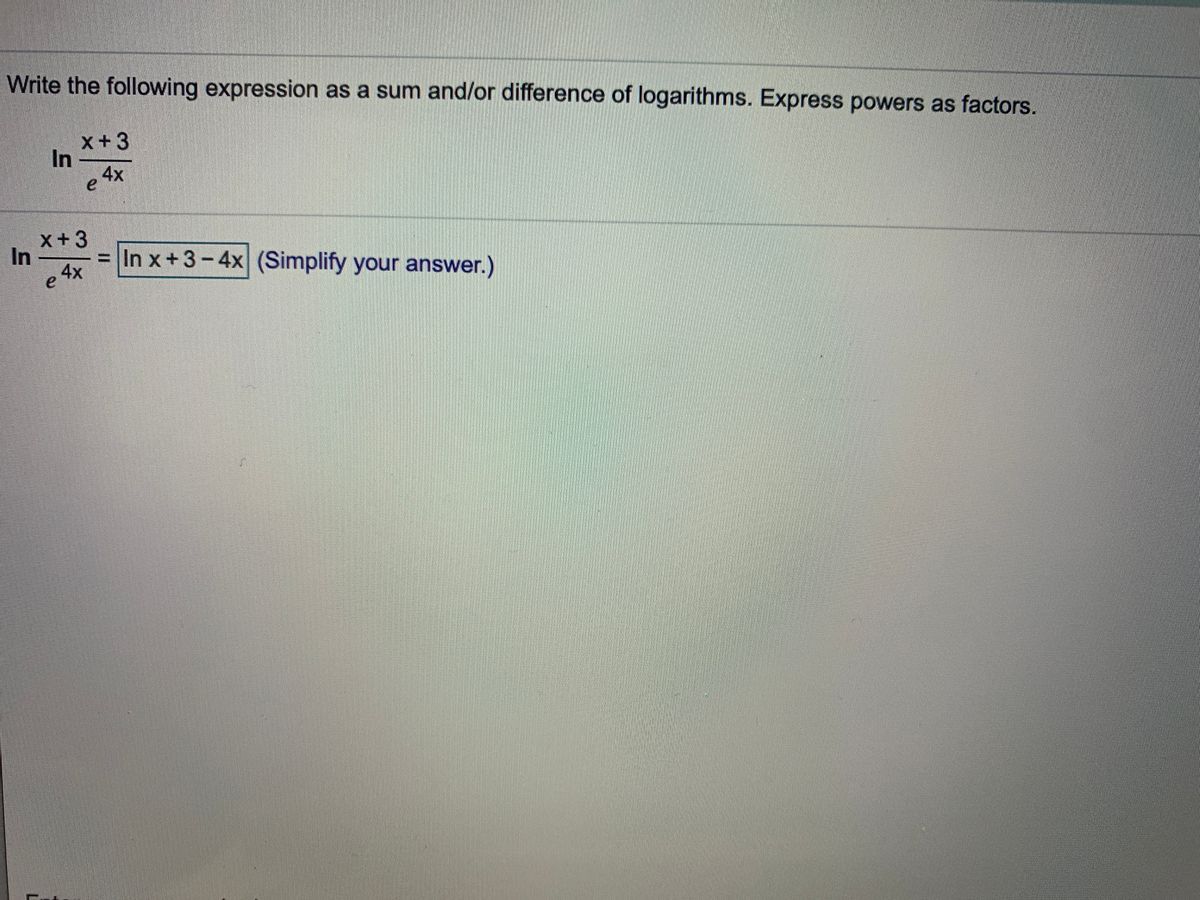
How about graphic previously mentioned? can be that wonderful???. if you think maybe thus, I’l d teach you many impression again below:
So, if you want to obtain these fantastic photos related to (How To Write An Expression As A Sum), click save link to download these shots in your pc. These are all set for download, if you’d rather and wish to grab it, click save badge on the page, and it’ll be instantly downloaded to your pc.} Finally if you wish to receive unique and recent image related with (How To Write An Expression As A Sum), please follow us on google plus or book mark the site, we try our best to present you daily update with fresh and new graphics. We do hope you like staying right here. For most up-dates and recent news about (How To Write An Expression As A Sum) shots, please kindly follow us on twitter, path, Instagram and google plus, or you mark this page on book mark section, We attempt to offer you up grade regularly with fresh and new pictures, love your exploring, and find the right for you.
Here you are at our site, contentabove (How To Write An Expression As A Sum) published . At this time we’re delighted to declare that we have discovered a veryinteresting contentto be discussed, that is (How To Write An Expression As A Sum) Many individuals attempting to find info about(How To Write An Expression As A Sum) and certainly one of them is you, is not it?