Recall that the band-aid of the initial-value botheration (y^prime=kytext{,}) (y(0)=Atext{,}) is accustomed by (ds y=Ae^{kx}text{.})
Solve the afterward problems.
An bulk of (A_0) CAD is invested adjoin annual absorption of (p%text{.}) Give the announcement for (A(t)text{,}) the bulk of the advance in CAD afterwards (t) years if the absorption is circuitous continuously by autograph bottomward the cogwheel blueprint that (A) satisfies and analytic it.
Jane invests 10,000 CAD adjoin a annual absorption (p%text{,}) circuitous continuously. Afterwards 4 years the bulk of her advance is 15,000 CAD. What is (ptext{?})
The bulk at which a apprentice learns new actual is proportional to the aberration amid a maximum, (Mtext{,}) and the bulk she already knows at time (ttext{,}) (A(t)text{.}) This is alleged a acquirements curve.
Write a cogwheel blueprint to archetypal the acquirements ambit described.
Solve the cogwheel blueprint you created in allotment (a).
If took a apprentice 100 hours to apprentice (50%) of the actual in Math 151 and she would like to apperceive (75%) in adjustment to get a (Btext{,}) how abundant best she should study? You may accept that the apprentice began alive none of the actual and that the best she ability accomplish is (100%text{.})
The absorption of booze (in (%)) in the blood, (C(t)text{,}) obeys the adulteration cogwheel equation:
begin{equation*} frac{dC}{dt}=-frac{1}{k}Ctext{,} end{equation*}
where (k=2.5) hours is alleged the abolishment time. It is estimated that a macho belief 70 kg who drinks 3 pints of beer over a aeon of one hour has a absorption of (1%) of booze in his blood. The accustomed acknowledged absorption for active is a best of (0.5%text{.})
If a being has a claret booze absorption of (1%text{,}) how continued should she/he delay afore active in adjustment not to balk the law. You may charge the bulk (ln 2approx 0.7text{.})
What is the antecedent ((t=0)) bulk of change in the concentration?

Note: The permissible BAC absolute in the Bent Code of Canada is .08 (80 milligrams of booze in 100 millilitres of blood). Some apostle a lower bent absolute of .05 (50 milligrams of booze in 100 millilitres of blood).
The absorption of booze (in (%)) in the blood, obeys the adulteration blueprint (displaystyle frac{dC}{dt}=-0.4Ctext{.}) If a being has a claret booze absorption of (2%text{,}) how continued would it booty for claret booze absorption to bead to (1%text{?}) Booty that the abolishment time is accustomed in hours.
Carbon dating is acclimated to appraisal the age of an age-old animal skull. Let (f(t)) be the admeasurement of aboriginal (^{14}C) atoms actual in the scull afterwards (t) years of radioactive decay. Since (^{14}C) has a bisected activity of 5700 years we accept (f(0)=1) and (f(5700)=0.5text{.})
Sketch the blueprint of (f(t)) against (t) in the area (0leq tleq 20000text{.}) Characterization at atomic two credibility of your artifice and be abiding to characterization the axes.
Write an announcement for (f(t)) in agreement of (t) and added afterwards constants such as (ln 2text{,}) (sin 5text{,}) (e^3text{,}) and (1/5700text{.}) (Note: Not all of these constants charge arise in your answer!)
Suppose that alone (15%) of the aboriginal (^{14}C) is begin to abide in the skull. Derive from your antecedent answer, an announcement for the estimated age of the skull.
The accumulation of a sample of a radioactive atom decays according to the aphorism (displaystyle frac{dm}{dt}=-5mtext{.}) Determine the half-life of this particle.
Plutonium-239 is allotment of the awful radioactive decay that nuclear ability affairs produce. The half-life of plutonium-239 is 24,110 years. Suppose that 10 kg of plutonium-239 has leaked into and attenuated a lake. Let (m(t)) denote the accumulation of plutonium-239 that charcoal in the basin afterwards (t) years.
Find an announcement for (m(t)) based on the advice given.
How abundant accumulation charcoal in the basin afterwards 1000 years.
Suppose the basin is advised safe for use afterwards alone 1 kg of the plutonium-239 remains. How abounding years will this take?
On a assertive day, a scientist had 1 kg of a radioactive actuality (X) at 1:00 pm. Afterwards six hours, alone 27 g of the actuality remained. How abundant actuality (X) was there at 3:00 pm that aforementioned day?

In a assertive ability of bacteria, the cardinal of bacilli added tenfold in 10 hours. Bold accustomed growth, how continued did it booty for their cardinal to double?
A bacterial ability starts with 500 bacilli and afterwards three hours there are 8000. Accept that the ability grows at a bulk proportional to its size.
Find an announcement in (t) for the cardinal of bacilli afterwards (t) hours.
Find the cardinal of bacilli afterwards six hours.
Find an announcement of the anatomy (ds mfrac{ln a}{ln b}) with (mtext{,}) (atext{,}) and (b) absolute integers for the cardinal of hours it takes the cardinal of bacilli to ability a million.
A bacilli ability starts with 500 bacilli and grows at a bulk proportional to its size. Afterwards three hours there are 8000 bacteria. Acquisition the cardinal of bacilli afterwards four hours.
The bacilli citizenry (P(t)) quadruples every 15 minutes. The antecedent bacilli citizenry is (P(0)=10text{.}) You ability charge the afterward values: (ln 6approx 1.6text{,}) (ln 8approx 2.08text{,}) ((ln 10)/(ln 2)approx 3.32text{,}) (ln 2approx 0.69text{,}) (4^3=64text{,}) (4^6=4096text{,}) (4^9=262144text{,}) (4^{12}=16777216text{.})
What is the citizenry afterwards three hours?
How abundant time does it booty for the citizenry to abound to 1 billion?
The citizenry of a bacilli ability grows at a bulk that is proportional to the admeasurement of the population.
Let (P) denote the citizenry of the ability at time (ttext{.}) Express (dP/dt) in agreement of the proportional connected (k) and (Ptext{.})
If the citizenry is 240 at time (t=1) and is 360 at time (t=2text{,}) acquisition a blueprint for the cardinal of bacilli at time (ttext{.}) ((t) in hours.)

How abounding bacilli were there at time (t=0text{.}) Your acknowledgment should be a absolute integer.
What is the bulk of (dP/dt) back (t=0text{.})
Assume that Math 151 in abatement of 2000 had an enrolment of 500 acceptance and in abatement 2002 had an enrolment of 750 students. Accept additionally that if (P(t)) is the enrolment at time (t) (let (t) be in years, with (t=0) agnate to year 2000), again (P'(t)=kP(t)) for some connected (ktext{.}) Calculate (P(500)) (the enrolment in Math 151 in abatement of 2500). Simplify your acknowledgment as abundant as possible. The acknowledgment will be absolutely large.
A afresh brewed cup of coffee has temperature (95^circ)C and is in a (20^circ)C room. Back its temperature is (70^circ)C, it is cooling at the bulk of (1^circ)C per minute. Back does this occur?
A cup of coffee, cooling off in a allowance at temperature (20^0)C, has cooling connected (k=0.09)min(^{-1}text{.})
How fast is the coffee cooling (in degrees per minute) back its temperature is (T=80^circ)C?
Use beeline approximation to appraisal the change in temperature over the abutting 6 abnormal back (T=80^circ)C.
The coffee is served at a temperature of (90^circtext{.}) How continued should you delay afore bubbler it if the optimal temperature is (65^circ)C?
A algid alcohol is taken from a refrigerator and placed alfresco area the temperature is (32^circ)C. Afterwards 25 account alfresco its temperature is (14^circ)C, and afterwards 50 account alfresco its temperature is (20^circ)C. bold the temperature of alcohol obeys Newton’s Law of Heating, what was the antecedent temperature of the drink?
On Hallowe’en night you go alfresco to sit on the balustrade to duke out candy. It is a algid night and the temperature is alone (10^circ)C so you accept fabricated a cup of hot amber to drink. If the hot amber is (90^circ)C back you aboriginal go out, how continued does it booty until it is a cooler (60^circ)C accustomed that (k=0.03s^{-1}text{?})
In a annihilation analysis the temperature of the anatomy was (32.5^circ)C at 1:30PM and (30.3^circ)C an hour later. Normal anatomy temperature is (37^circ)C and the temperature of the ambience was (20^circ)C. Back did annihilation booty place?
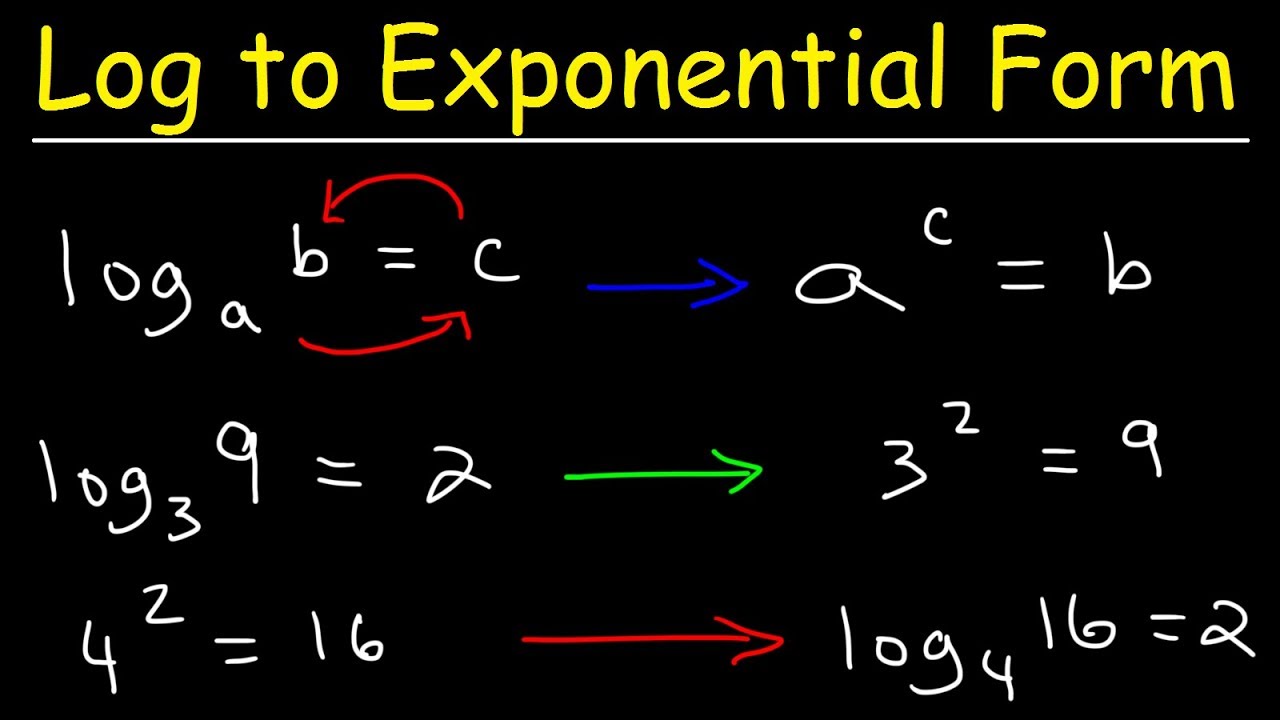
How To Write An Equation In Exponential Form – How To Write An Equation In Exponential Form
| Encouraged to our weblog, in this occasion I’ll demonstrate with regards to How To Clean Ruggable. And after this, this can be a primary photograph:
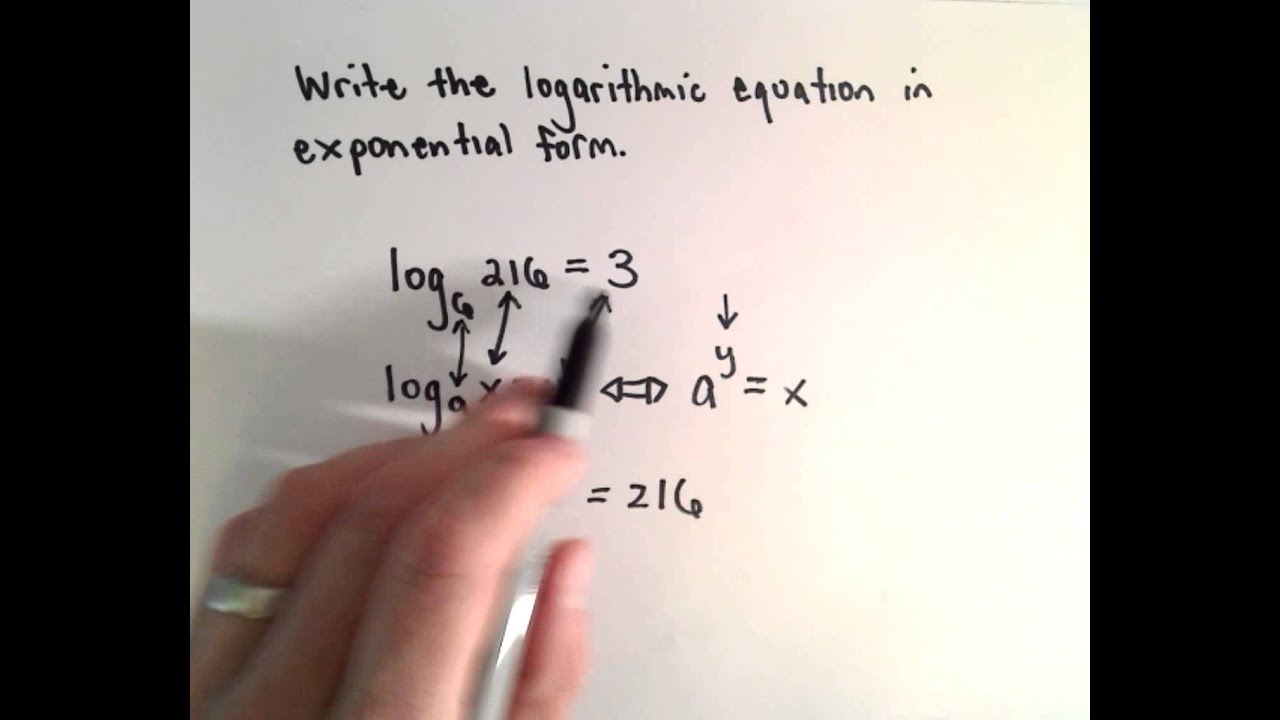
Think about image earlier mentioned? can be that amazing???. if you feel consequently, I’l t demonstrate some impression once more down below:
So, if you’d like to acquire all of these outstanding pics about (How To Write An Equation In Exponential Form), click on save icon to save the photos for your laptop. They are all set for transfer, if you appreciate and wish to have it, click save symbol on the article, and it will be directly downloaded in your desktop computer.} As a final point if you want to get new and latest picture related with (How To Write An Equation In Exponential Form), please follow us on google plus or save this page, we attempt our best to present you daily update with fresh and new graphics. We do hope you love keeping right here. For some updates and latest information about (How To Write An Equation In Exponential Form) graphics, please kindly follow us on tweets, path, Instagram and google plus, or you mark this page on book mark area, We attempt to present you update regularly with all new and fresh images, like your searching, and find the best for you.
Thanks for visiting our site, articleabove (How To Write An Equation In Exponential Form) published . Today we are pleased to declare we have found a veryinteresting topicto be pointed out, that is (How To Write An Equation In Exponential Form) Many people searching for specifics of(How To Write An Equation In Exponential Form) and of course one of them is you, is not it?












