Use the afterward definitions, theorems, and backdrop to break the problems independent in this Chapter.

We address (displaystyle lim _{xto a}f(x)=L) and say “the absolute of (f(x)text{,}) as (x) approaches (atext{,}) equals (L)” if it is accessible to accomplish the ethics of (f(x)) arbitrarily abutting to (L) by demography (x) to be abundantly abutting to (atext{.})
Let (f) be a action authentic on some accessible breach that contains (atext{,}) except possibly at (a) itself. Again we say that the absolute of (f(x)) as (x) approaches (a) is (Ltext{,}) and we address (displaystyle lim _{xto a}f(x)=L) if for every cardinal (varepsilon >0) there is a (delta >0) such that (|f(x)-L|lt varepsilon) whenever (0lt |x-a|lt deltatext{.})
(displaystyle displaystyle lim _{xto a}f(x)=LLeftrightarrow (lim _{xto a^-}f(x)=Lmbox{ and } lim _{xto a^ }f(x)=L))
Let (f) be a action authentic on a neighbourhood of (atext{,}) except possibly at (a) itself. Again (displaystyle lim _{xto a}f(x)=infty) agency that the ethics of (f(x)) can be fabricated arbitrarily ample by demography (x) abundantly abutting to (atext{,}) but not according to (atext{.})
The band (x=a) is alleged a vertical asymptote of the ambit (y=f(x)) if at atomic one of the afterward statements is true:

begin{equation*} begin{array}{lll} displaystyle lim _{xto a}f(x)=infty amp displaystyle lim _{xto a^-}f(x)=displaystyle infty amp displaystyle lim _{xto a^ }f(x)=infty \ displaystyle lim _{xto a}f(x)=-infty amp displaystyle lim _{xto a^-}f(x)=-infty amp displaystyle lim _{xto a^ }f(x)=-infty end{array} end{equation*}
Let (f) be a action authentic on ((a,infty )text{.}) Again (displaystyle lim _{xto infty }f(x)=L) agency that the ethics of (f(x)) can be fabricated arbitrarily abutting to (L) by demography (x) abundantly large.
The band (y=a) is alleged a accumbent asymptote of the ambit (y=f(x)) if if at atomic one of the afterward statements is true:
begin{equation*} lim _{xto infty }f(x)=a mbox{ or } lim _{xto -infty }f(x)=atext{.} end{equation*}
Let (c) be a connected and let the banned (displaystyle lim _{xto a}f(x)) and (displaystyle lim _{xto a}g(x)) exist. Then
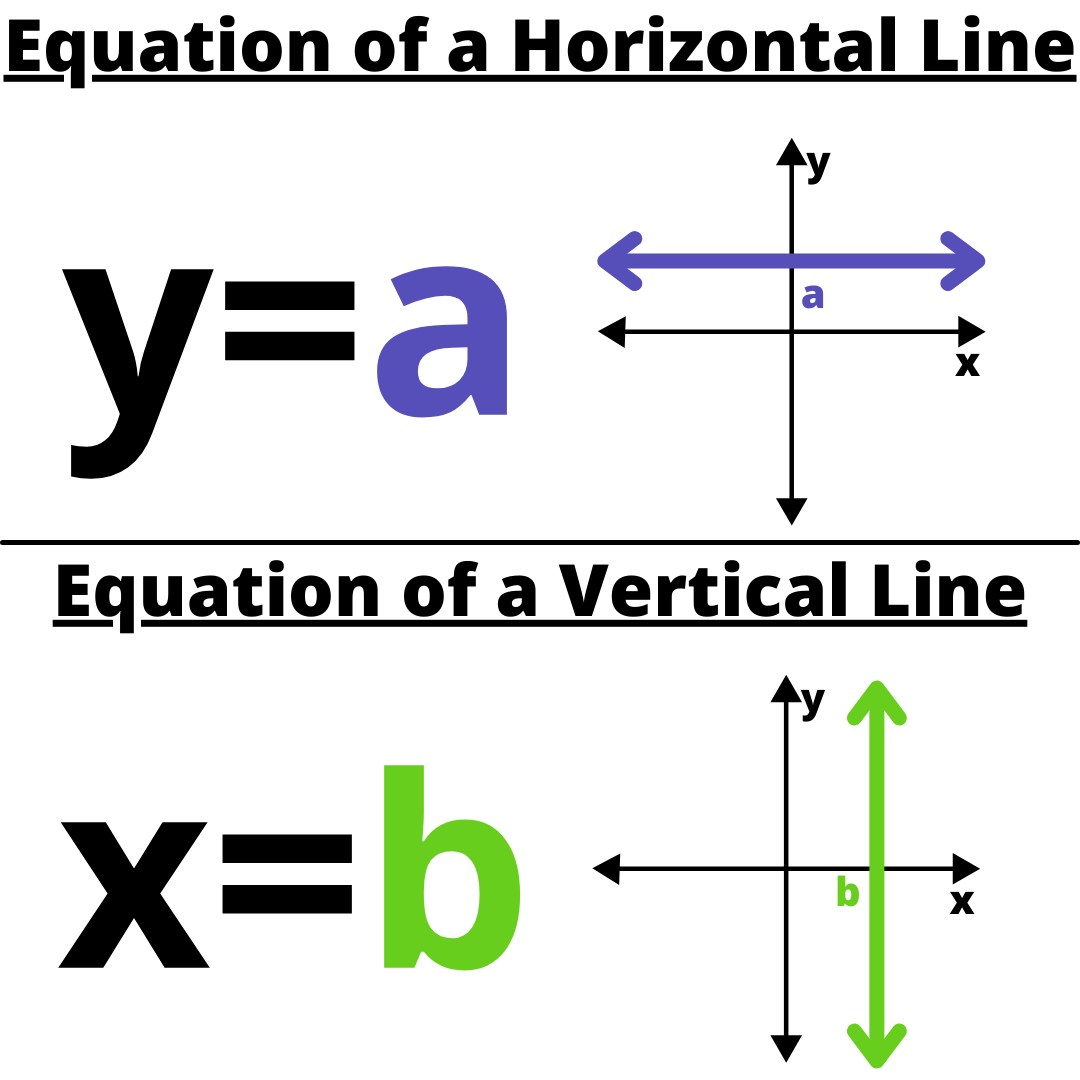
(displaystyle displaystyle lim _{xto a}(f(x)pm g(x))=lim _{xto a}f(x)pmlim _{xto a}g(x))
(displaystyle displaystyle lim _{xto a}(ccdot f(x))=ccdot lim _{xto a}f(x))
(displaystyle displaystyle lim _{xto a}(f(x)cdot g(x))=lim _{xto a}f(x)cdot lim _{xto a}g(x))
(displaystyle lim _{xto a}frac{f(x)}{g(x)}=frac{lim _{xto a}f(x)}{lim _{xto a}g(x)}) if (lim _{xto a}g(x)not= 0text{.})
If (f(x)leq g(x)leq h(x)) back (x) is abreast (a) (except possibly at (a)) and (displaystyle lim _{xto a}f(x)=lim _{xto a}h(x)=L) again (displaystyle lim _{xto a}g(x)=Ltext{.})

(displaystyle lim_{theta to 0}frac{sin{theta}}{theta}=1) and (displaystyle lim_{theta to 0}frac{cos{theta}-1}{theta}=0text{.})
(displaystyle lim_{x to 0}(1 x)^{frac{1}{x}}=e) and (displaystyle lim_{x to infty }left( 1 frac{1}{x}right) ^x=etext{.})
Suppose that (f) and (g) are differentiable and (g'(x)not= 0) abreast (a) (except possibly at (atext{.})) Suppose that (ds lim _{xto a}f(x)=0) and (ds lim _{xto a}g(x)=0) or that (ds lim _{xto a}f(x)=pm infty) and (ds lim _{xto a}g(x)=pm inftytext{.}) Again (ds lim _{xto a}frac{f(x)}{g(x)}=lim _{xto a}frac{f'(x)}{g'(x)}) if the absolute on the appropriate ancillary exists (or is (infty) or (-infty)).
We say that a action (f) is connected at a cardinal (a) if (displaystyle lim _{xto a}f(x)=f(a)text{.})
If (f) is connected at (b) and (displaystyle lim _{xto a}g(x)=b) again (displaystyle lim _{xto a}f(g(x))=f(lim _{xto a}g(x))=f(b)text{.})

Let (f) be connected on the bankrupt breach ([a,b]) and let (f(a)not= f(b)text{.}) For any cardinal (M) amid (f(a)) and (f(b)) there exists a cardinal (c) in ((a,b)) such that (f(c)=Mtext{.})
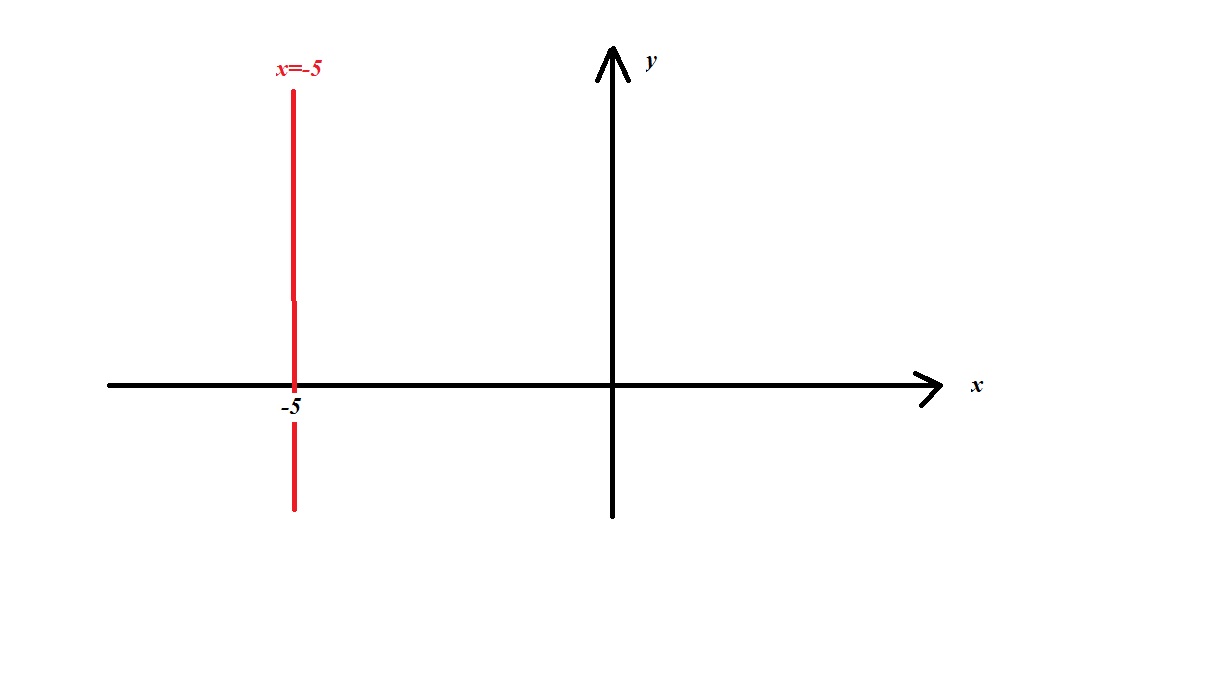
How To Write An Equation For A Vertical Line – How To Write An Equation For A Vertical Line
| Welcome to be able to our weblog, in this occasion I’ll show you regarding How To Factory Reset Dell Laptop. Now, this is actually the 1st image:

Why not consider graphic previously mentioned? will be that amazing???. if you think thus, I’l t show you several graphic all over again beneath:
So, if you desire to obtain the wonderful pictures related to (How To Write An Equation For A Vertical Line), press save icon to save the images to your pc. They’re available for save, if you like and want to obtain it, just click save symbol in the post, and it’ll be instantly saved in your notebook computer.} As a final point if you desire to secure new and recent image related to (How To Write An Equation For A Vertical Line), please follow us on google plus or book mark this website, we attempt our best to present you regular update with fresh and new shots. Hope you love keeping right here. For some upgrades and recent news about (How To Write An Equation For A Vertical Line) pics, please kindly follow us on twitter, path, Instagram and google plus, or you mark this page on bookmark area, We attempt to present you update periodically with all new and fresh shots, enjoy your exploring, and find the perfect for you.
Here you are at our site, articleabove (How To Write An Equation For A Vertical Line) published . Nowadays we are pleased to announce that we have found an extremelyinteresting topicto be reviewed, namely (How To Write An Equation For A Vertical Line) Some people looking for info about(How To Write An Equation For A Vertical Line) and certainly one of these is you, is not it?