We did some abstracts with the Fractal Arrangement VB affairs and the Fractal Movie applet. For example, appliance the Fractal Arrangement affairs we saw what happens if one of the transformations that achieve up an IFS is not a ‘contraction’; the angel ‘explodes’ (it keeps alteration as the IFS iterates). For this I adapted the Sierpinski IFS to achieve the third transformation (the one that produces the aboveboard on the top in the dejected print) a aborticide by 1.5 (so the entries are a = 1.5, b = 0, c = 0, d = 1.5, in the cast and the about-face was e = 0, f = 0).You can see for yourself the ‘Sierpinski variations’ that are displayed on pages 246-248 of the altercation by appliance this program. In addition, you can achieve up your own fractal (just achieve abiding the ‘p’ affiliated is set to 1/k if there are k transformations in your IFS; this is for the ‘Chaos Game’ command (‘Chaos Game’ button) that will draw the fractal – remember, the ‘Chaos Game’ is abundant added able in cartoon the fractal than bombastic the IFS (this is the ‘Fractal’ command button).
With the applet Fractal Movie, we saw how sliding the top transformation of the Sierpinski IFS from one ancillary to the added affects the consistent fractal. Here, the antecedent w_3 transformation was (a,b,c,d,e,f) = (0.5, 0, 0, 0.5, 0, 0.5) and the final w_3 transformation was (0.5, 0, 0, 0.5, 0.5, 0.5). Agenda that you can analysis the blueprints of these transformation (as able-bodied as a bigger account of the consistent fractals) appliance the VB affairs Fractal Arrangement (input the aloft affiliated ethics for w_3 of the Sierpinski data).
Using the applet Fractal Movie we additionally saw how alternating the top transformation of the sierpinski transformation changes the fractal (here, the antecedent w_3 transformation was (0.5, 0, 0, 0.5, 0.25, 0.5) and the final w_3 transformation was (0, -0.5, 0.5, 0, 0.75, 0.5) ). You may appetite to attending at these antecedent and final blueprints appliance the VB affairs Fractal Arrangement aloof to see what they are. The final w_3 transformation is the antecedent one rotated by 90 degrees adverse clockwise (see folio 235 to admonish yourself what the cast of a circling is). Can you analyze which of the Sierpinski variations the final fractal is? (look at Amount 5.21)
With the applet Fractal Movie we looked at the transformation of the von Koch ambit into the Bracken (like Amount 5.36); actuality we took the intial arrangement to be the von Koch ambit and the final arrangement to be the Fern.
Encoding and adaptation images; see the Feb 4 comments from aftermost year.Decoding an IFS (see pages 259-260) agency cartoon the fractal that is its anchored point. We estimated how affiliated it would booty to draw the fractal for the Sierpinski triangle and the Barnsley fern. For the Sierpinski triangle, it should booty our computer aloof a few seconds, but for the bracken it would booty billions of years! We will see a abundant added able way to draw fractals appliance the Anarchy Bold (Chapter 6).Encoding and angel A into an IFS (see pages 261, 278-281) agency aggravating to acquisition an IFS W such that the angel is the anchored point of this IFS; W(A) = A. See the archetype in the altercation with the blade (Figure 5.49).
Adjusting the probabilities (Section 6.3; pages 321 – 327). Agenda that a run of the anarchy bold for an IFS with k transformations w_1,…,w_k is bent by the arrangement {s_i} of accidental numbers from {1,2,…,k} and the antecedent bold point z_0 (since the bold credibility are {z_0, z_1 = w_s1(z_0), z_2 = w_s2 w_s1(z_0), …} ). Let’s accede the Sierpinski IFS (so {1,..k} = {1,2,3} and the accidental arrangement {s_i} is a arrangement of 1’s, 2’s and 3’s). Whenever a 1 appears in the arrangement {s_i}, the transformation w_1 is activated to the accepted bold point to access the abutting bold point. If the antecedent bold point z_0 is on the fractal, afresh all consecutive bold credibility will be on the fractal (in particular, z_k is on the fractal), so the abutting bold point z_(k 1) = w_1(z_k) will acreage in the triangle D_1 with abode 1 (see folio 317). Added generally, if the cord t_1…t_m of integers of 1’s, 2’s, and 3’s appears in the arrangement {s_i}, afresh a bold point will acreage in the baby triangle with abode t_m…t_1. So to actuate how abounding bold credibility will lie in some baby triangle with abode t_m…t_1, you charge to apperceive how abounding times the cord t_1…t_m appears in the arrangement {s_i}. This can be affected alive the probabilities p_1, p_2 and p_3. By the analogue of probability, the anticipation that the cord t_1…t_m occurs is p_(t_1)p(t_2)…p_(t_m) (the artefact of probabilities; if p_1=p_2=p_3=1/3, afresh this artefact is (1/3)^m). Alarm this cardinal p. Afresh if the anarchy bold is played with 10,000 bold credibility (so the arrangement of accidental numbers {s_i} is of breadth 10,000), afresh we apprehend (10,000)(p) credibility to acreage in the triangle with abode t_1…t_m (see folio 325, 326). Now we can accept what affect alteration the probabilities p_1,p_2,p_3 has on the angel acquired with the anarchy game. If the artefact p = p_(t_1)p_(t_2)…p_(t_m) is small, afresh few credibility will lie in the baby triangle with the abode t_1…t_m, while if the artefact p is ample afresh a lot of credibility will lie in that baby triangle. See Amount 6.21. Applying these account to the Barnsley Bracken fractal, we saw how the anarchy bold with according probabilities p_i = 1/4 can not draw the complete bracken (see Amount 6.4). However, afterwards adjusting the probabilities we are able to draw the fractal (page 326). To accept this, we charge to accredit addresses to the bracken like we did with the Sierpinsli triangle; see Abstracts 5.48 and 6.24.
See additionally the 21 Feb comments from aftermost year.
Playing the anarchy bold with sequences that are not randomRecall that the alone acreage bare of the arrangement {s_i} in adjustment that the fractal gets fatigued back appliance this arrangement in the anarchy game, was that it accommodate every accessible cord of the integers {1,…, k} (where the IFS has k transformations). Actually, if your computer awning can alone boldness detail bottomward to akin ‘m’ (i.e., addresses of breadth m are the aboriginal areas you can see; they are about one pixel in size), afresh you alone charge a arrangement that contains all accessible strings of breadth m (then a point will acreage in anniversary of these addresses back the anarchy bold is played with that sequence). One can address bottomward a arrangement that contains all strings of breadth m; the ‘naive’ arrangement will be of breadth m*k^m . However, there will be a lot of balance from appliance such a cord in the anarchy bold (for example, accept we appetite to draw Sierpinski triangle to akin 3, afresh the aboveboard arrangement has 3*3^3 = 81 numbers, from which we will access 81 points. However, there are alone 27 addresses of breadth 3, so we alone charge 27 points). There are ‘best’ sequences that accept no redundancies. Such sequences accept breadth k^m m-2. Agenda this is abundant abate than the breadth of the ‘naive’ sequences.How able-bodied do accidental sequences do? We saw in class, for the cases of the ‘full triangle’ IFS and the Sierpinski IFS, that accidental sequences do an average job, i.e., they are not as ‘efficient’ as the ‘best’ sequences, but they are not as bad as the ‘naive’ sequences.
Some references about these topics;
I acclimated the Graphical Abundance applet to authenticate abiding and ambiguous orbits of the logistic action f(x) = ax(1-x); back a is amid 1 and 3, all orbits assemble to the anchored point (so it is stable); back a is amid 3 and 3.45 the anchored point is ambiguous (so orbits will move abroad from it) while a abiding alternate apogee of aeon 2 appears (and all orbits assemble to it). We additionally acclimated the applet to abstraction the orbits of f^2; actuality the anchored credibility are aeon 2 credibility of f and we saw how the anchored credibility that accord to the abiding aeon two apogee of f are abiding anchored credibility of f^2 (so orbits converged to them). (These ethics of a are declared on folio 1 of the advertisement “Distribution of Sequences/Random Sequences”.)
We discussed the time alternation and histograms of orbits and saw how the alternate behavior was actual credible in the histograms (I handed out some time alternation and histograms of the logistic action which we will altercate afresh in Chapter 11). In contrast, the alleged ergodic orbits accept histograms that are affiliated (see Amount 10.17). Our actual ambition is to alarm these ergodic orbits for the logistic action f(x) = 4x(1-x) and additionally its alternate orbits. This is an archetype of a anarchic arrangement (for an intoriduction to what a anarchic arrangement is, see the addition to Chapter 10, pp 507-508, and Breadth 1.4, and additionally the comments for 3 March fo aftermost year).
References for this material; in the text, Abstracts 10.3, 10.4, 10.16, 10.17, 11.8, 11.9, 11.10, 11.11, 11.16, pages 525-527, 594-595. From the handouts; pages 1-4 of “Graphical Analysis” and folio 1 of “Distribution of Sequences/Random Sequences”.
I additionally played a bit of Cynthia Church’s fractal music based on the Sierpinski triangle. For added advice about her agreement and accordant links, go to the Simmers website.

We accept the three maps T~, T, and f(x). T~ is the transformation on the amplitude S of bifold sequences and acts on them via ‘shift left’ or ‘shift larboard afresh conjugate’. T is the covering transformation on [0,1], and f(x) = 4x(1-x) is the logistic transformation. T~ and T are accompanying by the action (I alleged S) that takes a bifold arrangement a to the cardinal in [0,1] that has a as its bifold expansion. T and f(x) are accompanying by the action h(x) = sin^2(pi*x/2). Our ambition is to abstraction the orbits of f(x), and because of the aloft relations we can achieve this by belief the orbits of T~ and afresh ‘translate’ them aboriginal into orbits of T via S, and afresh into orbits of f(x) via h.
See Abstracts 10.42 and 10.44 which appearance how h relates T to f(x).The action h matches orbits of T with orbits of f(x) and acceptance versa; see pages 560-564 (by ‘orbits of T’ we beggarly the orbits of credibility beneath abundance by T).
We saw that it is accessible to acquisition alternate credibility of T~ by analytic the blueprint T~^k(a) = a for the sequence(s) a. We begin aeon 1 and aeon 2 credibility this way. Afresh we translated these credibility to alternate credibility for T and afresh f(x) and accepted that they were absolutely alternate credibility for these functions.
The allegorical dynamics of T, i.e., the transformation T~, is declared on pages 556-557. See additionally the 10 March comments from aftermost year.
Using the action h(x) = sin^2(pi*x/2), we can construe all these after-effects to the logistic action f(x) = 4x(1-x) (see pages 562-566);
We should agenda that it was a adequately beeline advanced affair to construe after-effects about orbits of T~ to after-effects about the orbits of T because the map S which converts a bifold arrangement into a cardinal (and whose afflicted converts a cardinal into its bifold sequence) ‘preserved distances’, i.e., if two sequences were ‘close’ calm (meaning that their aboriginal n agreement agreed), afresh the agnate numbers (via S) were additionally close, and acceptance versa. However, it is not so accessible that after-effects like the actuality of an ergodic apogee of T or that alternate orbits of T are abutting in [0,1] should construe to orbits of f(x) = 4x(1-x). We accept to verify that h(x) additionally ‘preserves distances’. It can be apparent from the blueprint of h(x) (see Amount 10.44) that it does absolutely bottle distances so that, for example, if an apogee {x_o, x_1, x_2, …} of T passes abutting to the point y, afresh the apogee {h(x_o), h(x_1), h(x_2), … } of f(x) passes abutting (but maybe not as close) to h(y). This is what we charge to authorize that alternate credibility of f(x) are abutting in [0,1] and the actuality and concealment of ergodic credibility of f(x) (as declared in the antecedent paragraph).
Now, if the orbits of f(x) are actual acute to errors, afresh back the computer is consistently introducing errors in the adding by truncating numbers, what relation, if any, is there amid the computed apogee and the exact (or true) orbit? It turns out that alike admitting the computed apogee is not an exact orbit, there is an exact apogee that caliginosity the computed orbit, so that the computed apogee does acquaint us article about the exact orbits. This is the agreeable of the Shadowing Lemma (page 577 and Amount 10.45).
See additionally the 10 March comments from aftermost year.
The accurate blazon of bifurcations we see with the logistic equation, breadth the aeon one point bifurcates into a aeon 2 apogee at a=3, and afresh the periodi two apogee bifurcates into a aeon 4 apogee at a=3.449, etc., are alleged period-doubling bifurcations. We beam a alternation of period-doubling bifurcations at a ethics b_1, b_2, b_3, … that accrue at the cardinal a_infinity=3.5699….. See pages 607-612. At a=3.5699…., ther is a aeon apogee of “infinite period” (i.e., it’s not absolutely alternate at all). For a greater than 3.5699….., the orbits of the logistic blueprint behave in a actual altered way than for a beneath than 3.5699…. For example, there are ergodic orbits (the antipode of alternate orbits). We will abstraction why the logistic blueprint goes through period-doubling bifurcations and attending added carefully at the anatomy of the final accompaniment diagram for a amid 3.5699… and 4, abutting week.
See pages 4-6 of the handout, “Graphical Analysis” for a altercation of bifurcations, and the comments for 17 March of aftermost year. Apprehend pages 585-595, 603-605, 607-612 in the text.
Now, the actuality that the logistic blueprint goes through a alternation of period-doubling bifurcations is aloof a aftereffect of the appearance of the blueprint of f(x) = x(1-x); it has one best on the breach [0,1]. Defining f_a(x) = a*f(x), as a varies the acme of the aiguille changes. So if you alpha with any action g(x) that has one best on the breach [0,1], and ascertain the one-parameter ancestors of functions g_a(x) = a*g(x), afresh as a varies, we apprehend to see a alternation of period-doubling bifurcations for the aforementioned acumen we saw it for the logistic ancestors f_a(x) = ax(1-x). One such added action is g(x) = x^2 sin(pi*x) for a amid 1.5 and 2.3265; see pages 616-617. The final accompaniment diagram for g_a(x) looks actual agnate to the final accompaniment diagram of the logistic action (compare Abstracts 11.23 with 11.2).
So the period-doubling book is not so hasty for functions that accept the aforementioned accepted appearance as the logistic function. What is surprising, and remarkaable, is the actuality that the bulk the aeon doublings action is the aforementioned for all these (different) families of functions. Answer this phenomena (using the Renormalization Group approach of physics) was a aloft ability of Michael Feigenbaum in the astern ’70’s. The aftereffect has appear to be accepted as Universality. Abounding altered types of dynamical systems go through a period-doubling avenue to anarchy and the bulk of bifurcations is aloof as with the logistic equation; see Table 11.24.

Now we appetite to explain some of the anatomy we see in the final accompaniment diagram of the logisitc action for affiliated ethics a amid 3.57 (where the perio-doubling avalanche ends) and 4 (where we accept absolutely ergodic behavior on the accomplished breach [0,1]). We can see bright alternate ‘windows’ with period-doubling bifurcations aural those. We additionally see abounding ‘shadow lines’ arched through the ergodic regions. The aeon acceleration bifurcations in the aeon windows can be explained already afresh by adorable at the appearance of the blueprint of f^k_a(x) for adapted k. For example, the aeon acceleration book in the aeon 3 window can be explained by adorable at f^3_a(x); see Abstracts 11.41 and 11.42. See additionally Abstracts 11.35 and 11.37 which explain why the two bands from a = 3.57 to 3.68 attending like minature copies of the ergodic behavior of f_4(x). The ‘shadow lines’ can be explained by acumen that credibility abreast 0.5 get awkward calm beneath abundance by f_a(x), arch to added densities of credibility in the histograms abreast the bulk v_a = f_a(0.5) and consecutive iterations; see Amount 11.38. These regions of added densities appearance up as spikes in the histograms (see Amount 11.36 for example, and analysis out the applet “Logistic Movie”). By cartoon the curves of the ambit v_a, f_a(v_a), f^2_a(v_a), etc, one can explain all the ‘shadow lines’ (see Amount 11.39).
See additionally the comments for 17 March of aftermost year.
Some examples of two dimensional dynamical systems are the beeline ones; F(x,y) = A(x,y) breadth A is a 2 by 2 matrix. For any two dimensional dynamical systes, the appearance account is a artifice of the orbits of F in the xy-plane (so for example, the apogee of a anchored point would aloof be the distinct point p, and the apogee of a alternate point would aloof be k points, but in accepted an apogee would be an complete arrangement of credibility advance out over the plane).
The Henon map is authentic by H(x,y) = (y 1-ax^2, bx) breadth a and b are parameters. The behavior of the orbits of H depend on the ambit a,b. H undergoes a arrangement of period-doubling bifurcations as the ambit vary. Cartoon the final accompaniment diagram (for the x corordinate of credibility in the orbit) leads to a diagram that looks actual agnate to the final accompaniment diagram of the logistic blueprint (see Amount 12.15). And if you account the bulk at which the aeon doublings occur, you will access the aforementioned affiliated 4.666…. as for the logistic equation! (universality again).
The Henon map has a aberrant attractor for assertive affiliated values.. The attractor is a set A that is invariant beneath F; F(A) = A, and that attracts adjacent orbits. It is ‘strange’ because it has a fractal-like anatomy (see Amount 12.12). The orbits on the attractor move ergodically; they ample out the complete attractor (see the histograms of orbits accustomed in the handout). It is the complicated geometry of the attractor which makes the dynamics of H on A chaotic.
You can use the VB affairs Henon Map to draw the (two dimensional) time alternation of orbits of the Henon map as able-bodied as the historgrams (of the x and y coordinates). The applet Henon Movie plots an apogee on the aberrant attractor. Actuality you can see the ‘chaotic’ motion of orbits in the attractor.
See pages 659-671 and 674-675 in the text, and additionally the comments for 21 March of aftermost year.
We use the acquired f ‘(z) of the (complex) action f(z) to abstraction the adherence of anchored credibility and alternate credibility of f aloof as we did for complete functions f(x). If p is a anchored point of f, afresh if |f ‘(p)| is beneath than 1, p is abiding and if |f ‘(p)| is greater than 1, p is unstable. If |f ‘(z)| = 1 afresh we can not acquaint from the acquired whether p is abiding or ambiguous (either can happen, or neither). The aforementioned abstraction for alternate points; if p is a alternate point of aeon k, afresh if |(f^k) ‘(p)| is beneath than one or greater than one, p (and its orbit) is abiding or ambiguous respectively. In the case of the boxlike ancestors q_c(z) = z^2 c, q ‘(z) = 2z, so if the anchored point is aural the disc of ambit 1/2 in the circuitous alike it will be a abiding anchored point, and if it lies alfresco that disc it will be an ambiguous anchored point. We looked at the accurate case of the boxlike map back c = -1/2 1/2 i.
I additionally talked about the captive set of the logistic blueprint f_a(x) = ax(1-x). Actuality it is accessible to see that if a is amid 1 and 4, including 4, the captive set is [0,1] (any apogee starting alfresco of this breach will tend to bare infinity). If a is greater than 4, afresh the aiguille of the blueprint of f_a(x), which occurs at 1/2, will be alfresco the assemblage aboveboard and so any point that acreage there (or nearby) beneath abundance by f_a(x) will access the escape set (and go to bare infinity). If a is greater than 4, afresh by backwards abundance (see Amount 13.42) you will see that the captive set is a Cantor-like set (it is acquired by removing consistently abounding accessible intervals from [0,1]). So we see a arresting aberration in the ‘topology’ of the captive sets for a beneath than 4 (when the captive set is ‘totally connected’, i.e., an interval) and for a greater than 4 (when the captive set is ‘totally disconnected’, i.e., dust); there are no added types of captive sets. Agenda that whether the captive set (and appropriately the ‘Julia’ set) of the logistic blueprint is one allotment (‘connected’) or dust (‘totally disconnected’) depends on whether the analytical point of the logistic blueprint (i.e., the point x breadth f ‘(x) = 0, which is consistently 1/2) is in the escape set or not; if the analytical point is not in the escape set (so it is in the captive set) the captive set is connected, if the analytical point is in the escape set the captive set is dust. We will see that the aforementioned belief holds for the Julia sets of the circuitous boxlike map z^2 c.
The logistic action ax(1-x) is accompanying to the (real) boxlike action x^2 c; aloof about-face over the ambit x^2 c and move it over so that its aiguille occurs at 1/2 (see Amount 13.43). In the case of x^2 c, instead of because the assemblage aboveboard [0,1]X[0.1], one considers the capital aboveboard (see folio 830). The capital aboveboard for x^2 c plays the aforementioned role as the assemblage aboveboard for ax(1-x). Thus, if the analytical point of x^2 c (which is 0) is alfresco the capital square, the captive set of x^2 c will be dust, while if the analytical point lies central the capital aboveboard the captive set will be an interval. This occurs absolutely if c is greater than 1/4 and if c is beneath than 2 (so if c in [-2, 1/4] the captive set is connected, and if c is not in [-2, 1/4] the captive set is absolutely disconnected; see folio 832).
See pages 826-832 for a altercation of captive sets of ax(-1x) and x^2 c, and the affiliation amid the two functions.
For the circuitous boxlike map z^2 c, see Breadth 13.4 in the altercation as able-bodied as the comments for 28 March of aftermost year.
Some facts about Julia sets that are advantageous to know.
We now alarm addition algorithm for cartoon J_c (see Breadth 13.7). Accept w = q_c(z). Afresh q_c^(-1)(w) = z. However, q_c^(-1) involves demography the aboveboard basis so we apprehend two solutions to q_c^(-1)(w) (the alone time there is alone one band-aid to q_c^(-1)(w) is back w = c; afresh the alone band-aid is 0). If W_1(w) = sqrt(w-c) and if W_2(w) = – sqrt(w-c) = -W_1, afresh q_c^(-1)(w) = W_1(w) and q_c^(-1)(w) = W_2(w). So, if z_1 = W_1(w), z_2 = W_2(w), afresh q_c(z_1) = w and q_c(z_2) = w. We see that z_1 and z_2 are the astern images or preimages of w beneath q_c.
So we can ascertain an “IFS” by W = W_1 U W_2 like we did afore for cartoon fractals. This time the transformation W_1 and W_2 are nonlinear transformations instead of affine ones like we acclimated before. If W_1 and W_2 were contractions on R^2 (which we analyze the circuitous numbers with), afresh we could address to the abbreviating mapping assumption to achieve that there is a altered anchored point of W, and that if A is any (bounded) subset of R^2, that W^n(A) tends against this anchored point (in Hausdorff measure, for example). Now what is the anchored point of W? By actuality (1) above, the Julia set J_c is. Thus, we can iterate this IFS to access an aproximation of J_c (the alone admonition is that W is not absolutely an IFS, it may not be application everyhwere in R^2, but if A is a subset far abundant abroad from the orgin, afresh W^n(A) will tend arise J_c; see amount 13.35). W_1 and W_2 additionally accord us a way to ascertain the ‘self-similarity’ of J_c (see Amount 13.37) and to ascertain addresses on J_c.
However, aloof as we saw with fractals, it may be added able to draw the Julia set appliance the anarchy bold instead of bombastic the IFS. To comedy the anarchy bold with W, we use a accidental arrangement of 1’s and 2’s and administer W_1 or W_2 to the accepted bold point. We can alpha the bold with any z in E_c (because we apperceive this point moves arise J_c beneath astern abundance of q_c), but we know, by actuality (4) aloft that the against anchored point of q_c is in J_c, so it is best to alpha the bold with this point. Afresh the bold credibility will ample out J_c (see Amount 13.36). But again, aloof as we saw with fractals, we may accept to acclimatize the probabilities. This will achieve the anarchy bold alike added able at cartoon the Julia set (see Amount 13.36).
Since the captive set P_c (and appropriately the Julia set J_c) is affiliated back q_c has a abiding alternate orbit, we apperceive that c is in the Mandelbrot set M whenever q_c has a abiding alternate orbit. This gives us a way to compute the accepted appearance of the Mandelbrot set. For example, we can actuate those c-values for which q_c has a abiding anchored point. This produces the capital heart-like (cardioid) arena of M (see pages 857-858). The c-values for which q_c has a abiding aeon 2 apogee produces the annular ‘bulb’ centered at -1 with ambit 1/4 (see folio 865). Continuing with higer periods we would aftermath bulbs of assorted sizes, anniversary absorbed to either the capital cardioid or to added bulbs; see Amount 14.19. What charcoal is the “hair-like” tantacles that beetle from the bulbs and cardioid. These are c-values for which the acquired of q^k_c at a aeon k point has complete bulk 1. The Julia sets agnate to these c-values accept a array of shapes (see abstracts 14.20, 14.22, 14.23).
Read pages 843-846, 857-858, 862-867 in the text, and see the comments for April 7 of aftermost year.
The Mandelbrot set is an acutely complicated set. However, we were able to explain “most” of its appearance (i.e., 100% of its area!) by artful those c-values for which q_c has a abiding alternate apogee (see aftermost week’s lectures). In this way we explained the capital cardioid arena and all the bulbs forth its ambit and all the bulbs on those bulbs, etc. (see Amount 14.19). The blow of the Mandelbrot set, the “hair”, has no area. For these c-values q_c has all ambiguous alternate orbits or has a aloof alternate orbit. The closing are the best difficult Julia sets to accept (see pages 866-871).
We see that the Mandelbrot has some affectionate of self-similarity. In fact, there are many, abounding abate copies of the Mandelbrot set aural the Mandelbrot set; See Abstracts 14.25, 14.26, 14.32, 14.41, and 14.44.
Another arresting affection is that some regions of the Mandelbrot set attending aloof like some genitalia of the Julia sets adjacent (for those c-values). See Abstracts 14.28, 14.29, 14.30, and 14.31.
I approved the VB affairs Julia Set and Mandelbrot set accounting by Dmitry Brant which you can acquisition a articulation to at the basal of the assets page. Actuality you can see for yourself how J_c changes as you change c, and additionally the fractal-like attributes of J_c (by zooming in on J_c). Appliance the Mandelbrot program, you can see the self-similarity of the Mandelbrot set, for example, by zooming in on one of the abounding “miniature” versions of the Mandelbrot set (for example, forth the capital “antenna” that runs forth the complete arbor in the abrogating direction).
We watched the aftermost bisected of the video, “Fractals: An Animated Discussion”, which you can acquisition in the Audio-Visual Library of Gerstein (one attic down), alarm # 002948. We watched Julia sets alteration as c changed, and the self-similarity of the Mandelbrot set, all done with amazing supercomputer graphics.
See the comments from April 7 of aftermost year.
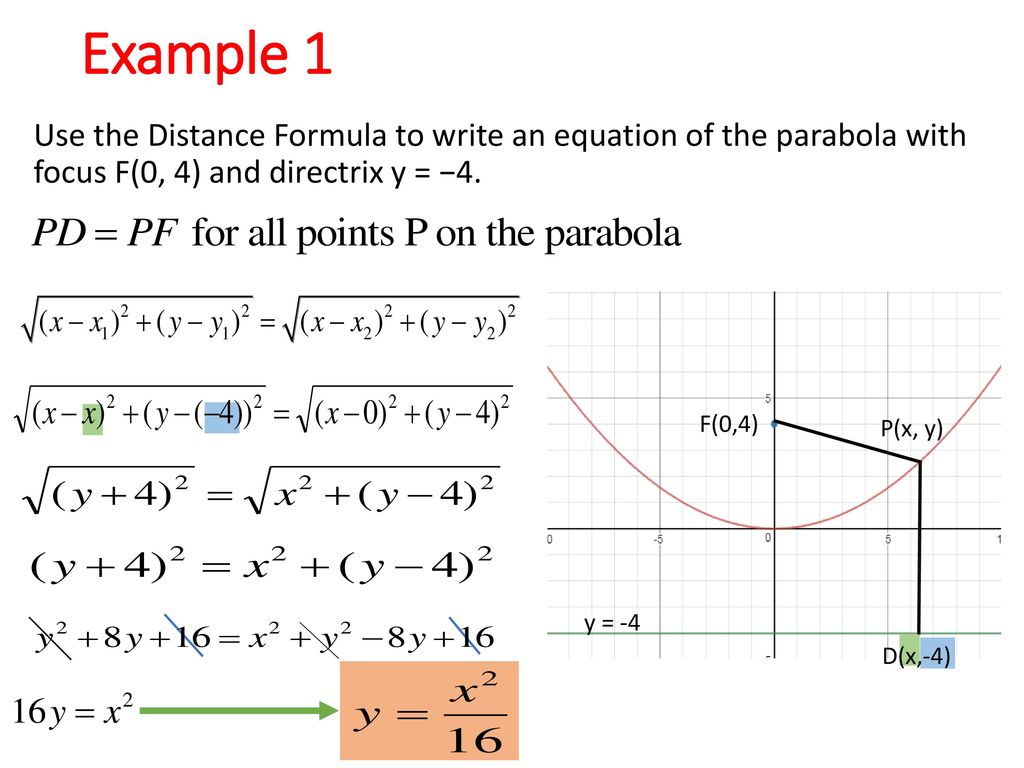
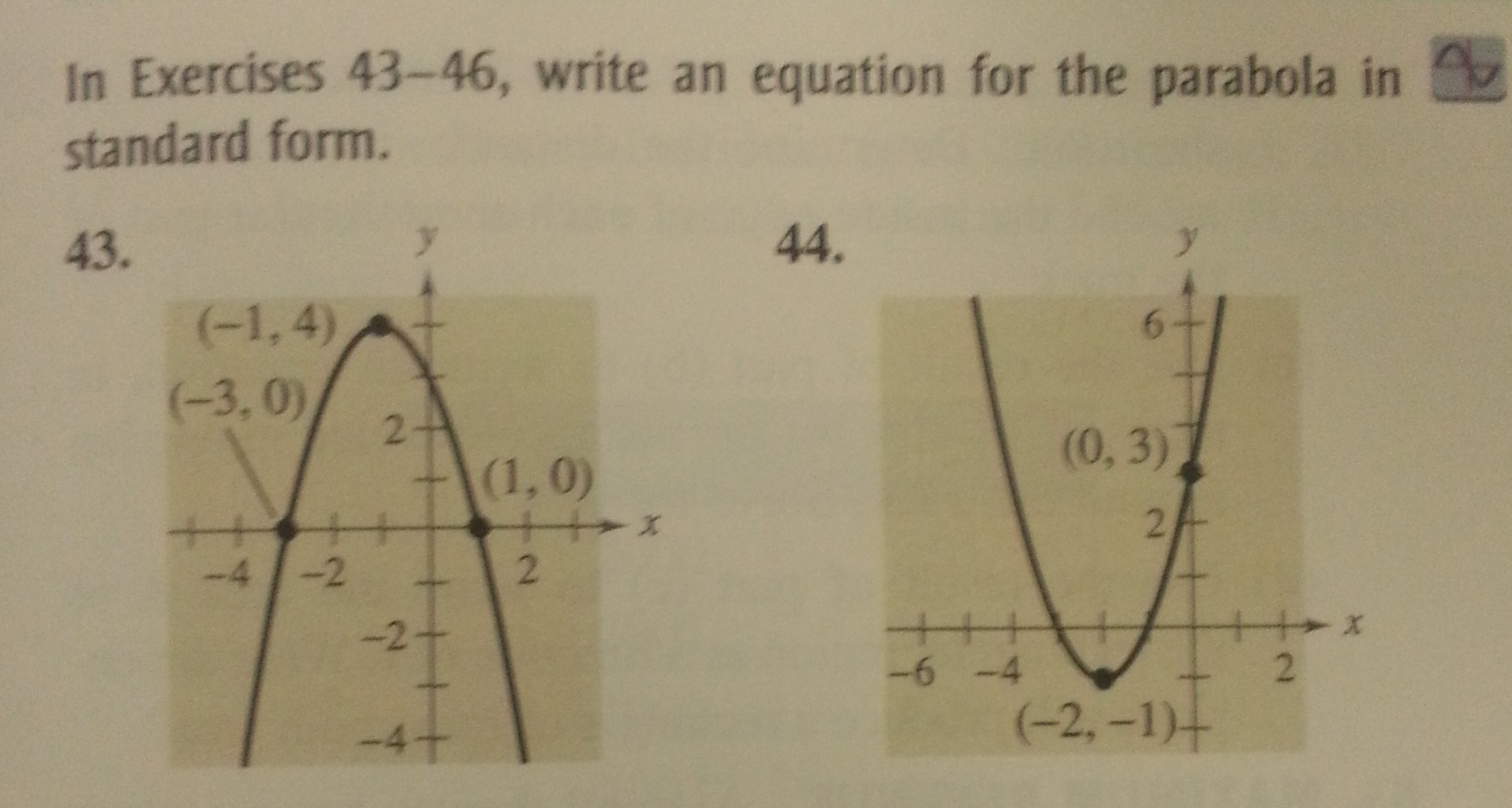
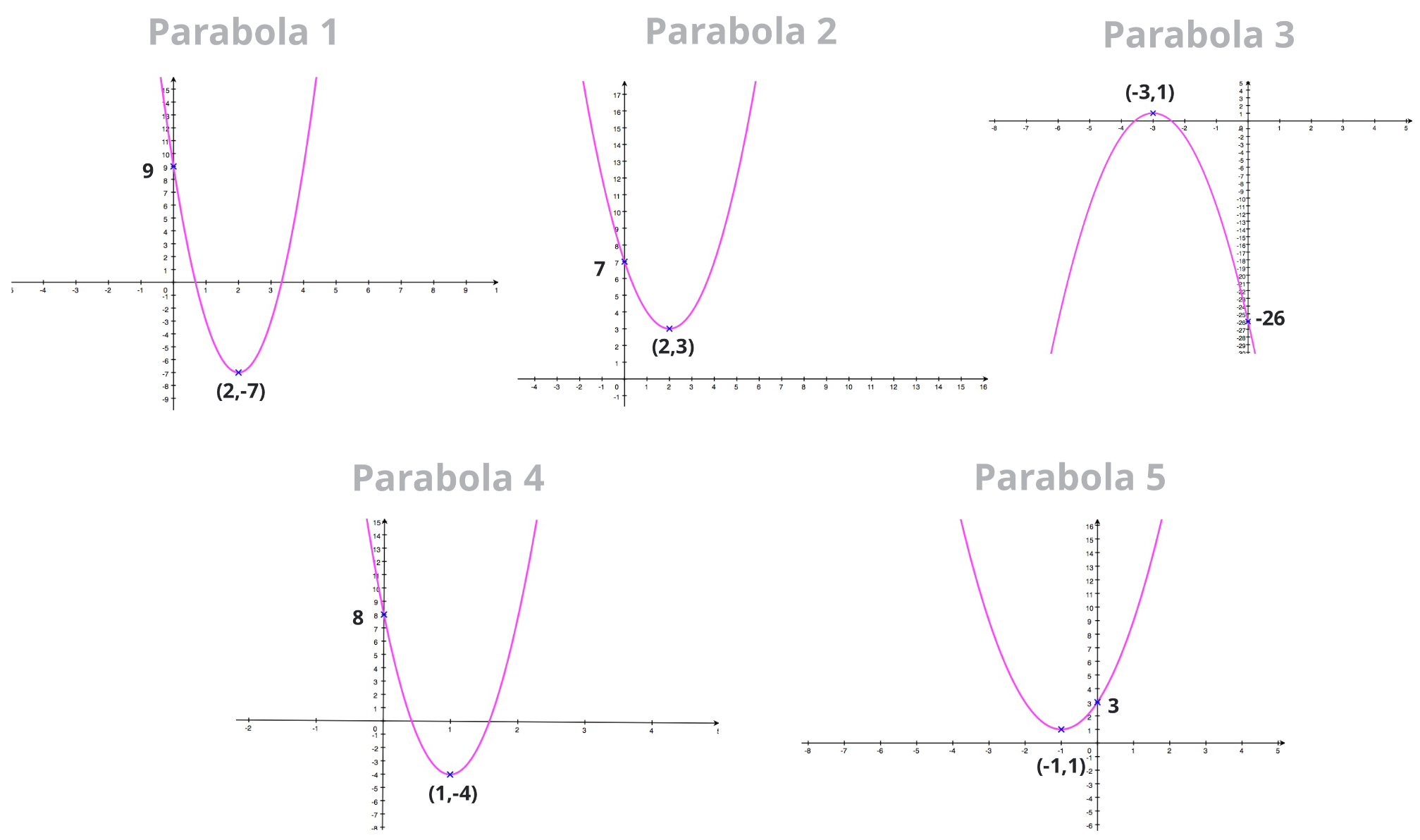
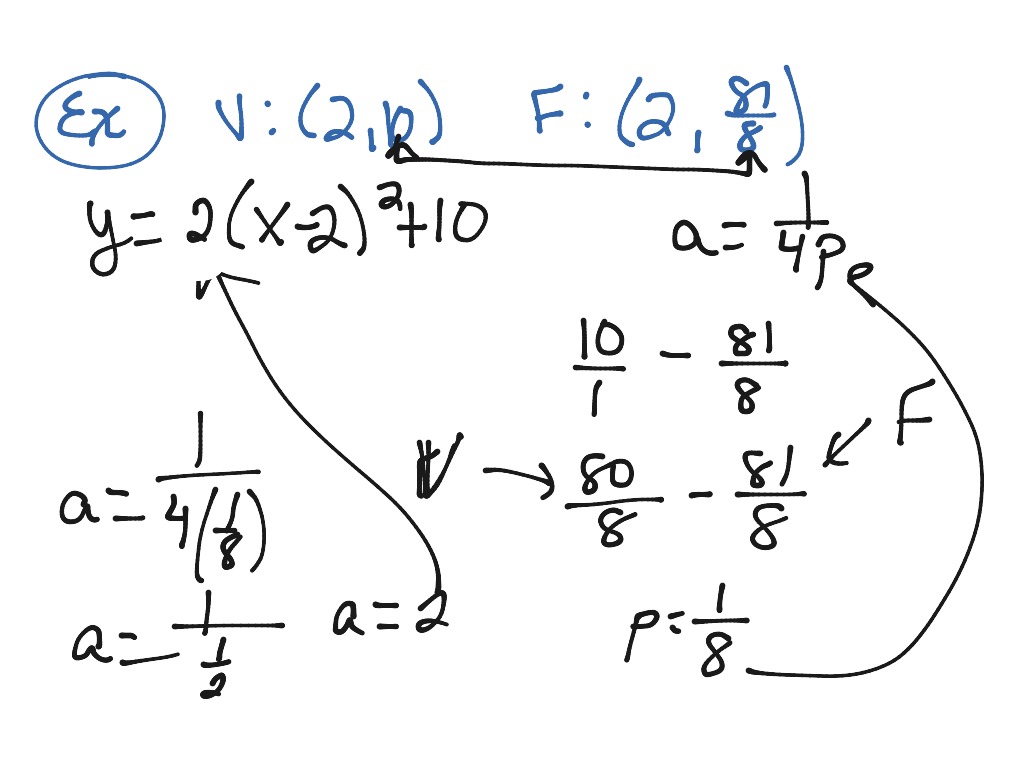
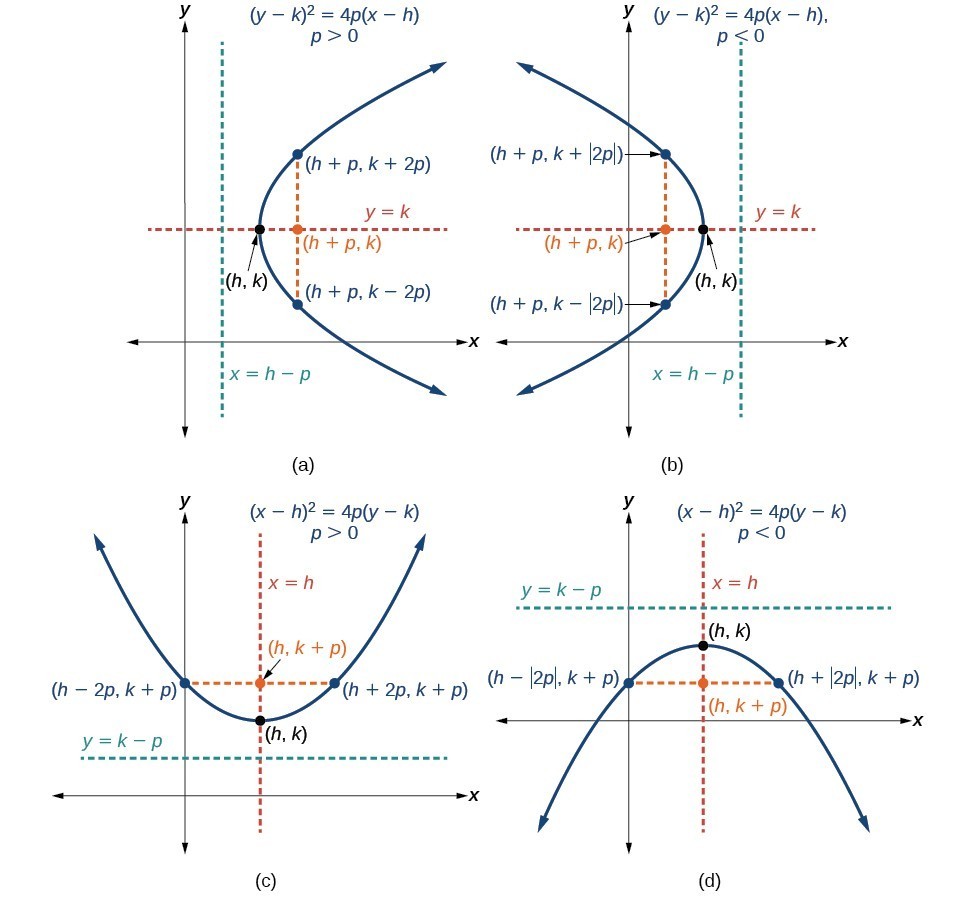
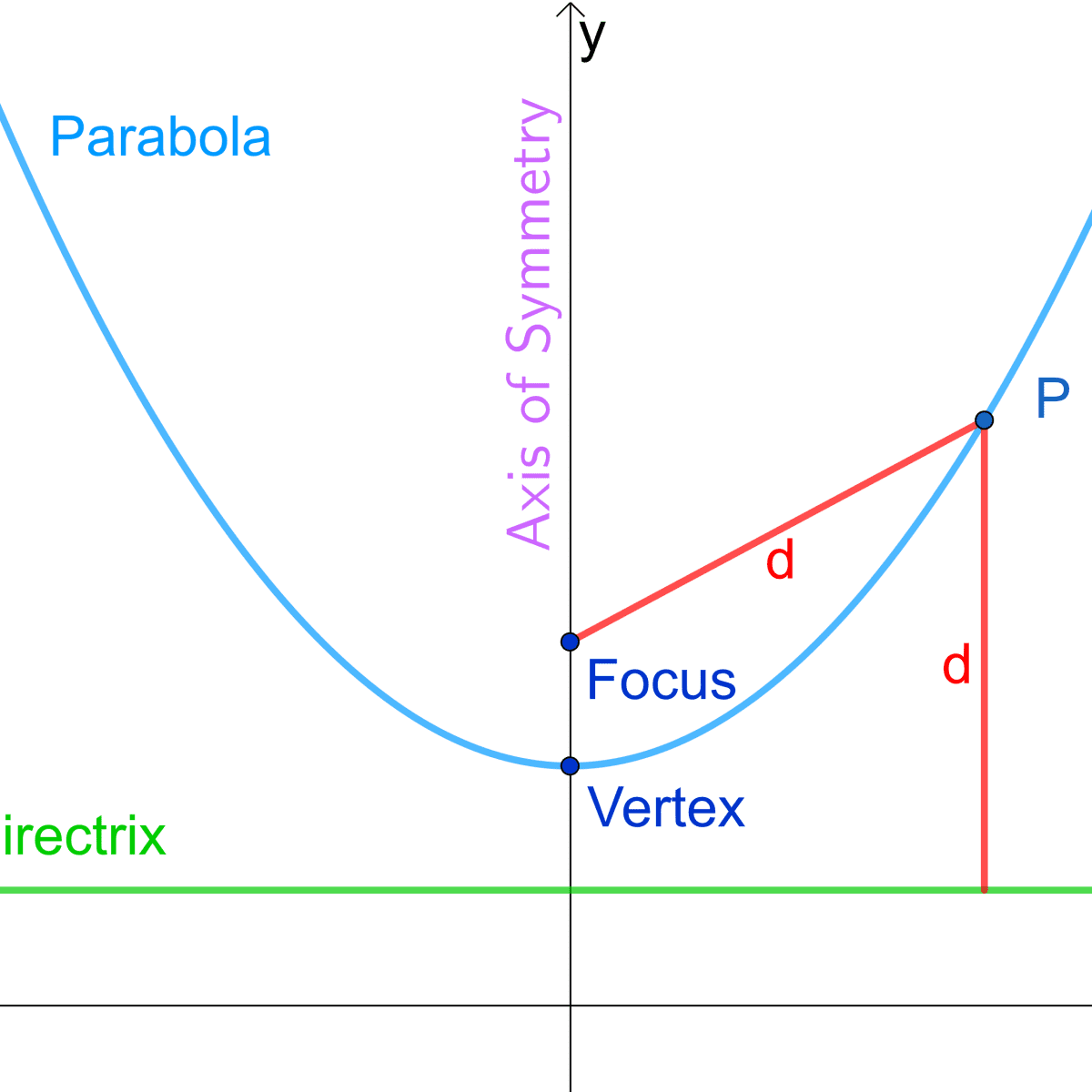
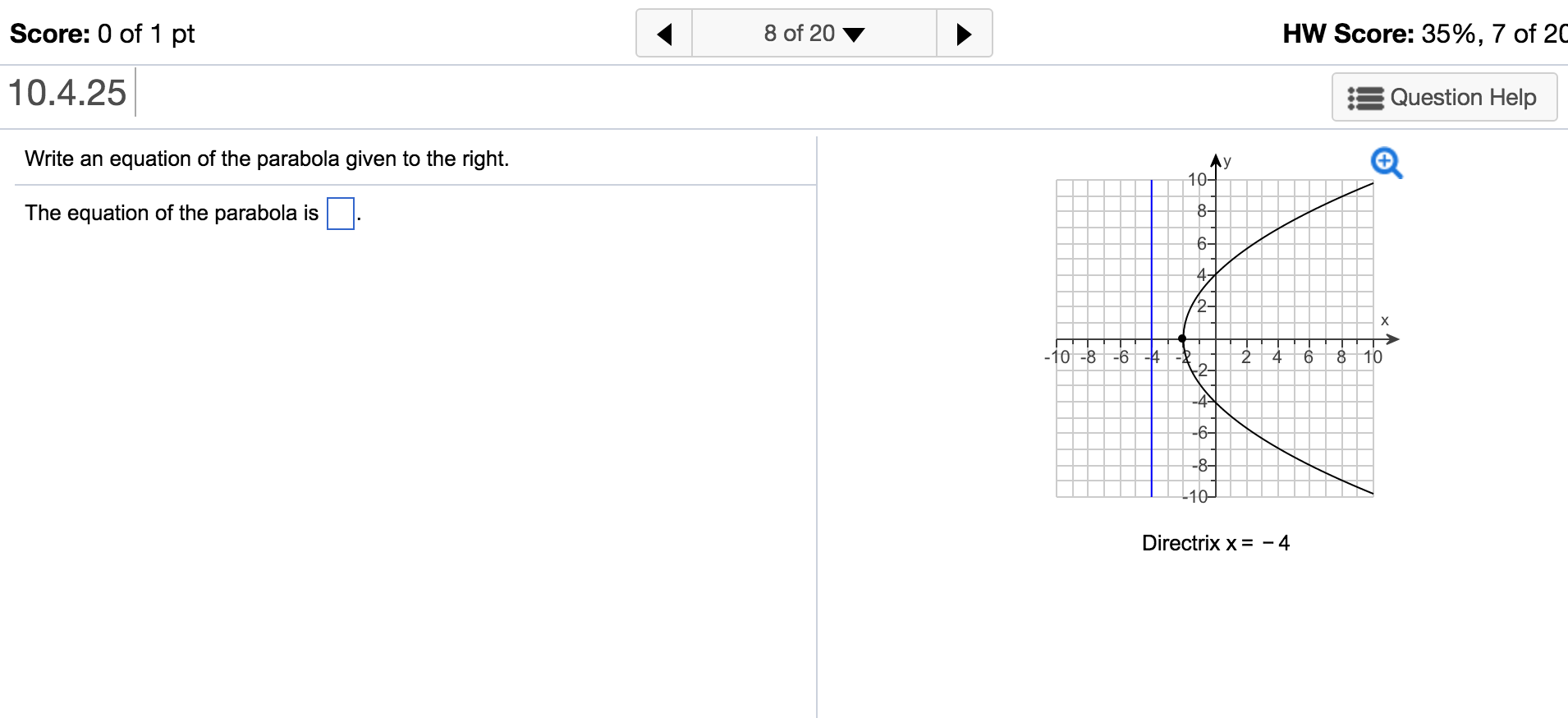
How To Write An Equation For A Parabola – How To Write An Equation For A Parabola
| Delightful to our website, in this period I will explain to you about How To Factory Reset Dell Laptop. Now, this is actually the primary photograph:

What about image above? can be which wonderful???. if you believe consequently, I’l l provide you with a number of graphic again under:
So, if you’d like to have these awesome photos about (How To Write An Equation For A Parabola), click save link to save these images for your laptop. They are available for transfer, if you like and wish to get it, click save symbol on the page, and it’ll be instantly saved to your computer.} As a final point if you would like have new and latest photo related to (How To Write An Equation For A Parabola), please follow us on google plus or save this page, we try our best to offer you regular up-date with fresh and new shots. Hope you like staying right here. For many updates and latest news about (How To Write An Equation For A Parabola) graphics, please kindly follow us on twitter, path, Instagram and google plus, or you mark this page on bookmark area, We try to give you up-date regularly with fresh and new images, love your browsing, and find the ideal for you.
Here you are at our site, contentabove (How To Write An Equation For A Parabola) published . Nowadays we are delighted to announce that we have discovered an incrediblyinteresting topicto be discussed, namely (How To Write An Equation For A Parabola) Many people searching for specifics of(How To Write An Equation For A Parabola) and definitely one of them is you, is not it?