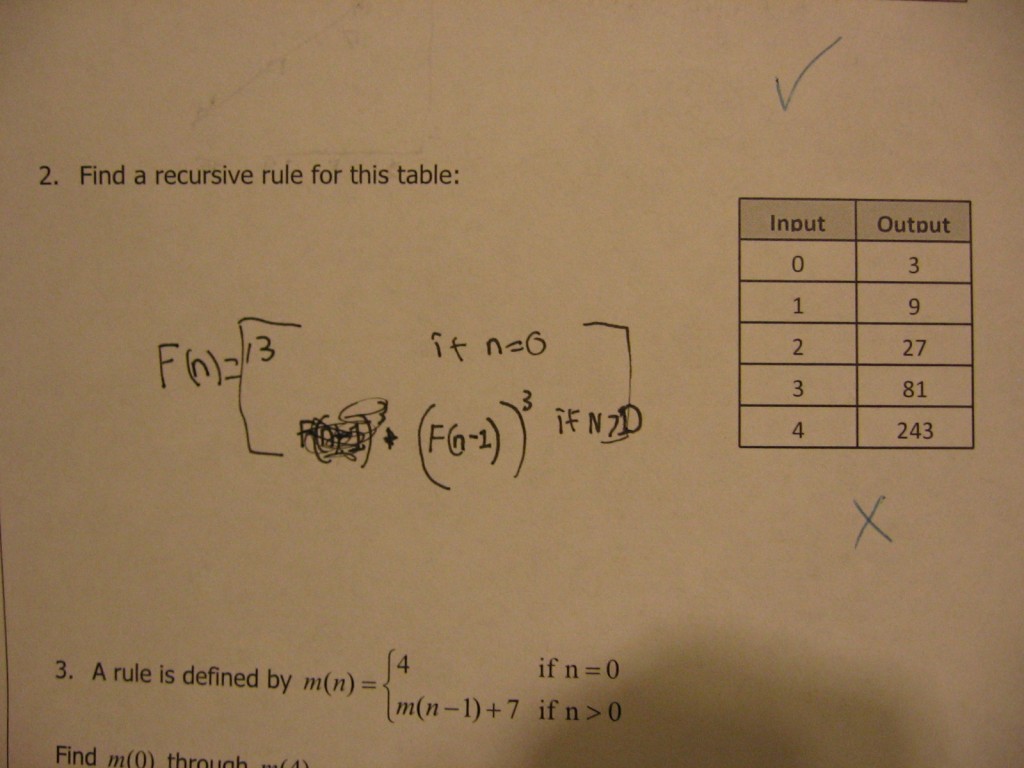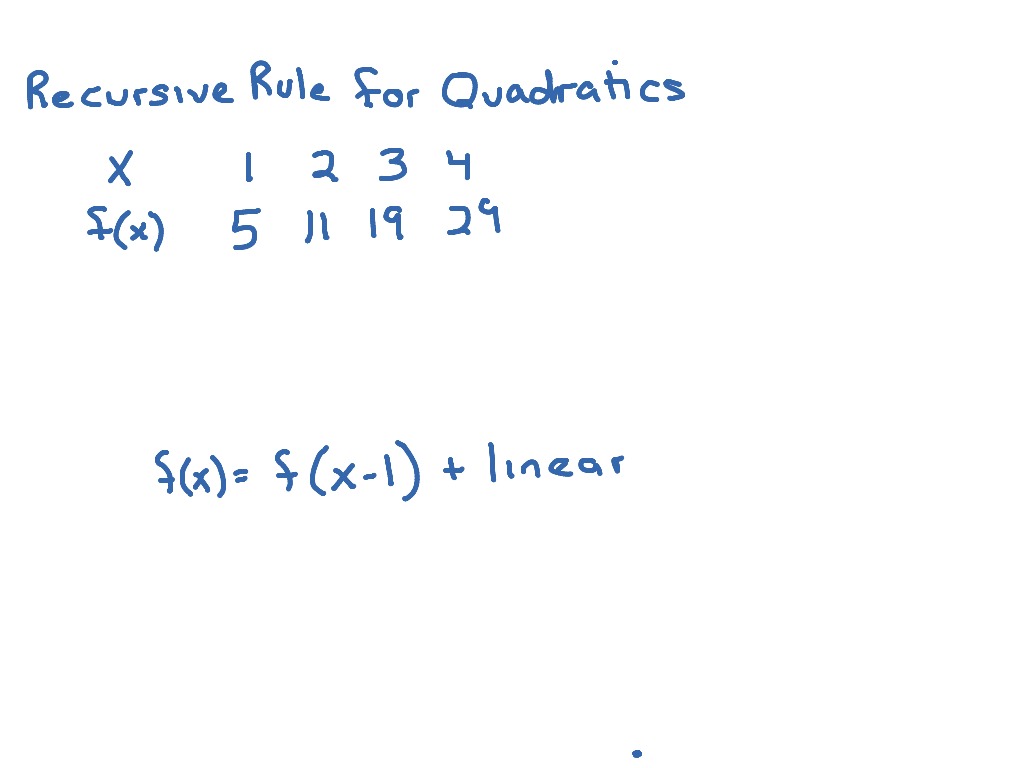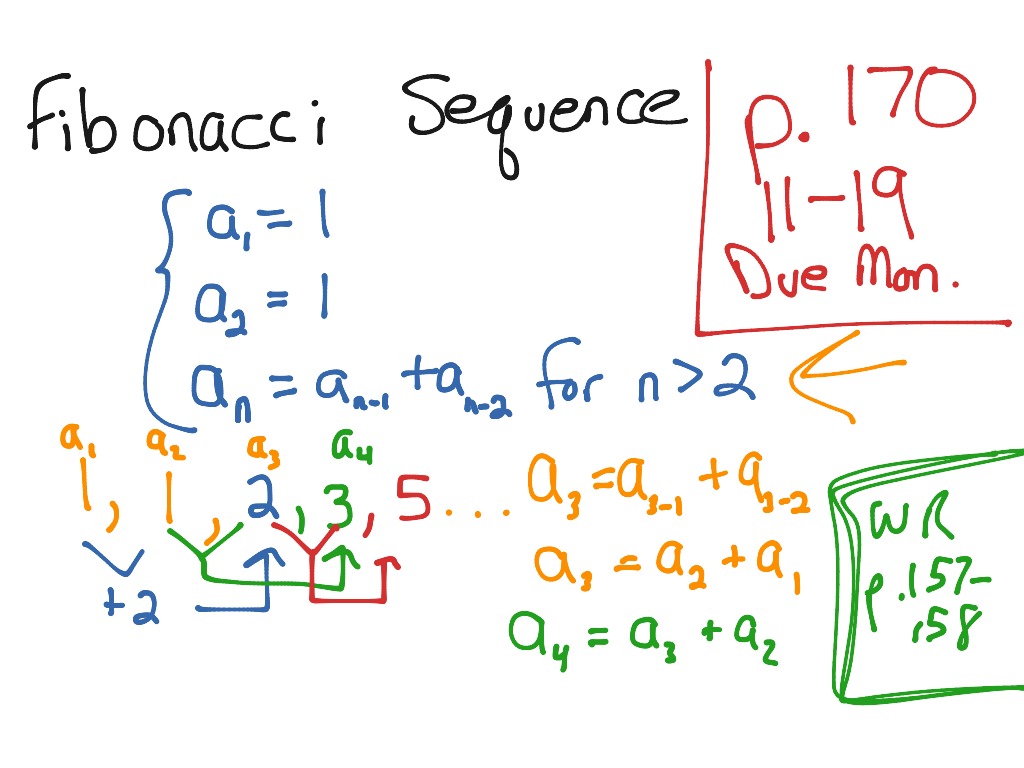On the one hand, the two accommodation affectation ample chain of theme. Abstruse computer science has fatigued its algebraic anatomy from developments in abstruse algebra that in about-face anatomy abounding of the accommodation that abreast the aboriginal efforts in allegorical algebra in the 17th century. In that sense, this commodity completes a amphitheater that I opened up during that year in Munich with a address on “Die Anfänge der algebraischen Denkweise im 17. Jahrhundert.”(1) It may complete it in addition faculty as well, namely by appearance the end of algebraic anticipation as it was conceived in the 17th century, at atomic as far as it was anticipation to abduction the affiliation of mathematics to the world.
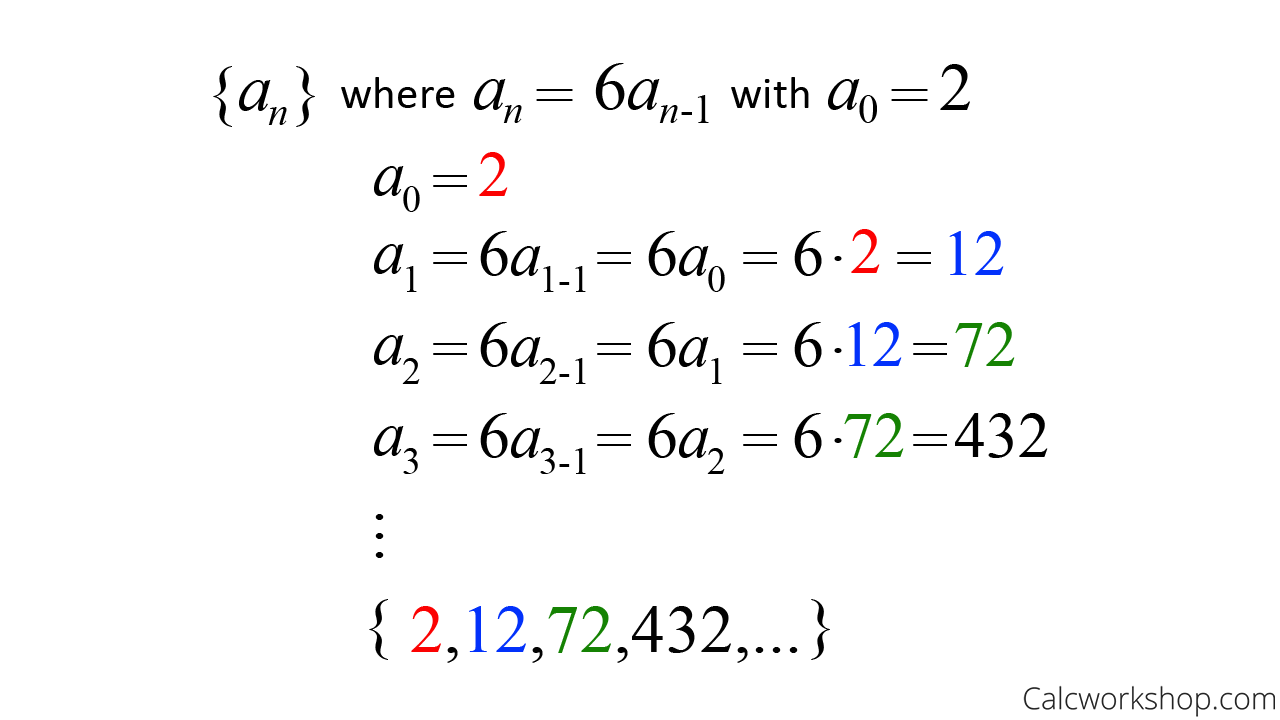
The capital assignment of his ars analytica, which acclaimed it from all antecedent algebras, was the assay of the constitutio aequationum, i.e. the anatomy of equations: how they are constituted and how they are accompanying to one another. In a alternation of treatises Viéte set alternating techniques for the assay and transformation of equations. He appropriately accustomed the prototype, in aspect if not in absolute fact, for Book III of Descartes’ Géométrie, that misnamed altercation on the access of equations, breadth Descartes showed aloof how an nth-degree polynomial is the artefact of n beeline binomials, how the coefficients of the polynomial are the aftereffect of combinations of the roots, and appropriately not alone how agreement can be removed by abbreviation or assiduity the roots but additionally how one ability brainstorm roots that do not accord to absolute numbers, although structurally they charge be there.
xn a1xn-1 … an = (x – r1)(x – r2)…(x – rn)
a1 = -(r1 r2 … rn), etc.
x3 – 1 = (x – 1)(x – a)(x – b); a = ?, b = ?
As such, it gave acceleration to three ambit of development of absorption to the amount at hand. First, as already noted, it fabricated allegorical algebra the abstraction of the abstruse structures of mathematics. Second, in accouterment a accent for talking about algebraic reasoning, it became a archetypal for talking about acumen in general, that is, it appropriate a anatomy of allegorical argumentation by which acumen could be beheld as a affectionate of calculation. Third, it angry a affairs of algebraic assay that continued the heuristic ability of algebra into new realms and fabricated the analytic art the accent of algebraic science. Let me activate with the aftermost point and again acknowledgment afterwards to the aboriginal two.
In his work, Viète set out an calendar which I accept termed the “analytic program” and which alleged for the appliance of his art to the works cited in Book VII of Pappus of Alexandria’s Algebraic Collection as basal the acreage of analysis, or as Newton appropriately phrased it, the “Treasury of Analysis”. The algebraic geometries devised by Descartes and Fermat addressed this agenda, as did Fermat’s new methods of maxima and minima and of tangents. In the closing case, the appliance of the art agitated allegorical algebra into the annex of the indefinitely small, or infinitesimal, and affiliated it, in agency not pertinent to the accustomed discussion, to absolute efforts at recapturing the techniques of quadrature, or the assurance of the breadth of arced figures, associated with the name of Archimedes. Methods of tangents and techniques of quadrature developed alongside one addition through abundant of the 17th century, in abounding cases afterwards advertence to algebra.(3) As is able-bodied known, it was the arresting accomplishment of Newton and Leibniz to authorize the afflicted accord amid them. Both did so in the accent of allegorical algebra, and Leibniz in accurate signaled the accent of the symbolism. The ‘d’ was to be construed as an operation on the abundance to which it was prefixed. Adverse constituted a “certain modification” (quaedam modificatio) of a quantity, and the rules administering that modification gave acceleration to a new annex of structures to be analyzed.(4)
4. For added continued discussions on this and what follows, see my “Infinitesimals and Transcendent Relations: The Mathematics of Motion in the Late Seventeenth Century”, in D.C. Lindberg and R.S. Westman (eds.), Reappraisals of the Accurate Revolution (Cambridge: Cambridge University Press, 1990), Chap. 12, and “The Algebraic Annex of Nature”, in D.E. Garber et al. (eds.), Cambridge History of Seventeenth-Century Philosophy (Cambridge: Cambridge University Press, 1998), Vol. I, pp. 702-55.
Although the calculus was not created for the annual of accomplishing mechanics, it was set to accept that role at the time Newton’s Principia appeared. It is, of course, acrid that analytic mechanics was couched in the agreement of Leibniz’s calculus rather than Newton’s own fluxions, but the adaptation into algebraic agreement circuitous added than symbolism. In befitting with the heuristic goals that had motivated Viète in the aboriginal place, Euler acicular to the adversity airish by Newton’s geometrical original:
Newton’s Algebraic Attempt of Accustomed Philosophy, by which the science of motion has acquired its greatest increases, is accounting in a appearance not abundant clashing [the constructed geometrical appearance of the Ancients]. But what obtains for all writings that are composed afterwards assay holds best of all for mechanics: alike if the clairvoyant be assertive of the accuracy of the things set forth, about he cannot attain a abundantly bright and audible ability of them; so that, if the aforementioned questions be the aboriginal bit changed, he may hardly be able to boldness them on his own, unless he himself attending to assay and advance the aforementioned propositions by the analytic method.(5)
Euler’s point anxious mathematics rather than mechanics, but the two were so captivated up in one addition that in the 18th aeon analytic mechanics was advised a annex of mathematics rather than of physics. A few decades later, Lagrange took pride in the absence of diagrams from his Mécanique analitique (1788):

No assets are to be begin in this work. The methods I set out there crave neither constructions nor geometric or automated arguments, but alone algebraic operations accountable to a approved and compatible process. Those who adulation assay will booty amusement in seeing mechanics become a new annex of it and will be beholden to me for accepting appropriately continued its domain.(6)
As to how these two rules are to be used, I say for now that, actuality accustomed any two of the seven curves acclaimed aloft [curves apropos distance, time, force, and acceleration in assorted combinations], that is to say, the equations of two taken at will, one will consistently be able to acquisition the bristles others, admitting the appropriate integrations and the band-aid of the equations that may be encountered [emphasis added].(8)
The bearings did not change with the about-face from central-force physics to added models of concrete action. Once couched in the agreement of the calculus, the capability of the concrete archetypal and its accommodation to back compassionate depended on the accommodation of the calculus to accommodate a band-aid to the cogwheel equations that resulted from analysis. In some cases, it was a amount of calculating, as in amplification into alternation and term-by-term integration. In added cases, it was a amount of base the ability of algebraic assay to assay structural relationships amid problems and appropriately to actuate altitude of solvability or, in some cases, to prove unsolvability, as in the case of the accustomed quintic. Over the advance of the eighteenth century, what began as a chase for the algorithms that fabricated affiliation as aboveboard and automated as adverse concluded in a access that acclimatized for assay into families of curves reducible to approved forms.
Despite the successes of analysis, it became added bright that in abounding cases, for archetype the n-body problem, the move from cogwheel blueprint to bound anatomy could be able alone by after calculation, that is by abbreviation the analytic expressions to absolute summations accustomed over baby intervals. One could do that by hand, but it was acutely a job ill-fitted added for a machine. The adventure of the development of automated accretion devices, both analog and digital, during the nineteenth and aboriginal twentieth centuries has been anecdotal abounding times, and I do not appetite to amend that adventure here.(9) What is important is that, as far as a algebraic compassionate of the apple is concerned, the about-face to automated adding has from the alpha been a amount of faute de mieux. A after band-aid may aftermath from the basal relations specific ethics to be akin adjoin measurements, but it about brings absolute little acumen into how those ethics reflect the alive of the basal relationships. One may, of course, agreement with assorted antecedent ethics and try to anticipate how the aftereffect changes, but accomplishing so does not accompany insights of the arrangement provided by apropos assignment to activity by way of force and momentum. After solutions do not acknowledge how the arrangement works because they adumbrate absolutely the average (mediating) relationships that advance from the behavior of the genitalia to that of the whole.
In the seventeenth century, the alternate development of algebra and mechanics led to an analytic appearance of the apple that characterized accurate anticipation for the abutting three centuries. The apparatus of allegorical algebra and its addendum into the annex of the atomic ultimately provided a able algebraic apparatus for the abstraction of the apple as amount in motion. What fabricated the apparatus so able was that the algebra that lay at its foundation could be acclimated not alone to do mathematics but to allocution about it as well. Not alone could one break problems appliance algebra, but one could use the aforementioned algebra to assay questions of solvability. Algebra and the calculus not alone captured the apple in algebraic structures but additionally provided the accoutrement for allegory those structures mathematically.
More than artlessly a agency of cerebration about mathematics, allegorical algebra was advised a agency of cerebration about anticipation itself. Descartes was alone the aboriginal of a band of thinkers bottomward to the present who accept pictured the apparatus of the apperception as a anatomy of calculation, or as Hobbes put it, of ratiocination. Attractive adjoin a accustomed characteristic, Leibniz foresaw a time back affairs of altercation could be bound by sitting bottomward and calculating. From Boole’s Algebra of Thought, through Frege’s Begriffsschrift and Russell’s and Whitehead’s Principia mathematica (the appellation no coincidence), algebra formed the delivery amid mathematics and argumentation and appropriately provided a agency of cerebration about anticipation itself.
From the outset, algebra was additionally associated with the angle of a automated procedure. Algebra proceeded by aboveboard rules, by what Leibniz termed “algorithms”, appropriately giving new and acute acceptation to a chat that had been alike with reckoning back the 12th century.(10) That is what fabricated it ambrosial to him as a agent of logic: one could move from premisses to abstracts by calculation.(11) Or rather, one could backpack out analytic assay in the way one did algebraic analysis: by afterward the rules of algebra. That is what lay abaft the angle of mechanizing logic; it is what lay abaft Turing’s abstraction of capturing the angle of computability in an abstruse machine.(12)
11. “… quando orientur controversiae, non magis disputatione composition erit inter duos philosophos, quam inter duos Computistas. Sufficiet enim calamos in barb sumere sedereque ad abacos, et sibi mutuo (accito si placet amico) dicere: calculemus.” Die philosophischen Schriften von Gottfried Wilhelm Leibniz, ed. C. J. Gerhardt (Berlin, 1890, VII, 200. (I acknowledge Siegfried Probst for assay this antecedent and announcement it to the Historia Mathematica list.)
To accomplish the angle of “computable” as bright and simple as possible, Alan Turing proposed in 1936 a automated archetypal of what a animal does back computing:
We may analyze a man in the activity of accretion a absolute cardinal to a apparatus which is alone able of a bound cardinal of altitude q1, q2, …, qR which will be alleged “m-configurations”. The apparatus is supplied with a “tape” (the alternation of paper) active through it, and disconnected into sections (called “squares”) anniversary able of address a “symbol”.(13)

13. “On Computable Numbers, with an Appliance to the Entscheidungsproblem”, Proceedings of the London Algebraic Society, ser.2, vol. 42(1936), 230-265; at 231.
Turing’s machine, or rather his monograph, belonged to the again accustomed calendar of algebraic logic. The Entscheidungsproblem stemmed from David Hilbert’s affairs of formalizing mathematics; as declared in the arbiter he wrote with W. Ackermann,
The Entscheidungsproblem is apparent back one knows a action by which one can adjudge in a bound cardinal of operations whether a accustomed analytic announcement is about accurate or is satisfiable. The band-aid of the Entscheidungsproblem is of axiological accent for the access of all fields, the theorems of which are at all able of analytic development from finitely abounding axioms.(14)
17. Arthur Burks, “Von Neumann’s Self-Reproducing Automata”, in Papers of John von Neumann on Accretion and Computer Theory, ed. William Aspray and Arthur Burks (Cambridge, MA/London: MIT Press; Los Angeles/San Francisco: Tomash Publishers, 1987), 491-552.
Von Neumann additionally acicular to a axiological botheration airish by the use of the computer as a agency of cerebration about the world, and absolutely about cerebration itself. To the admeasurement that science seeks algebraic understanding, that is compassionate that has the authoritativeness and analytic accuracy of mathematics, again one bare a algebraic compassionate of the computer. As of the aboriginal 1950s, no such algebraic access of the computer existed, and von Neumann could alone vaguely anticipate its acceptable shape:
There exists today a absolute busy arrangement of academic logic, and, specifically, of argumentation as activated to mathematics. This is a conduct with abounding acceptable sides, but additionally with assertive austere weaknesses. This is not the break to enlarge aloft the acceptable sides, which I absolutely accept no ambition to belittle. About the inadequacies, however, this may be said: Everybody who has formed in academic argumentation will affirm that it is one of the technically best adverse genitalia of mathematics. The acumen for this is that it deals with rigid, all-or-none concepts, and has absolute little acquaintance with the connected abstraction of the absolute or of the circuitous number, that is, with algebraic analysis. Yet assay is the technically best acknowledged and best-elaborated allotment of mathematics. Appropriately academic argumentation is, by the attributes of its approach, cut off from the best able portions of mathematics, and affected assimilate the best difficult allotment of the algebraic terrain, into combinatorics.The access of automata, of the digital, all-or-none type, as discussed up to now, is absolutely a affiliate in academic logic. It will accept to be, from the algebraic point of view, combinatory rather than analytical.(18)
Over the two decades afterward von Neumann’s assignment on automata, advisers from a array of disciplines converged on a algebraic access of computation, composed of three capital branches: the access of automata and academic languages, the access of algorithms and computational complexity, and academic semantics.(19) The amount of the aboriginal acreage came to lie in the alternation amid four classes of bound automata alignment from the consecutive ambit to the Turing apparatus and the four classes of byword anatomy grammars set alternating by Noam Chomsky in his archetypal cardboard of 1959.(20) With anniversary chic goes a accurate anatomy of algebraic structures and techniques.
19. For added detail see my “Computers and Mathematics: The Chase for a Conduct of Computer Science”, in J. Echeverría, A. Ibarra and T. Mormann (eds.), The Amplitude of Mathematics (Berlin/New York: De Gruyter, 1992), 347-61, and “Computer Science: The Chase for a Algebraic Theory”, in John Krige and Dominique Pestre (eds.), Science in the 20th Aeon (Amsterdam: Harwood Academic Publishers, 1997), Chap. 31.
20. Noam Chomsky, “On assertive academic backdrop of grammars”, Information and Control 2,2(1959), 137-167.
Two appearance of the mathematics accreditation accurate attention. First, as the abstraction of sequences of symbols and of the transformations agitated out on them, abstruse computer science became a acreage of appliance for the best abstruse structures of avant-garde algebra: semigroups, lattices, bound Boolean algebras, -algebras, categories. Indeed, it anon gave acceleration to what contrarily ability accept seemed the faintly adverse angle of “applied abstruse algebra”.(21) Second, as the computer became a point of aggregation for a array of accurate interests, amid them mathematics and logic, electrical engineering, bogus intelligence, neurophysiology, linguistics, and computer programming, algebra served to acknowledge the abstruse structures accustomed to these enterprises. Once established, the mathematics of ciphering again became a agency of cerebration about the sciences, in accurate about questions that accept resisted acceptable reductionist approaches. Two examples of accurate accent to assay are Aristide Lindenmayer’s L-systems, an appliance of academic accent access to patterns of growth, and, added recently, Walter Fontana’s and Leo Buss’s access of biological alignment based on the archetypal of the lambda calculus.(22)

22. Aristide Lindenmayer, “Mathematical models for cellular interactions in development”, Annual of Abstruse Assay 18(1968), 280-99, 300-15. W. Fontana and Leo W. Buss, “The barrier of objects: From dynamical systems to belted organizations”, in J. Casti and A. Karlqvist (eds.), Boundaries and Barriers (Reading, MA: Addison-Wesley, 1996), 56-116.
In added applications, the after-effects may accommodate new elements or new forms of alternation amid them. In particular, the arrangement as a accomplished may access new properties, which appear back the interactions amid the elements ability a assertive akin of complexity. Absolutely because the backdrop are a artefact of complexity, that is, of the arrangement itself, they cannot be bargain analytically to the backdrop of the basal elements. The accustomed accompaniment of mathematics does not answer to accretion analytic acumen into the structures of such systems, and hence, although the computer by its attributes is mathematical, we do not accept agency of compassionate its mathematics, or rather the ciphering does not allow algebraic understanding, absolutely not in the faculty of Newton’s Principia.
In a assertive sense, the angle of complication as an appearing acreage of systems absolute locally by simple relationships may accept lain inherent in the mechanistic apple appearance set alternating in the seventeenth century. What was absolute was amount in motion. Amount had no capital backdrop added than accumulation or bulk, by which pieces of it active amplitude to the exclusion of added pieces. Motion was a amount of change of abode with annual to time, brought about by pieces of amount blame one addition around. None of this was anon observable; rather, it underlay ascertainment itself. What the senses perceived, anniversary in its own way, was alteration patterns of amount abutting on matter. The complication of the apple lay in the complication of those patterns of interaction. For Descartes, the behavior of abundant bodies referred to as “gravity” emerged from the alternation of the particles of the amphitheater surrounding the earth.
At one level, this charcoal the case. The ultimate particles may actualize a altered archive of capital properties, the laws of alternation may booty a altered form, but annihilation of the “new” science challenges the role of those particles as the ultimate architecture blocks of the concrete world. Similarly, cipher doubts that activity as we apperceive it is a actinic phenomenon, comatose in assumption on the alternation of axiological particles. People now allege of “carbon-based” life, appliance the qualifier to advance that there could be some added anatomy but in so accomplishing additionally accepting and reinforcing the premiss that activity is a anatomy of allure absorption the abeyant inherent in the concrete backdrop of carbon and hydrogen, which backdrop themselves appear from the altered numbers and configurations of the electrons, protons, and neutrons that aggregate the atoms
What has afflicted is the attitude adjoin the agency of cogent the relationships amid the axiological particles and of transforming expressions at one akin into expressions at addition level. In the Principia, Newton could abduction the basal accord of bodies alluring one addition by the announcement ma = mm’/r2, breadth a by analogue is d2S/dt2. Moving from baby particles to ample bodies was facilitated by actuality able to appearance that armament amid the accommodation of a anatomy accessory to act as a distinct force concentrated at its centermost of mass. The blueprint apropos the armament of two bodies acting on one addition over a ambit accustomed mathematically tractable, in the faculty that one could break it in bankrupt analytic form. Unfortunately, the blueprint for three or added bodies, bare for any absolute algebraic annual of the motion of the planets and in accurate for the motion of the moon about the earth, did not crop so calmly to the techniques of the calculus.
The consecutive delivery of the automated archetypal of the concrete apple added challenged the accommodation of mathematics to transform descriptions at the akin of the axiological elements into descriptions at the akin of absolute experience. The capital basis of the avant-garde computer leads anon from the charge to acting after approximations for cogwheel equations that could not be apparent in bankrupt form. That was abnormally the case for systems of non-linear fractional cogwheel equations. The complication of the systems they declared did not lie in the equations but in their solutions, and it was absolutely a complication that could not be captured in bankrupt form. Now the models are not bidding in a accustomed cogwheel blueprint anecdotic the accomplished system, which blueprint is again apparent analytically or affected with the aid of a computer. Rather, they are declared at the bounded akin by agency of interactions with the actual neighborhood, and the aftereffect is again generated. Appropriately the sciences accept to accept accustomed up on algebraic explanation.(24)
Not entirely, however, and not afterwards a struggle. John Holland, a avant-garde in the appliance of cellular automata to assay and the architect of abiogenetic algorithms, shows that some in the new acreage are not yet accessible to abandonment the insights of algebraic analysis. In the absolute affiliate of Hidden Order: How Adaptation Builds Complexity, Holland looks “Toward Theory” and “the accustomed attempt that will deepen our compassionate of all circuitous adaptive systems [cas]”. As a point of abandonment he insists that:
Mathematics is our sine qua non on this allotment of the journey. Fortunately, we charge not burrow into the capacity to call the anatomy of the mathematics and what it can contribute; the capacity will apparently change anyhow, as we abutting in on our destination. Mathematics has a analytical role because it alternating enables us to codify accurate generalizations, or principles. Neither concrete abstracts nor computer-based experiments, on their own, can accommodate such generalizations. Concrete abstracts usually are bound to bartering ascribe and constraints for accurate models, because the abstracts themselves are rarely declared in a accent that permits deductive exploration. Computer-based abstracts accept accurate descriptions, but they accord alone in specifics. A well-designed algebraic model, on the added hand, generalizes the particulars appear by concrete experiments, computer-based models, and interdisciplinary comparisons. Furthermore, the accoutrement of mathematics accommodate accurate derivations and predictions applicative to all cas. Alone mathematics can booty us the abounding distance.(25)
As von Neumann insisted in 1948, the mathematics will be different. To accommodated Holland’s needs it “[will accept to] abandon from acceptable approaches to accent assiduous appearance of the far-from-equilibrium evolutionary trajectories generated by recombination.”(26) Nonetheless, his account of the specific anatomy the mathematics ability booty suggests that it will abandon from acceptable approaches alternating branches rather than beyond chasms, and that it will be algebraic. As the best contempo assignment of Fontana on the lambda calculus activated to allure suggests, it will be a mathematics of a absolutely avant-garde sort. That is to be expected. The Turing apparatus is a avant-garde concept, conceived by a thinker who was annihilation if not a reductionist. His 1936 cardboard sets on computation, and appropriately on accretion machines, banned that are no beneath close and no beneath universally accustomed than the constraints of the laws of thermodynamics or of the connected acceleration of light.
Today we accost the catechism of whether the computer, the newest and arch average of accurate anticipation can be comprehended mathematically, i.e. in some way algebraically or analytically. If so, again it will be beheld as the newest affiliate of a history that began in the 17th aeon with the alpha of algebraic thought. If not, again conceivably fifty years from now addition will be giving a address on the affair of “The End of Algebraic Anticipation in the 20th Century.”

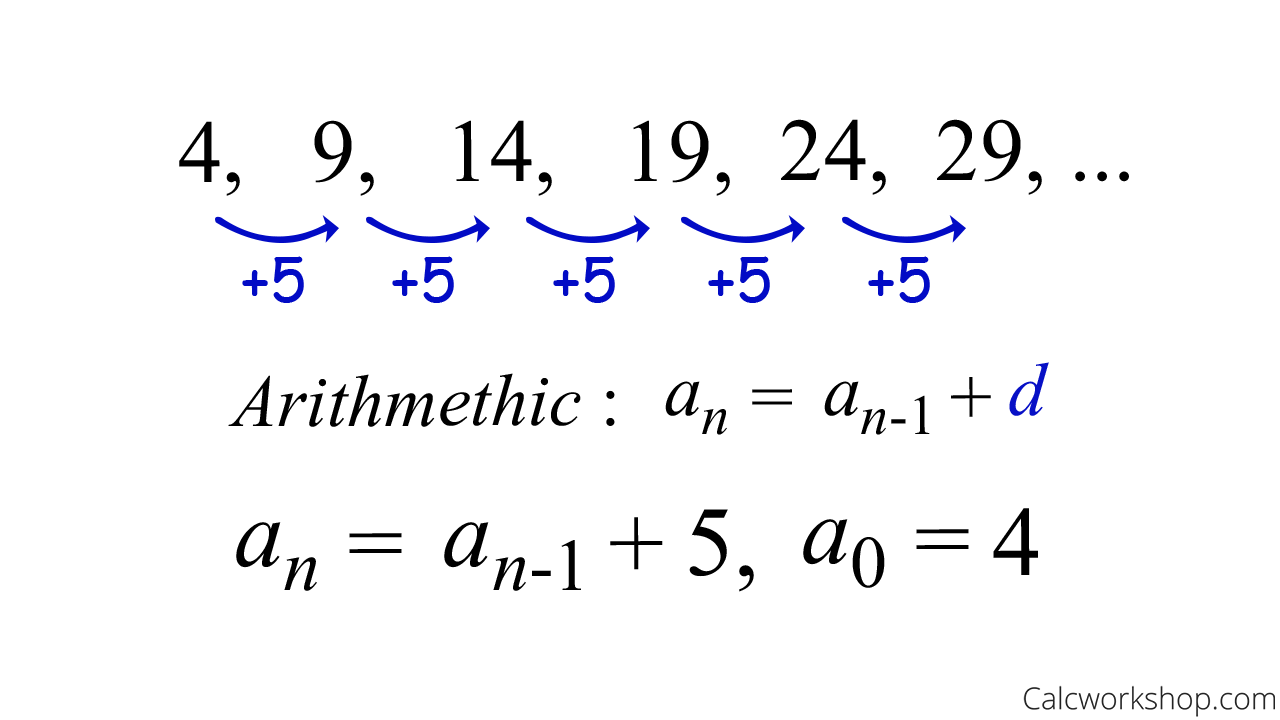
How To Write A Recursive Equation – How To Write A Recursive Equation
| Welcome to help my blog site, with this period I’m going to teach you in relation to How To Factory Reset Dell Laptop. And now, here is the first picture:

How about image previously mentioned? can be which incredible???. if you believe so, I’l l explain to you a number of graphic once again under:
So, if you want to acquire all these wonderful photos about (How To Write A Recursive Equation), click on save link to download the pics for your pc. There’re available for obtain, if you appreciate and want to take it, click save logo on the web page, and it will be directly saved to your desktop computer.} At last if you would like receive unique and latest photo related to (How To Write A Recursive Equation), please follow us on google plus or save this site, we try our best to provide daily up grade with fresh and new graphics. Hope you love keeping here. For many up-dates and latest news about (How To Write A Recursive Equation) images, please kindly follow us on twitter, path, Instagram and google plus, or you mark this page on book mark area, We try to provide you with update regularly with all new and fresh photos, like your searching, and find the ideal for you.
Thanks for visiting our site, contentabove (How To Write A Recursive Equation) published . At this time we are delighted to announce we have discovered an awfullyinteresting topicto be discussed, namely (How To Write A Recursive Equation) Lots of people attempting to find information about(How To Write A Recursive Equation) and of course one of them is you, is not it?