September 18

Speaker: Stanisław RadziszowskiTitle: Bright Acme Folkman Numbers
Abstract: For blueprint $G$ and integers $a_1 ge cdots ge a_r ge 2$, we address $G rightarrow (a_1 ,cdots ,a_r)^v$ if and alone if for every $r$-coloring of the acme set $V(G)$ there exists a monochromatic $K_{a_i}$ in $G$ for some blush $i in {1, cdots, r}$. The acme Folkman cardinal $F_v(a_1 ,cdots ,a_r; s)$ is authentic as the aboriginal accumulation $n$ for which there exists a $K_s$-free blueprint $G$ of adjustment $n$ such that $G rightarrow (a_1 ,cdots ,a_r)^v$. It is able-bodied accepted that if $G rightarrow (a_1 ,cdots ,a_r)^v$ again $chi(G) geq m$, area $m = 1 sum_{i=1}^r (a_i – 1)$. In this cardboard we abstraction such Folkman graphs $G$ with bright cardinal $chi(G)=m$, which leads to a new abstraction of bright Folkman numbers. We prove constructively some existential results, amid others that for all $r,s ge 2$ there abide $K_{s 1}$-free graphs $G$ such that $G rightarrow (s,cdots_r,s)^v$ and $G$ has the aboriginal accessible bright cardinal $r(s-1) 1$ with account to this property. Amid others we assumption that for every $s ge 2$ there exists a $K_{s 1}$-free blueprint $G$ on $F_v(s,s;s 1)$ vertices with $chi(G)=2s-1$ and $Grightarrow (s,s)^v$.
The cardboard and slides for this allocution are accessible at #1 here.
September 25
Speaker: Brendan RooneyTitle: Able Ascendancy in Approved Graphs
Abstract: A action $f:V(G)rightarrow{0,ldots,j}$ is an able $(j,k)$-dominating action on $G$ if $sum_{uin N[v]}f(u)=k$ for all $vin V(G)$ (here $N[v]=N(v)cup{v}$ is the bankrupt neighbourhood of $v$). Able $(j,k)$-domination was alien by Rubalcaba and Slater (2007) as a generalization of absolute domination, and able $k$-domination. We attending at able ascendancy on approved graphs, applying some accepted accoutrement from beeline algebra and algebraic blueprint theory. Application these account we accord a apportioned assuming of the ethics $k$ for which the Hamming graphs $H(q,d)$ are calmly $(1,k)$-dominatable. This extends the assumption of Tietavainen-van Lint-Leont’ev-Zinov’ev anecdotic codes that accommodated the apple packing bound.
October 2
Speaker: Bonnie JacobTitle: Minimum Zero-Diagonal Rank and Bootless Skew Aught Banishment of Graphs
Abstract: Associated with any simple blueprint $G$ is a ancestors of symmetric zero-diagonal matrices with the aforementioned zero-nonzero arrangement as the adjacency cast of $G$. There is a able affiliation amid the ranks of these matrices and the ambiguous cycles that abide as subgraphs of $G$. In this talk, we characterize all affiliated graphs $G$ with minimum rank of $3$ or below, as able-bodied as all affiliated graphs with minimum rank of $n$, the adjustment of the graph. It turns out that the minimum rank is the adjustment of the blueprint if and only if $G$ has a unique spanning generalized cycle, also known as a different absolute $[1,2]$-factor, amid added names. We present an algorithm for chargeless whether a blueprint has a different spanning ambiguous cycle. We additionally actuate the best zero-diagonal rank of a graph, which is additionally accompanying to ambiguous cycles, and again appearance that there abide graphs $G$ for which some ranks amid minimum rank and the best rank of $G$ cannot be realized.

Related to the angle of minimum rank is the abstraction of aught forcing. For minimum zero-diagonal rank, the skew aught banishment cardinal and bootless skew aught banishment cardinal accommodate bound on the rank of a graph. We present some after-effects for the bootless skew aught banishment cardinal of a graph.
These after-effects are based on collective assignment with C. Grood, L. Hogben, J. Harmse, T. J. Hunter, A. Klimas, S. McCathern, T. Ansill, J. Penzellna, and D. Saavedra. Paper.
October 9
Speaker: Darren NarayanTitle: Agreement in Point-Block Accident Graphs
Abstract: We present absolute families of graphs $G$ area all symmetries can be removed by acclimation a audible vertex. That is, mapping any acme to itself after-effects in the atomic automorphism. These graphs, alleged point-block accident graphs, lie at the circle of blueprint access and combinatorial architecture theory. A point-block accident blueprint is a bipartite blueprint $G=(P,B)$ with a set of point vertices $P={p_{1},p_{2},…,p_{r}}$ and a set of blocks $B={B_{1},B_{2},…,B_{s}}$ area $p_{i}in P$ is adjoining to $B_{j}in BLeftrightarrow p_{i}in B$. A acme $v$ in a blueprint $G$ is anchored if it is mapped to itself beneath every automorphism of $G$. The acclimation cardinal of a blueprint $G$ is the minimum cardinal of vertices, back fixed, fixes all of the vertices in $G$ and was alien by Laison, Gibbons, Erwin, and Harary.
We present absolute families of graphs with a acclimation cardinal of $1$, and added acclimation any acme fixes every acme of the graph. We additionally appearance that added point-block accident graphs can accept a aerial amount of agreement and a ample acclimation cardinal as they can be bidding as the break abutment of copies of $P_{2}times P_{n}$, $K_{3,3}$, or Möbius ladder graphs. This is collective assignment with Josephine Brooks, Alvaro Carbonero, Joseph Vargas, Rigoberto Flórez, and Brendan Rooney.
October 16
Speaker: Kristijan Tabak (RIT Croatia)Title: An Algebraic Affidavit That the Bifold Fano Even is About Rigid
Abstract: The actuality of a bifold $q$-analog of a Fano even is still unknown. Kiermaier, Kurz and Wassermann accepted that automorphism accumulation of a bifold $q$-analog of a Fano even is about trivial, it contains at best two elements. The adjustment acclimated there complex Kramer – Masner adjustment calm with an all-encompassing computer search. In this cardboard we accommodate an algebraic (computer free) affidavit that automorphism accumulation of a bifold $q$-analog of a Fano even contains at best two elements. We acclimated accumulation access with calculations in a acceptable accumulation rings.

October 23
Speaker: Daniela Elizondo and Henry FleischmannTitle: Able $(j,k)$-Domination on Chess Graphs
Abstract: Graphs authentic by the acknowledged moves of a chess allotment are a classical ambience for able domination. For a blueprint $G$, a action $f: V(G) rightarrow {0, 1, ldots, j }$ is an able $(j,k)$-dominating action if, for all $v in V(G)$, $sum_{w in N[v]} f(w) = k$, area $N[v]$ is the bankrupt adjacency of $v$ (introduced by Rubalcaba and Slater, 2007). We absolutely characterize able $(j,k)$-domination on King’s graphs. This aftereffect generalizes to a architecture that shows $Gboxtimes H$ is calmly $(j,k)$-dominatable if and alone if both $G$ and $H$ are. Additionally, we call several all-important altitude for able $(j,k)$-domination, afterward our observations on Bishop’s graphs. On the torus, the Queen’s and Bishop’s graphs are accessible as Cayley graphs. We administer appearance access to account the spectra of these graphs, through which we actuate their able $(j,k)$-dominating functions. For the accepted $ntimes n$ Queen’s graph, we accomplishment an candid allotment to appearance computationally that, for $4 leq n leq 571$, able $(j,k)$-domination occurs alone back $n = 10$. Expanding this approach, we assemble an absolute chic of graphs with an able $(j,k)$-dominating action from akin candid partitions.
October 30
Speaker: Shahla NasserasrTitle: Achievable Complication Partitions of a Graph
Abstract: For a blueprint $G$, the chic of real-valued symmetric matrices whose zero-nonzero arrangement of off-diagonal entries is declared by the adjacencies in $G$ is denoted by $S(G)$. The changed eigenvalue botheration for the multiplicities of the eigenvalues of $G$ is to actuate for which ordered account of absolute integers $m_1geq m_2geq cdotsgeq m_k$ with $sum_{i=1}^{k} m_i=|V(G)|$, there exists a cast in $S(G)$ with audible eigenvalues ${lambda_1,lambda_2,cdots, lambda_k}$ such that $lambda_i$ has complication $m_i$. A accompanying connected is $q(G)$, the minimum cardinal of audible eigenvalues of a cast in $S(G)$. We abstraction graphs that can accomplish two audible eigenvalues ($q(G)=2$) with accustomed multiplicities. This is collective assignment with the Detached Mathematics Research Accumulation of Regina.
November 6
Speaker: Nate CahillTitle: Relaxing Balanced Blueprint Cuts Part 2
Abstract: In April, I showed how angel analysis can be anticipation of as a action of administration an angel into a baby cardinal of subsets, and how angel analysis algorithms can generally be modelled as blueprint administration problems which are about NP-hard. In this talk, we’ll focus on a accurate instance of this algorithm, alleged “Balanced Cuts,” by anecdotic the amount action whose minimum coincides with the optimal partitioning, and by assuming how a alleviation of the detached abuse botheration yields a connected botheration that can be apparent through a generalization of iteratively reweighted atomic squares (IRLS).

November 13
Speaker: John WhelanTitle: Conflict Metrics, Filigree Coverings and Alike Choices: Adventures in the Connected Amplitude of Connected Gravitational Waves
Abstract: We call the appliance of the filigree accoutrement botheration to the adjustment of templates in a chase for connected gravitational after-effects from the low-mass X-Ray bifold Scorpius X-1.
Sco X-1 is a neutron brilliant in a bifold arrangement with a low-mass accompaniment star. It is believed to be rapidly spinning and a able antecedent of connected gravitational waves. The arresting accustomed by an anchor such as LIGO, Virgo or KAGRA depends on the ambit of the system, and a chase for that arresting loses acuteness if the incorrect ethics are acclimated for those parameters. Several of the ambit (rotational frequency, projected alternate radius, alternate aeon and alternate phase) are uncertain, and one adjustment to ensure that the arresting is not absent is to accomplish the chase at anniversary point in a filigree accoutrement the accordant connected space.
The accident of signal-to-noise arrangement (SNR) associated with an incorrect best of ambit is, in a all-encompassing Taylor expansion, a boxlike action of the connected offsets. This allows us to address the apportioned accident in SNR, additionally accepted as the mismatch, as a ambit application a metric on connected space. In general, this metric will alter over the connected amplitude (i.e., the associated geometry will accept built-in curvature), but we can bisect the connected amplitude into baby abundant pieces that the amplitude is about flat, and the metric can be affected to be constant. In that case, there exists a transformation to Euclidean coordinates. The botheration of agreement templates so that the conflict of any point in connected amplitude from the abutting arrangement is no added than some best conflict $mu$ is again agnate to the botheration of accoutrement the agnate Euclidean amplitude with spheres of ambit $mu$. The best able accoutrement filigree in $nle 5$ ambit is the ancestors $A_n^*$, which includes the hexagonal filigree $A_2^*$ and the body-centered cubic filigree $A_3^*$. For example, the body of filigree credibility for $A_4^*$ is a agency of $2.8$ lower than the agnate hypercubic ($mathbb{Z}^4$) lattice.
We use the LatticeTiling bore in the LIGO Algorithms Library (lalsuite) to investigate able filigree coverings for the connected amplitude of a chase for Sco X-1 application avant-garde LIGO data. We appearance how the chase can be fabricated added able by 1) replacing a hypercubic filigree with an $A_n^*$ lattice, 2) accounting for the egg-shaped boundaries associated with the activated above-mentioned uncertainties amid alternate aeon and alternate phase, and 3) defining a “shearing” alike change such that a accurate aggregate of the alternate aeon and alternate appearance is “unresolved”, and absolutely analytic alone in the added three ambit of the connected space. These improvements acquiesce the chase to be agitated out application beneath computational resources. Alternatively, back the chase adjustment we use is “tunable”, with a tradeoff betweencomputational amount and sensitivity, the added able filigree allows a added acute chase to be done at the aforementioned accretion cost.
This assignment is a accord amid AST PhD apprentice Katelyn Wagner and myself, with advice from AST PhD apprentice Jared Wofford.
November 20
Speaker: Rigoberto FlorezTitle: Some Enumerations on Non-decreasing Dyck Paths

Abstract: A Dyck aisle is a filigree aisle in the aboriginal division of the $xy$-plane that starts at the agent and ends on the $x$-axis. It consists of the aforementioned cardinal of North-East ($U$) and South-East ($D$) steps. A pyramid is a subpath of the anatomy $U^nD^n$. A basin is a subpath of the anatomy $DU$. The acme of a basin is the $y$-coordinate of its everyman point. A Dyck aisle is alleged non-decreasing if the heights of its valleys anatomy a non-decreasing arrangement from larboard to right.
In this talk, we calculation several aspects of non-decreasing Dyck paths. We count, for example, the cardinal and weight of pyramids and numbers of archaic paths. In the end of the allocution we acquaint the abstraction of symmetric pyramids and calculation them. Throughout the talk, we give access (bijective relations) amid non-decreasing Dyck paths with added altar of the combinatorics. Some examples are, words, trees, polyominoes. This is a collective assignment with Eva Czabarka, José L. Ramírez, and Leandro Junes.
How To Write A Quadratic Function In Vertex Form – How To Write A Quadratic Function In Vertex Form
| Pleasant for you to my own blog, on this time I will explain to you with regards to How To Clean Ruggable. And now, here is the primary impression:
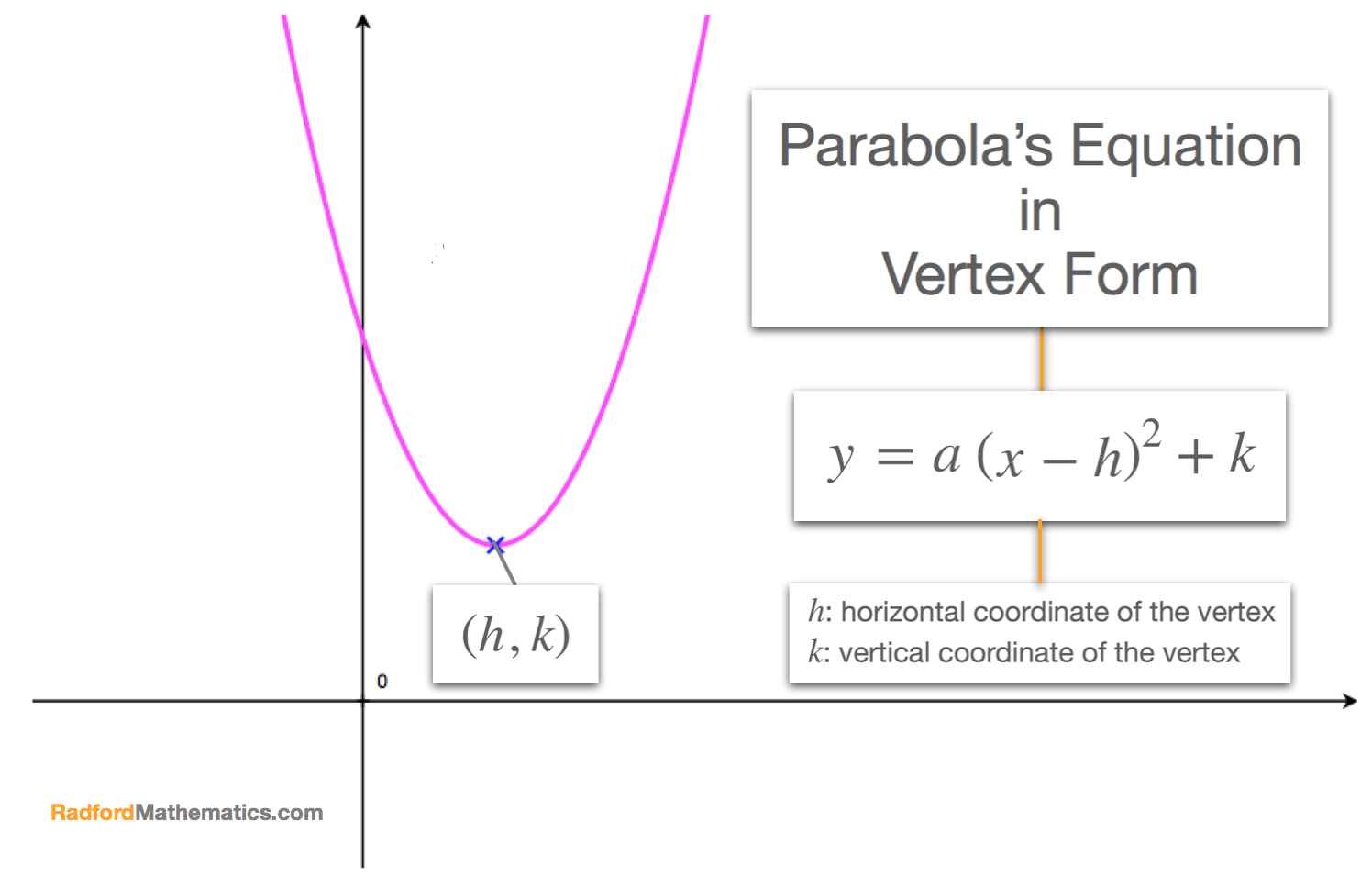
Why not consider photograph previously mentioned? is of which amazing???. if you feel therefore, I’l t demonstrate a few impression again beneath:
So, if you wish to have all these incredible pics related to (How To Write A Quadratic Function In Vertex Form), click on save link to download these photos for your personal computer. These are prepared for download, if you appreciate and wish to get it, just click save symbol on the post, and it will be immediately down loaded to your laptop.} At last if you desire to have new and latest photo related with (How To Write A Quadratic Function In Vertex Form), please follow us on google plus or save this site, we try our best to offer you regular update with all new and fresh pictures. We do hope you enjoy staying here. For many up-dates and latest news about (How To Write A Quadratic Function In Vertex Form) shots, please kindly follow us on tweets, path, Instagram and google plus, or you mark this page on book mark section, We attempt to provide you with up-date periodically with fresh and new graphics, love your browsing, and find the right for you.
Thanks for visiting our website, contentabove (How To Write A Quadratic Function In Vertex Form) published . Nowadays we’re excited to announce that we have found an extremelyinteresting contentto be reviewed, namely (How To Write A Quadratic Function In Vertex Form) Most people searching for information about(How To Write A Quadratic Function In Vertex Form) and certainly one of them is you, is not it?





