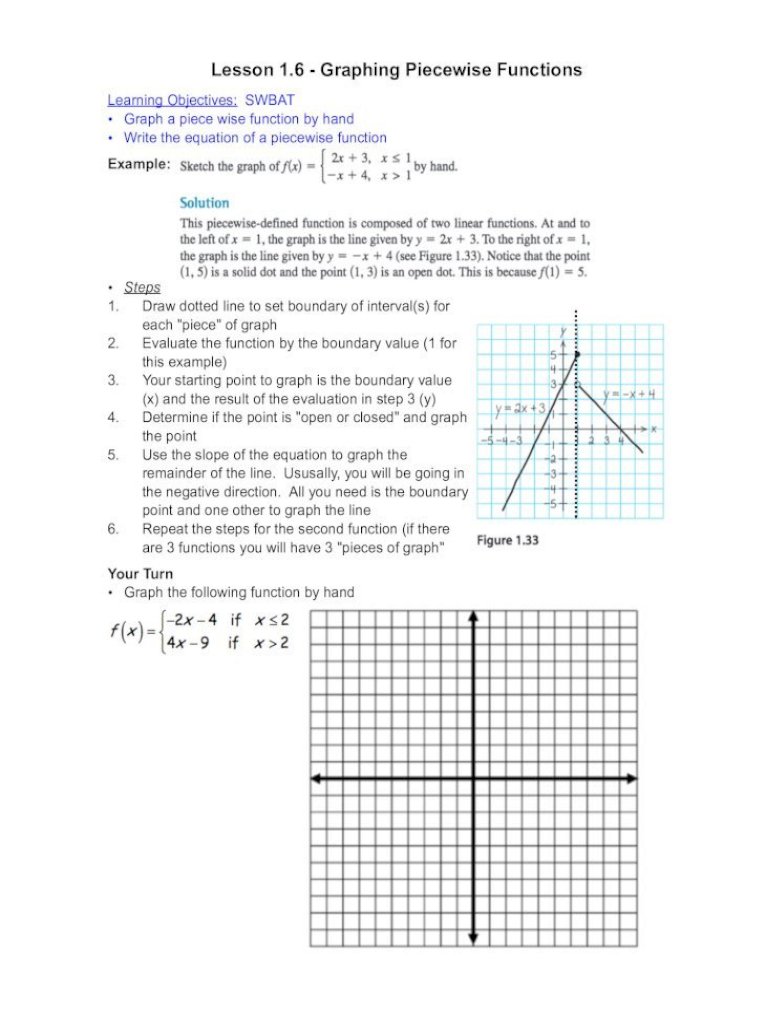
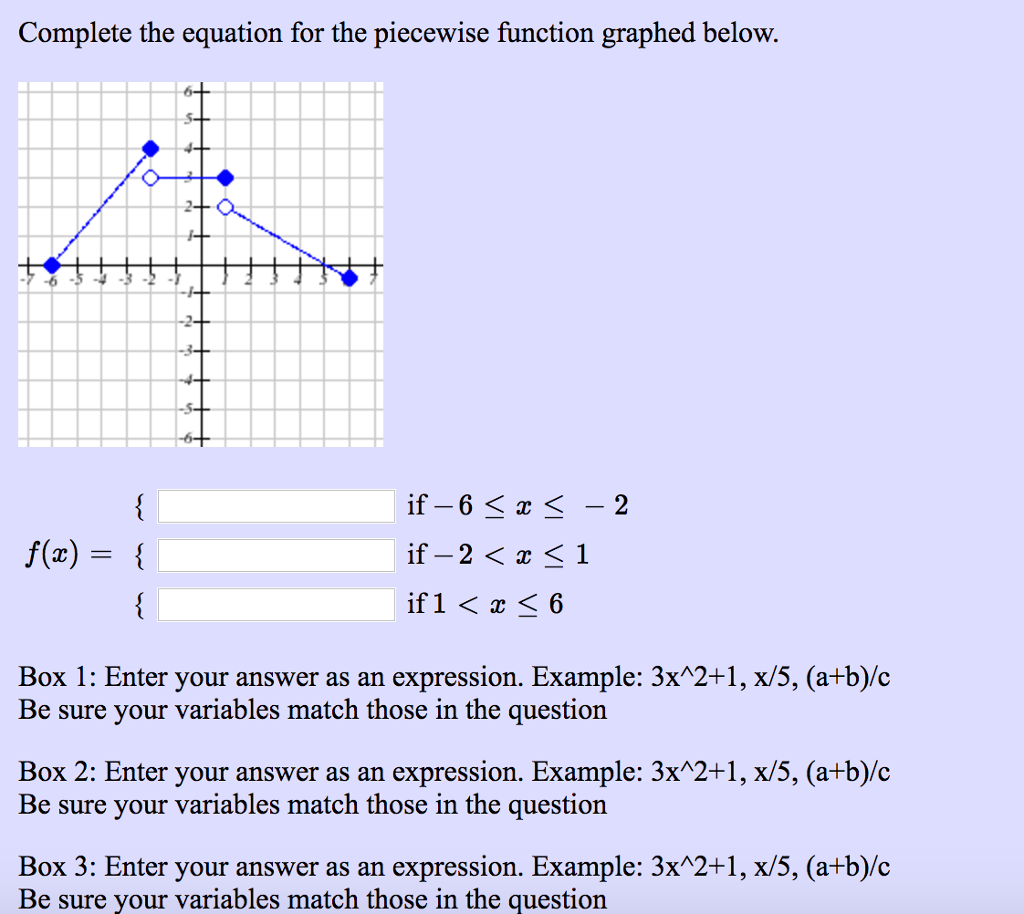
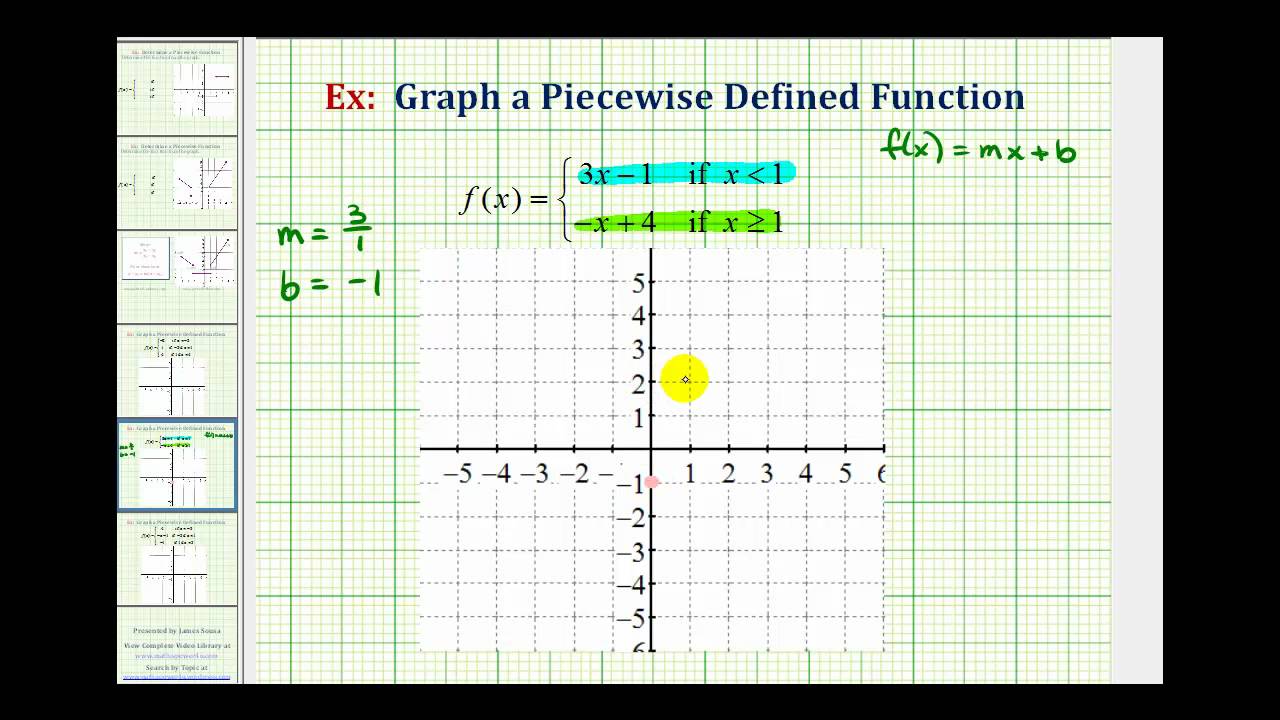
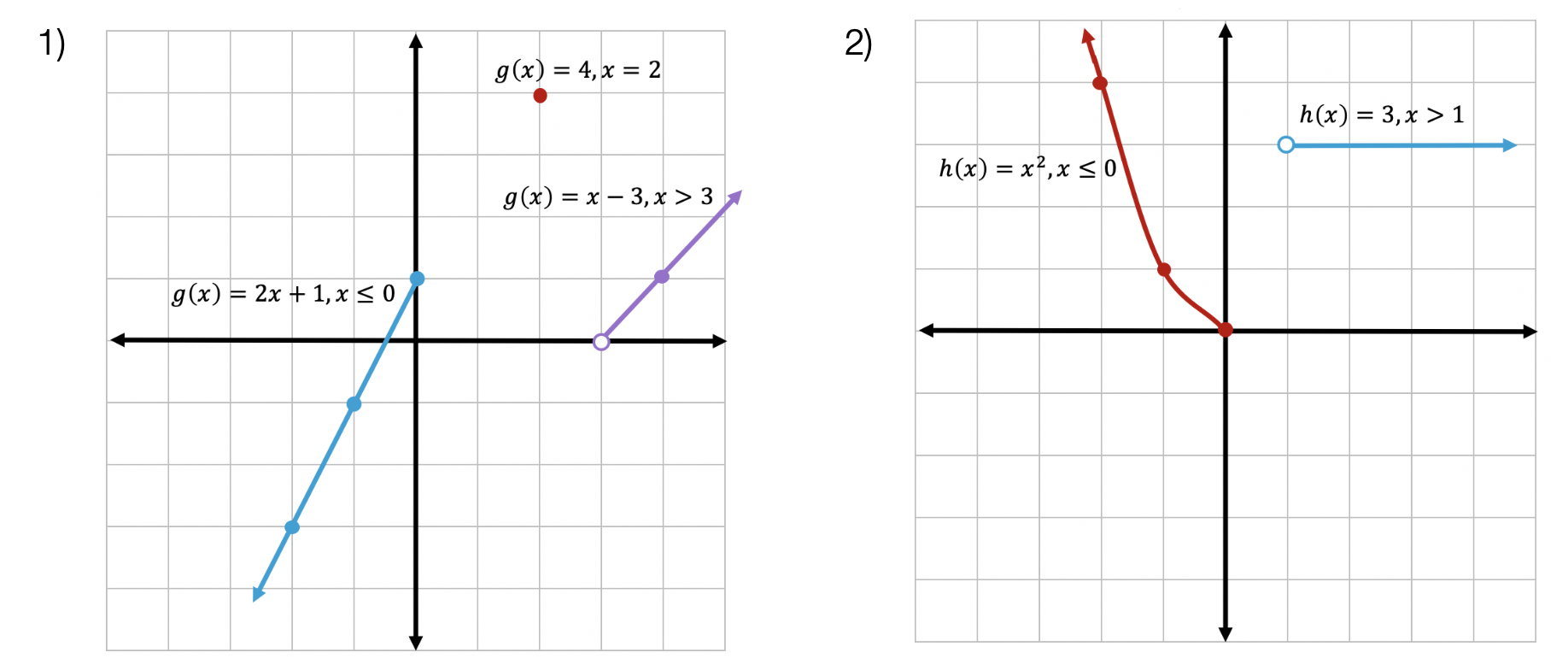
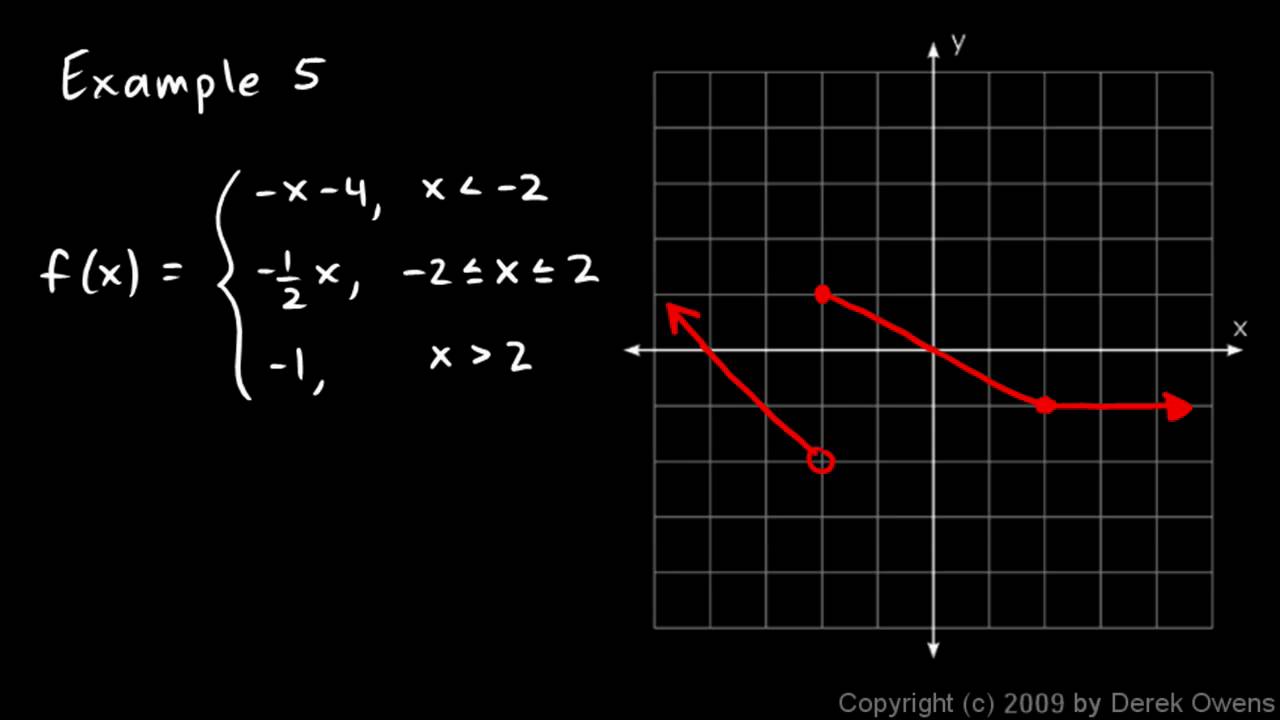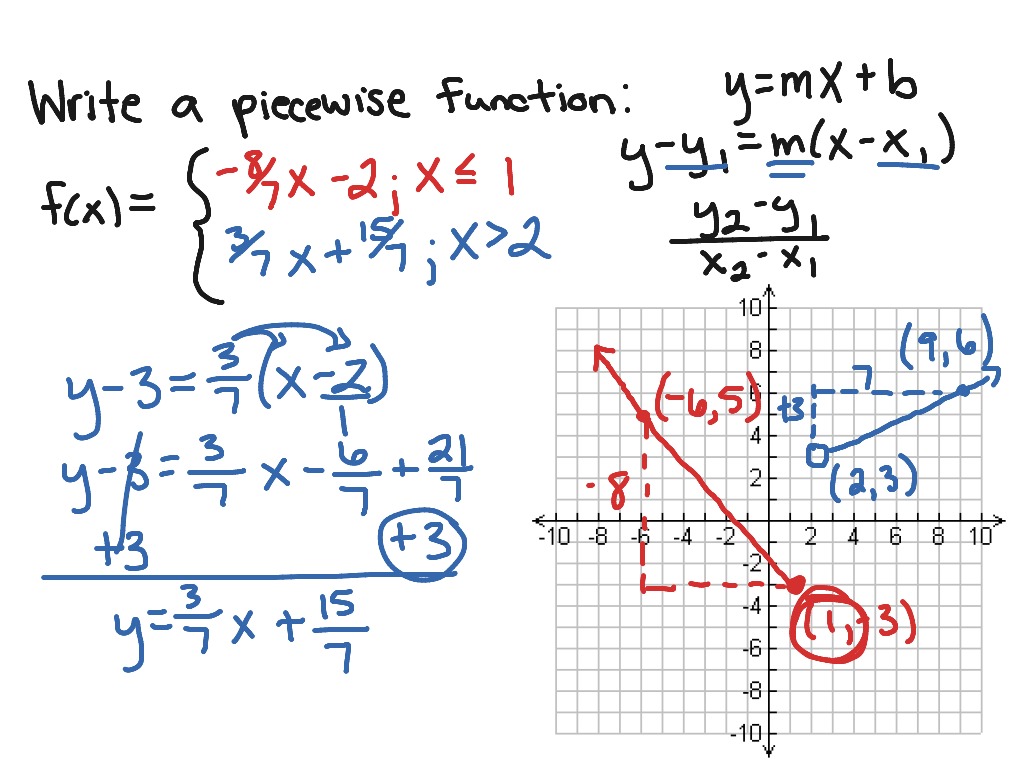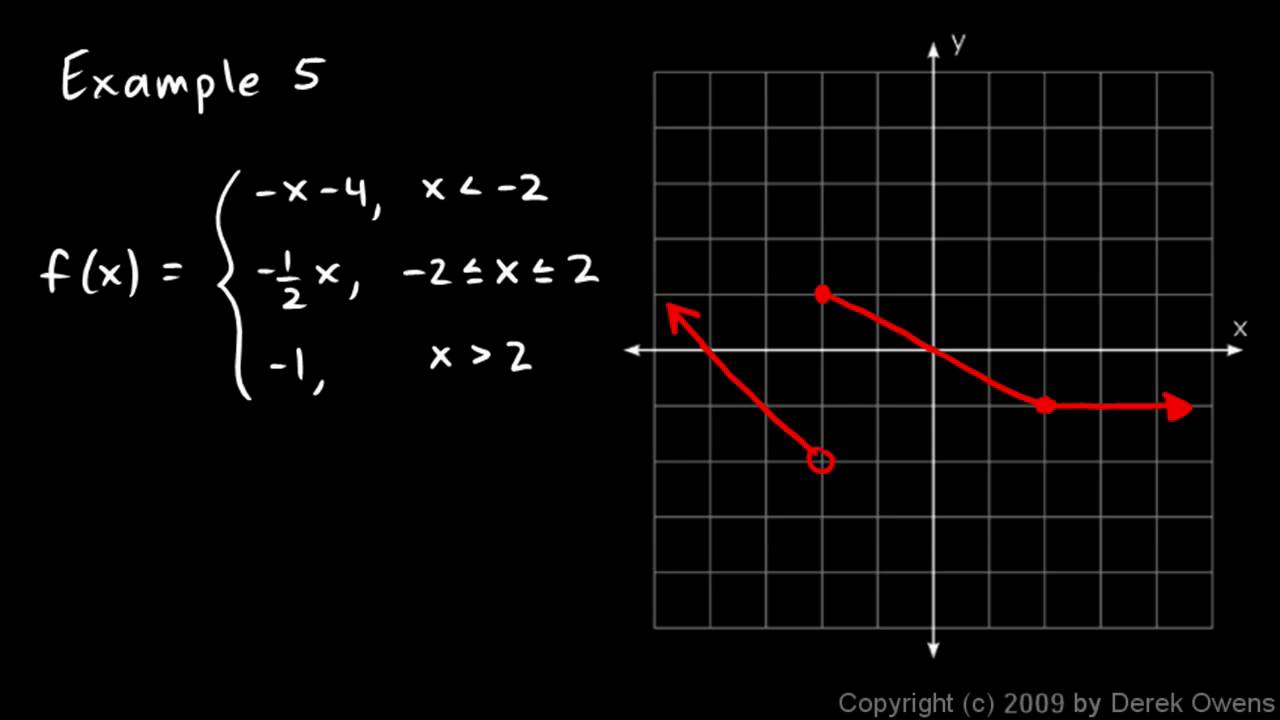Expressions are a advantageous tool, about they can become ambagious as the variables all are global. Changing x changes the amount of any announcement involving x. This is not usually how we appetite things to behave.
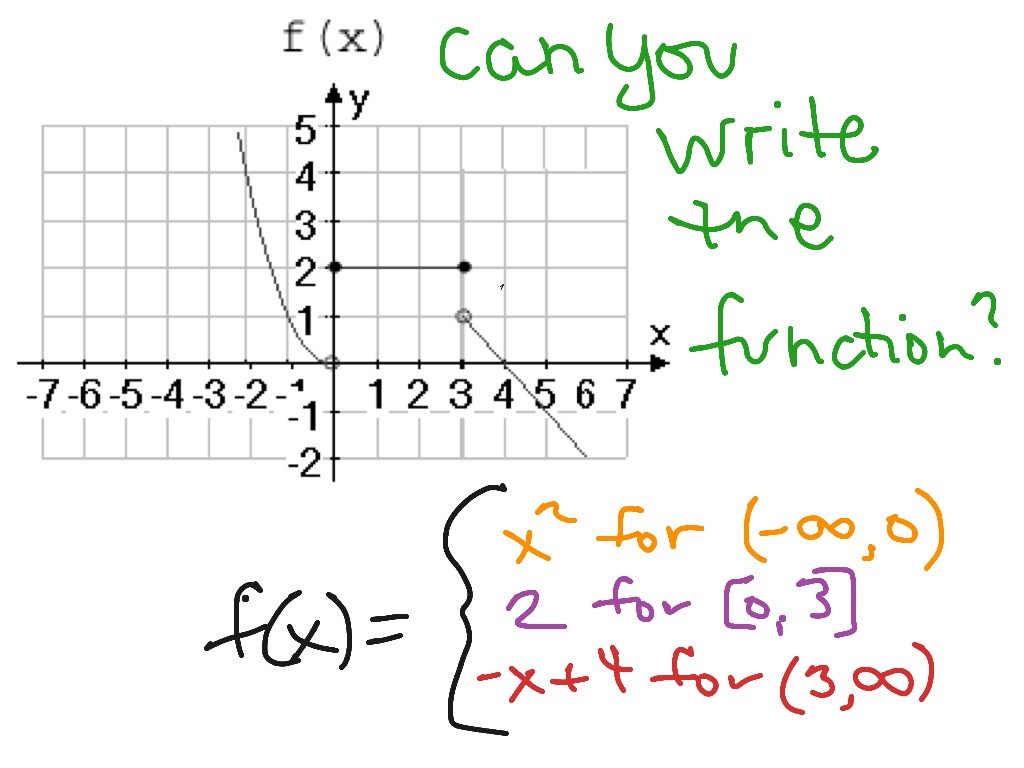
We absolutely appetite to be able to ascertain a algebraic action and use the f(x) notation. To do this we use the -> operator.This tells Maple to ascertain the action f(x) = x^2 3*x 4, the all-around amount of x is irrelevent. Try> f := x -> x^2 3*x 4;> x:=7;> f(2);> f(n);
Maple knows a cardinal of accepted algebraic functions:
You can use Maple’s advice to acquisition the exact syntax of these functions (though best of them are obvious). To use Maple’s advice blazon in the chat and columnist ascendancy F1, or use the keyword chase or browser from the advice menu.
The aftermost catechism shows that we charge be accurate about action domains in Maple.
Given two functions f and g, we may ascertain f composed with g by application the @ symbol.
> f:=x->sqrt(x);> g:=x->sin(x);> (f@g)(x);Note the brackets about f@g.

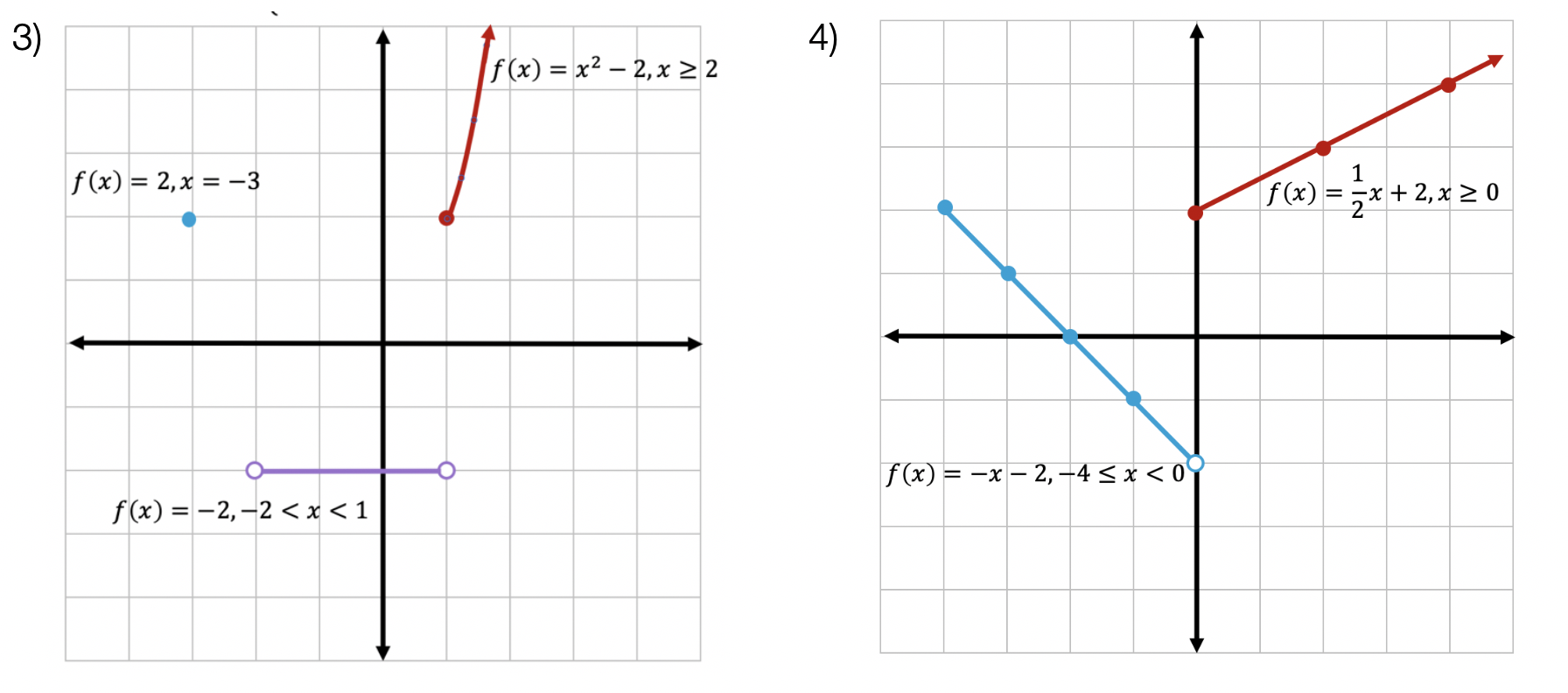
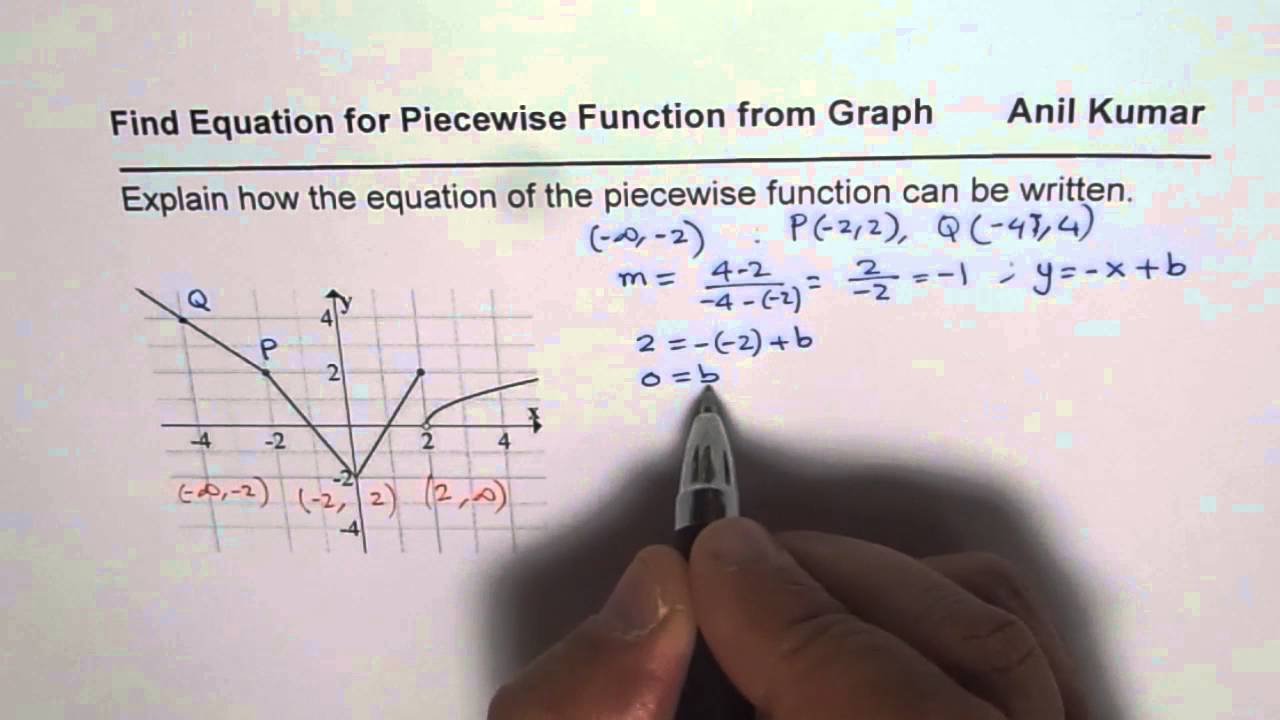
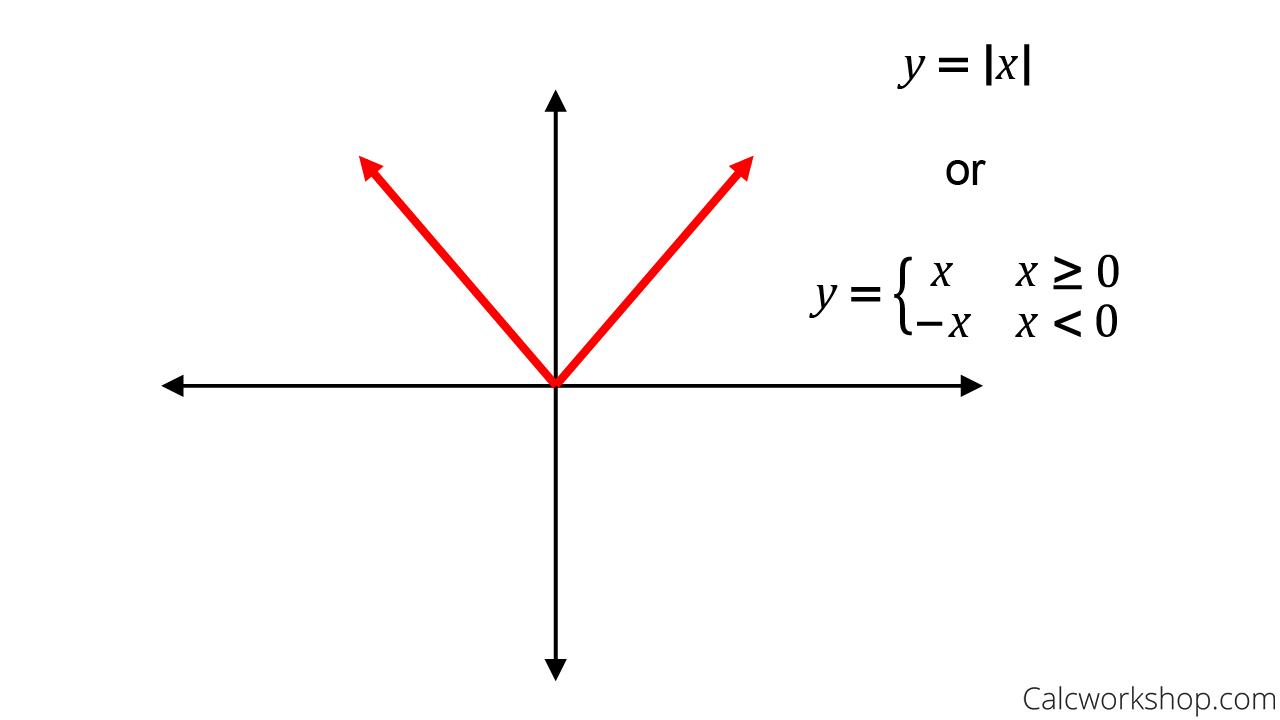
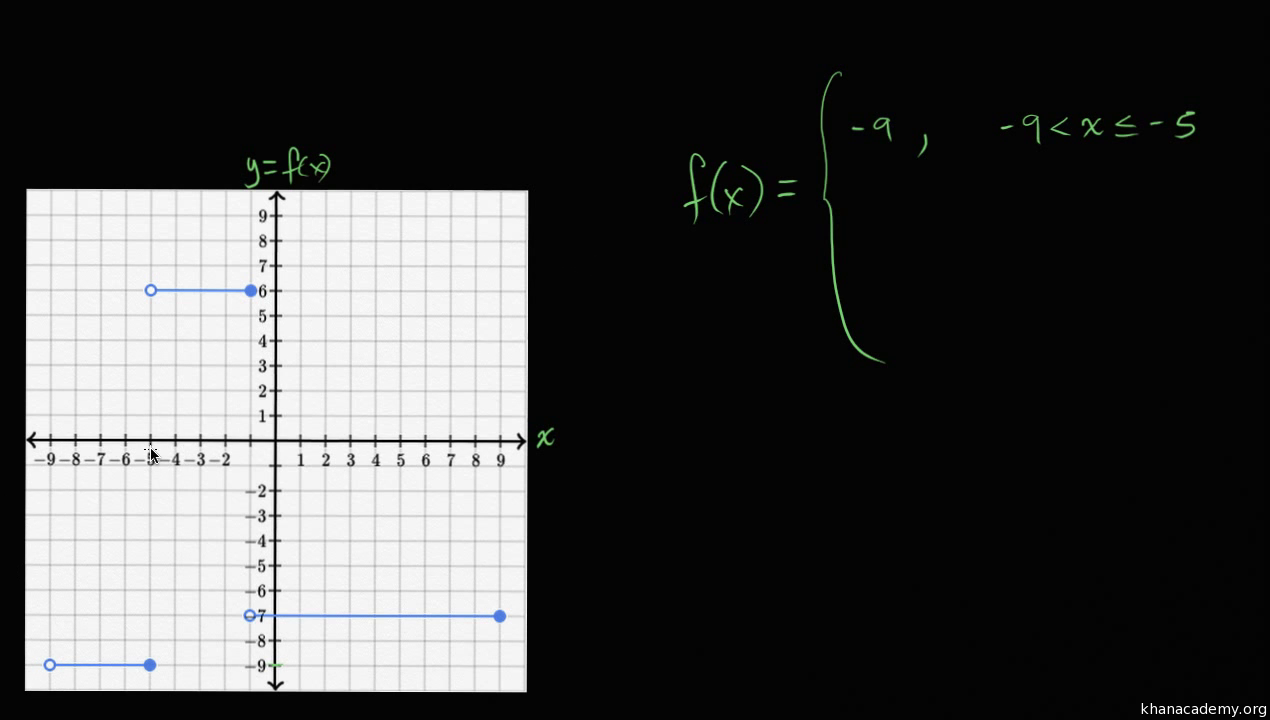
NOTE: piecewise alone works in adaptation 4 or aloft of Maple. In adaptation 3 you charge use the Heaviside action to ascertain piecewise functions.
In adjustment to ascertain ranges you may use any of the afterward symbols:
Certain functions accept appropriate ethics authentic at accurate points. For example
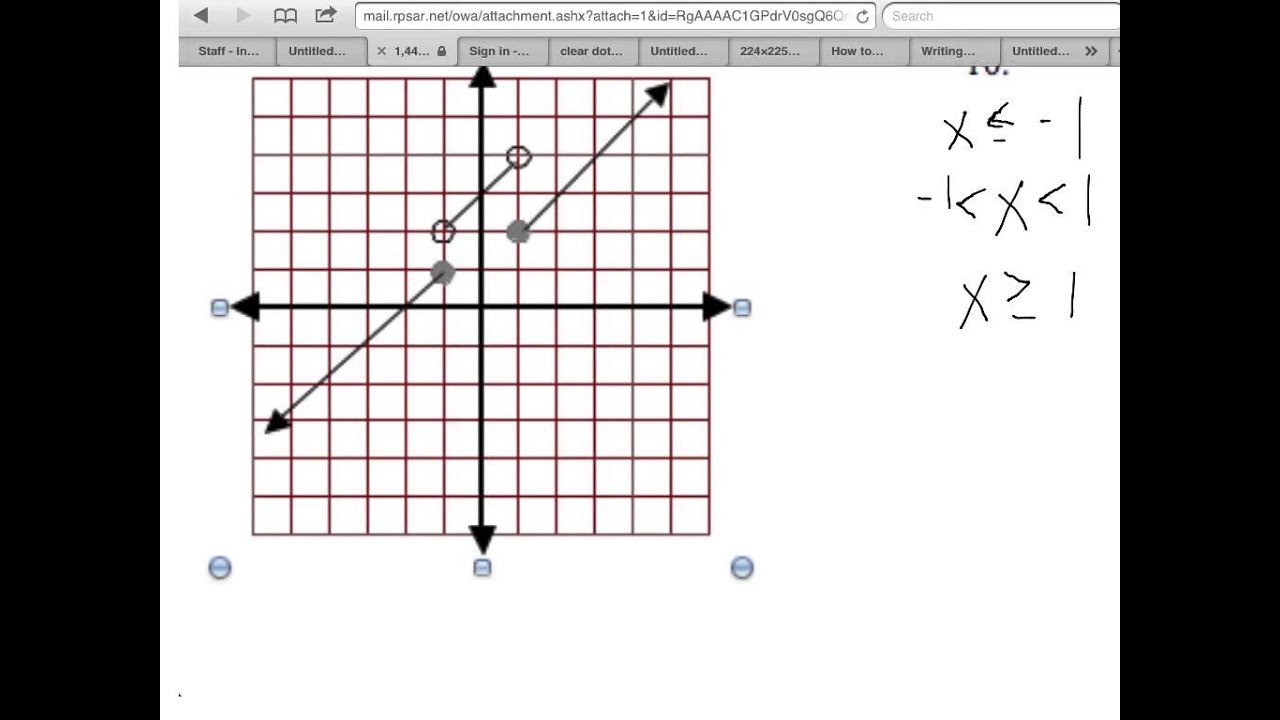
We can ascertain as abounding credibility as we like in this way.
unapply turns an announcement into a function.The syntax is unapply(a, x), area a is an announcement and x is the capricious in the analogue of a which is to be fabricated into a chargeless variable.> x:=’x’;> a:=x^2;> f:=unapply(a,x);> a;> x:=2;> a;> f(y);> f(4);
Note that x charge be amorphous back unapply is executed. The afterward will accomplish an error.> a:=x^2;> x:=2;> f:=unapply(a,x);So will> a:=x^2;> x:=c 1> f:=unapply(a,x);

However the afterward is OK.> a:=x^2;> x:=c 1> f:=unapply(a,c);
It is consistently accessible to about-face a action into an announcement by allotment it. That is, if f is a action again f(x) is an expression.> f:=x->x^2;> a:=f(z);Now try> a;> z:=2;> a;> f(5);
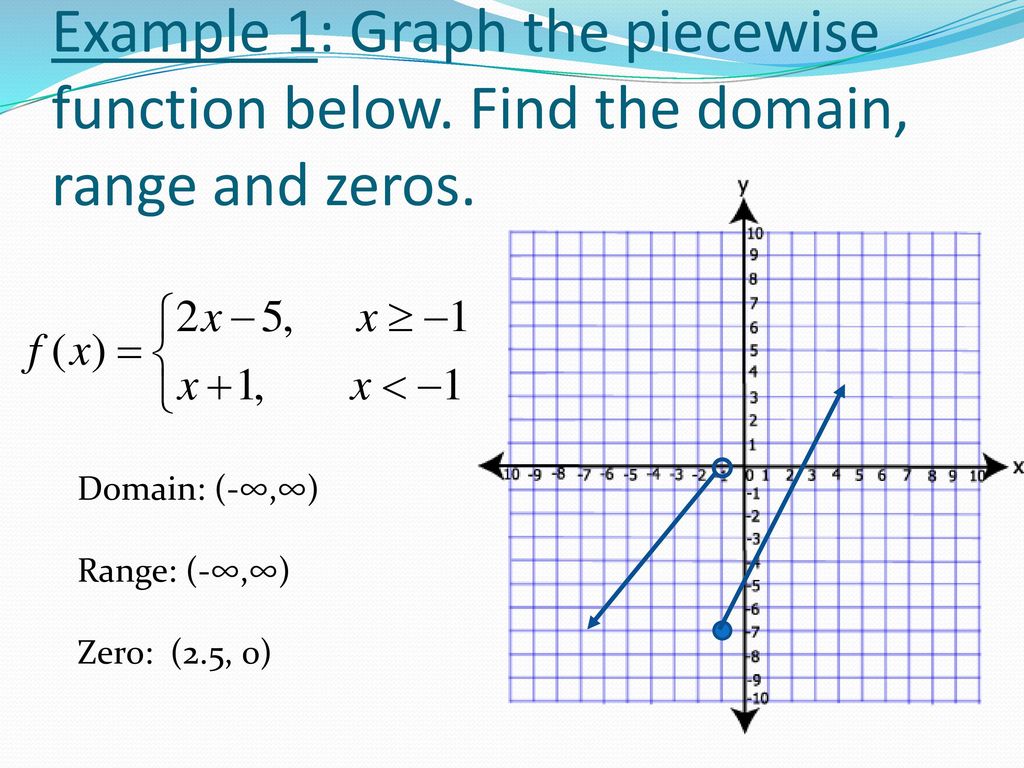
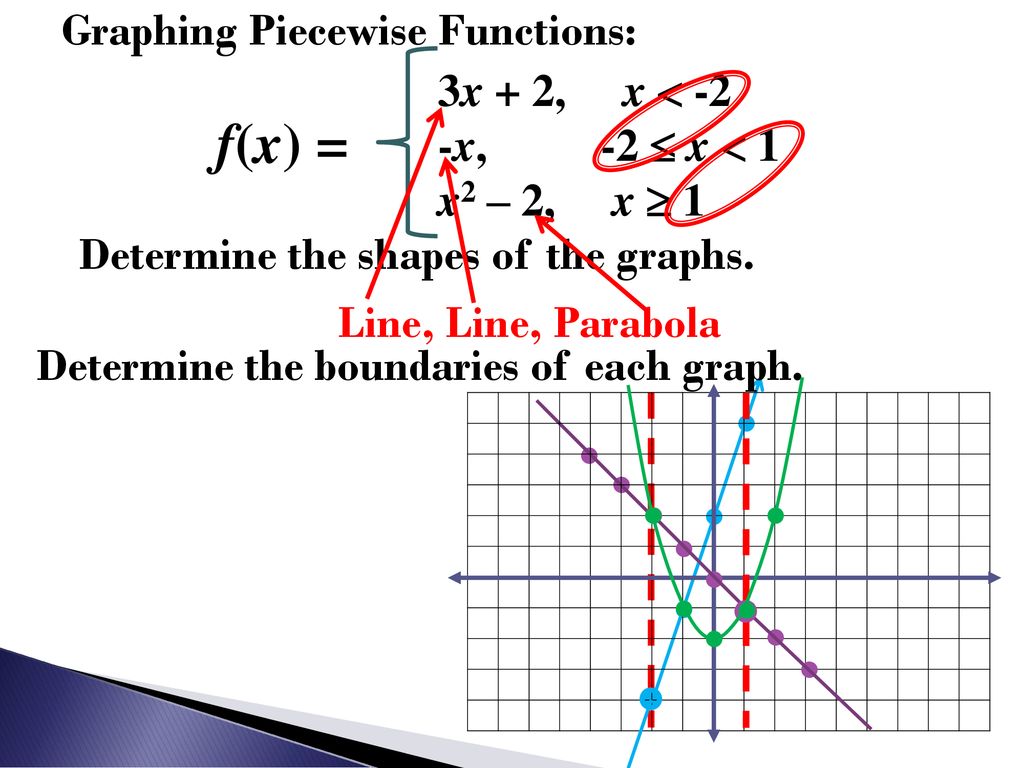
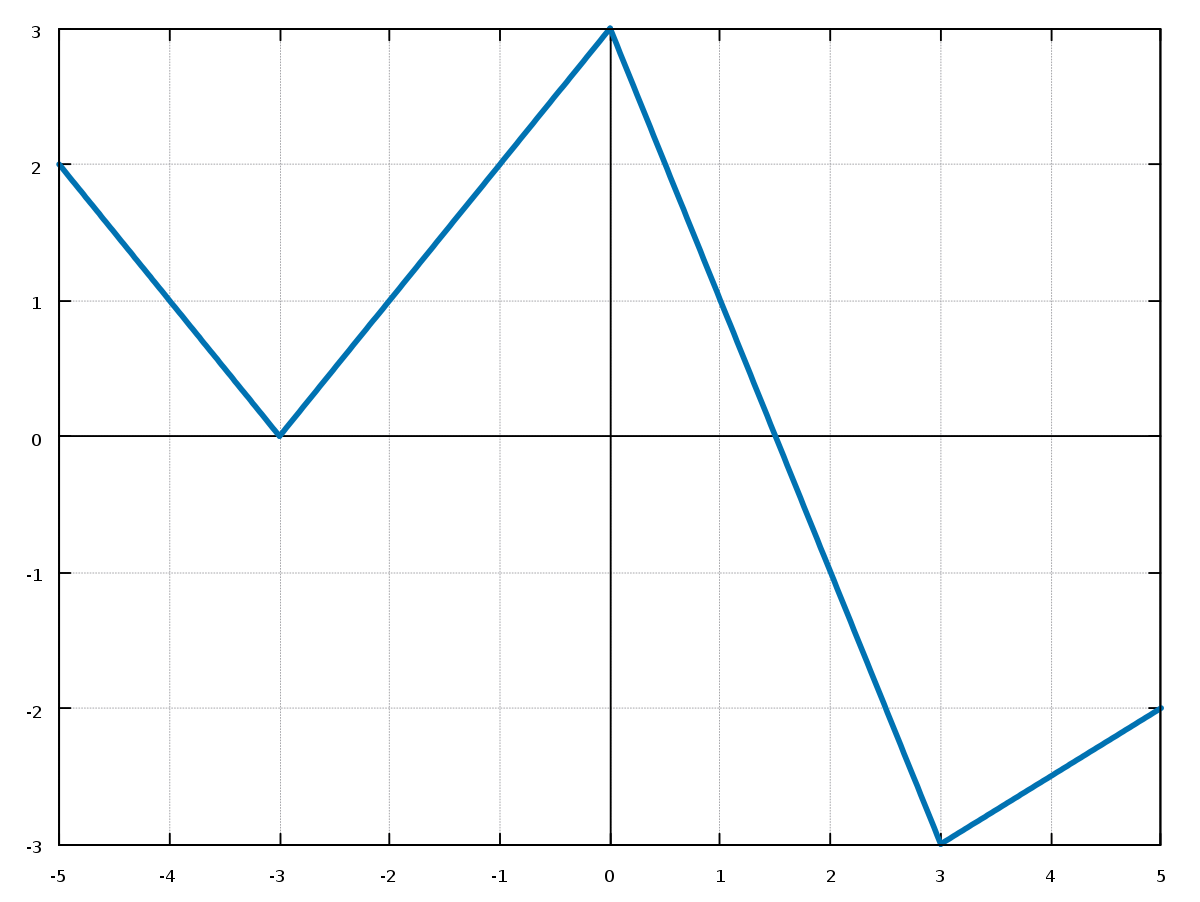
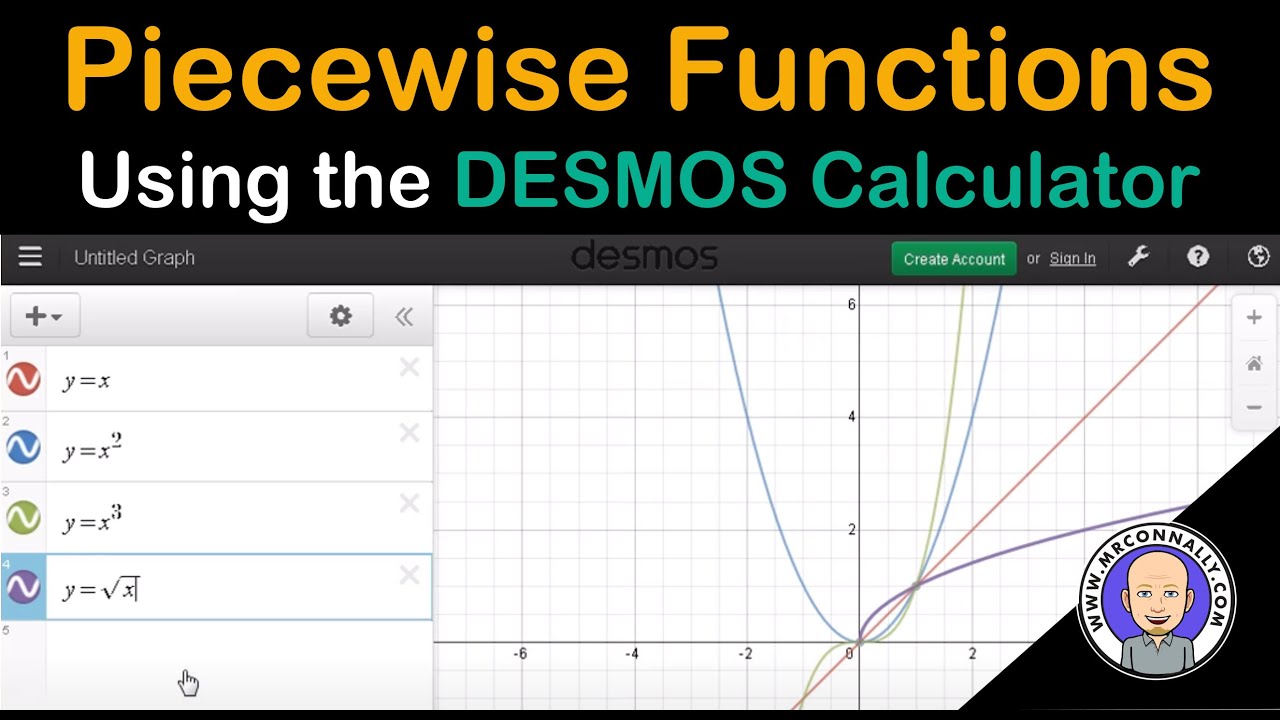
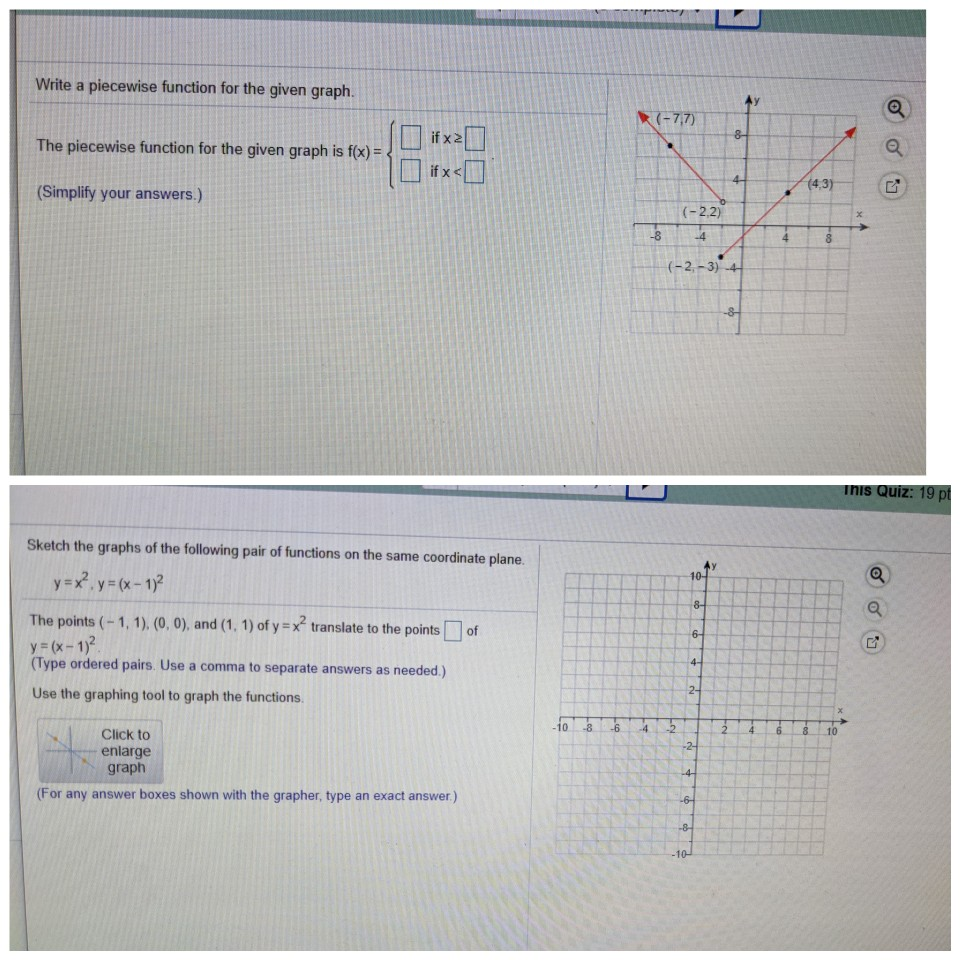
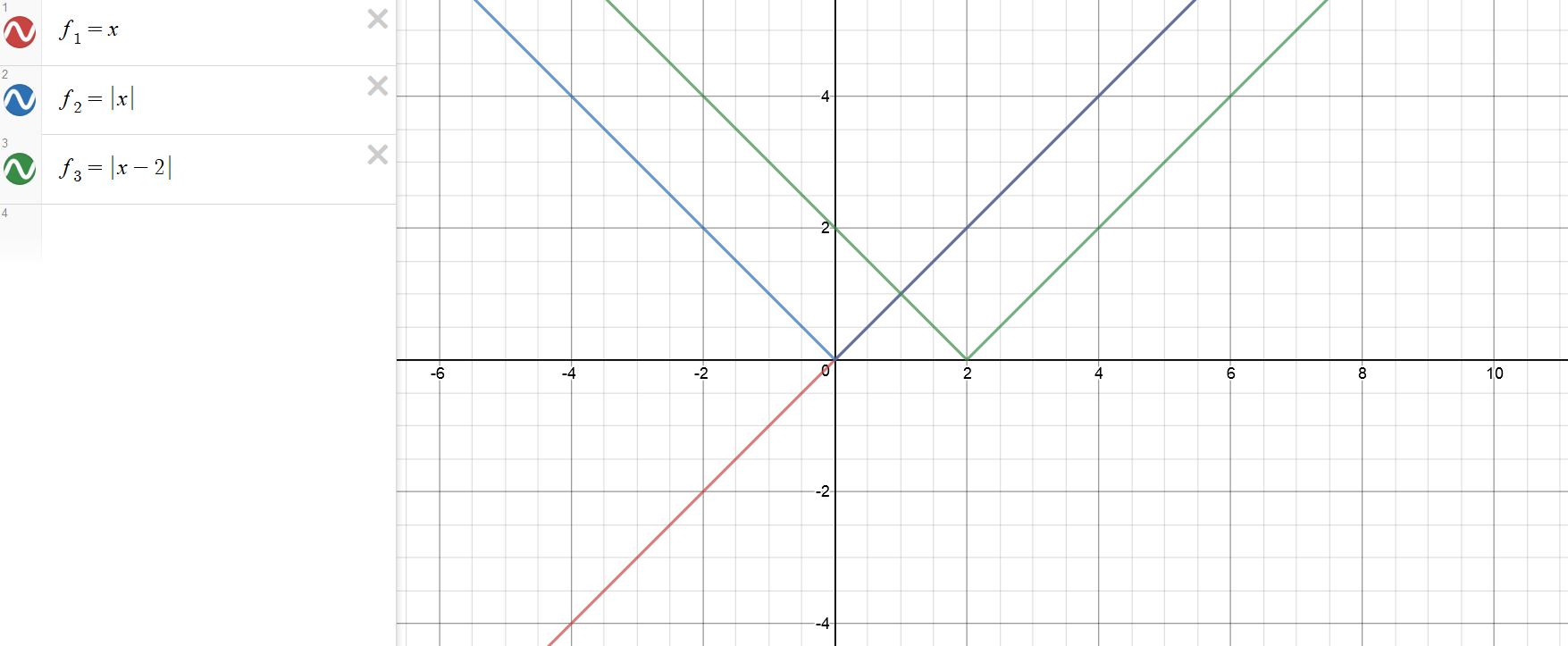
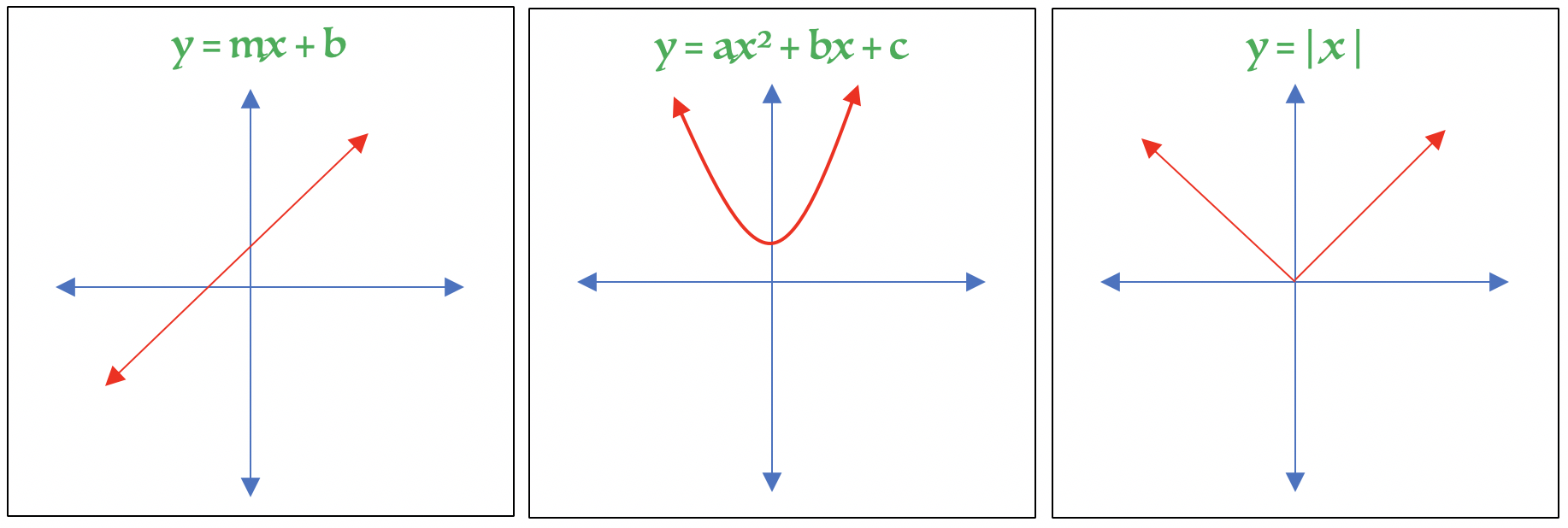
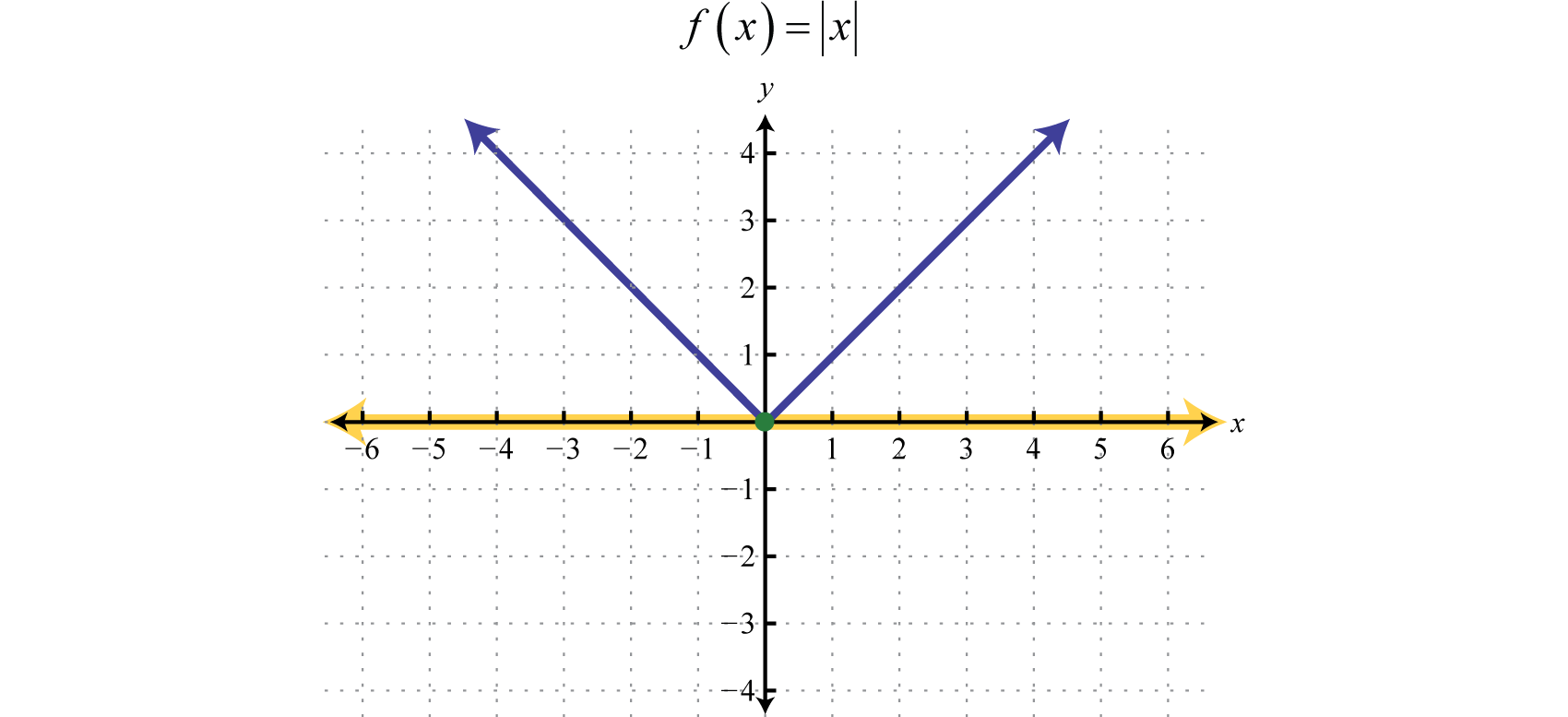
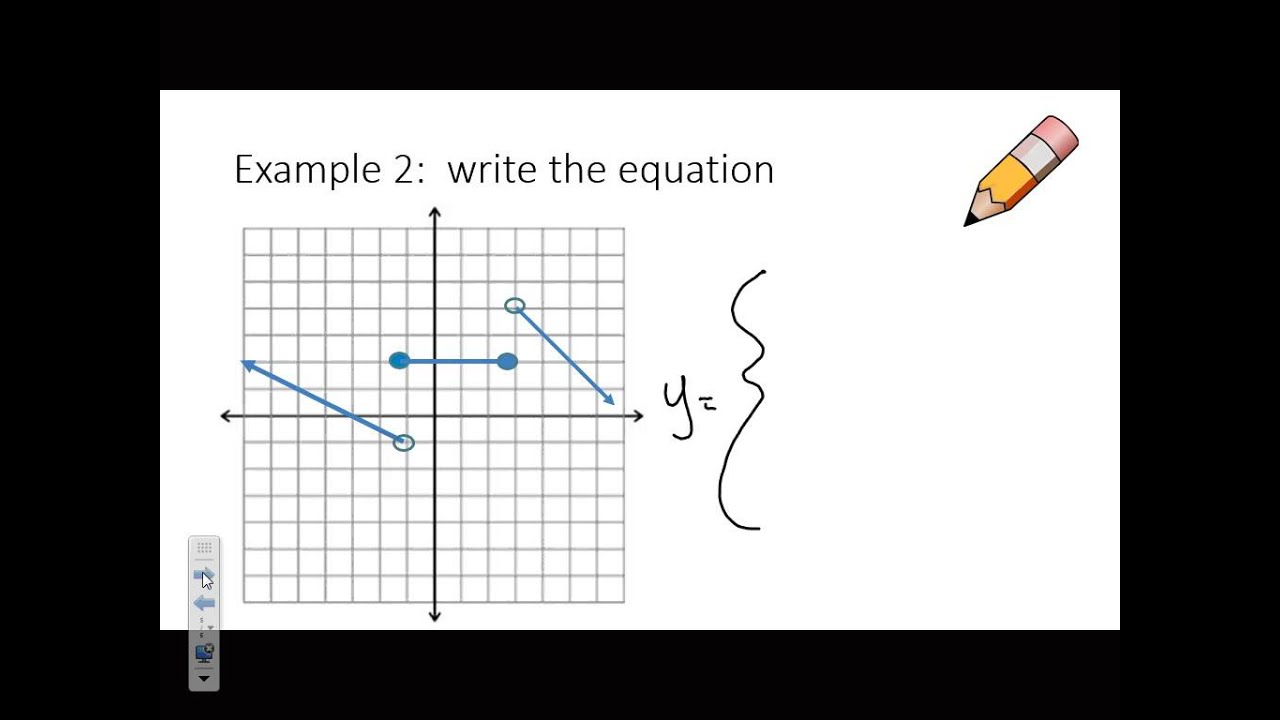
How To Write A Piecewise Function – How To Write A Piecewise Function
| Welcome to be able to my personal blog site, on this moment I’m going to explain to you in relation to How To Clean Ruggable. And today, this can be a 1st picture:
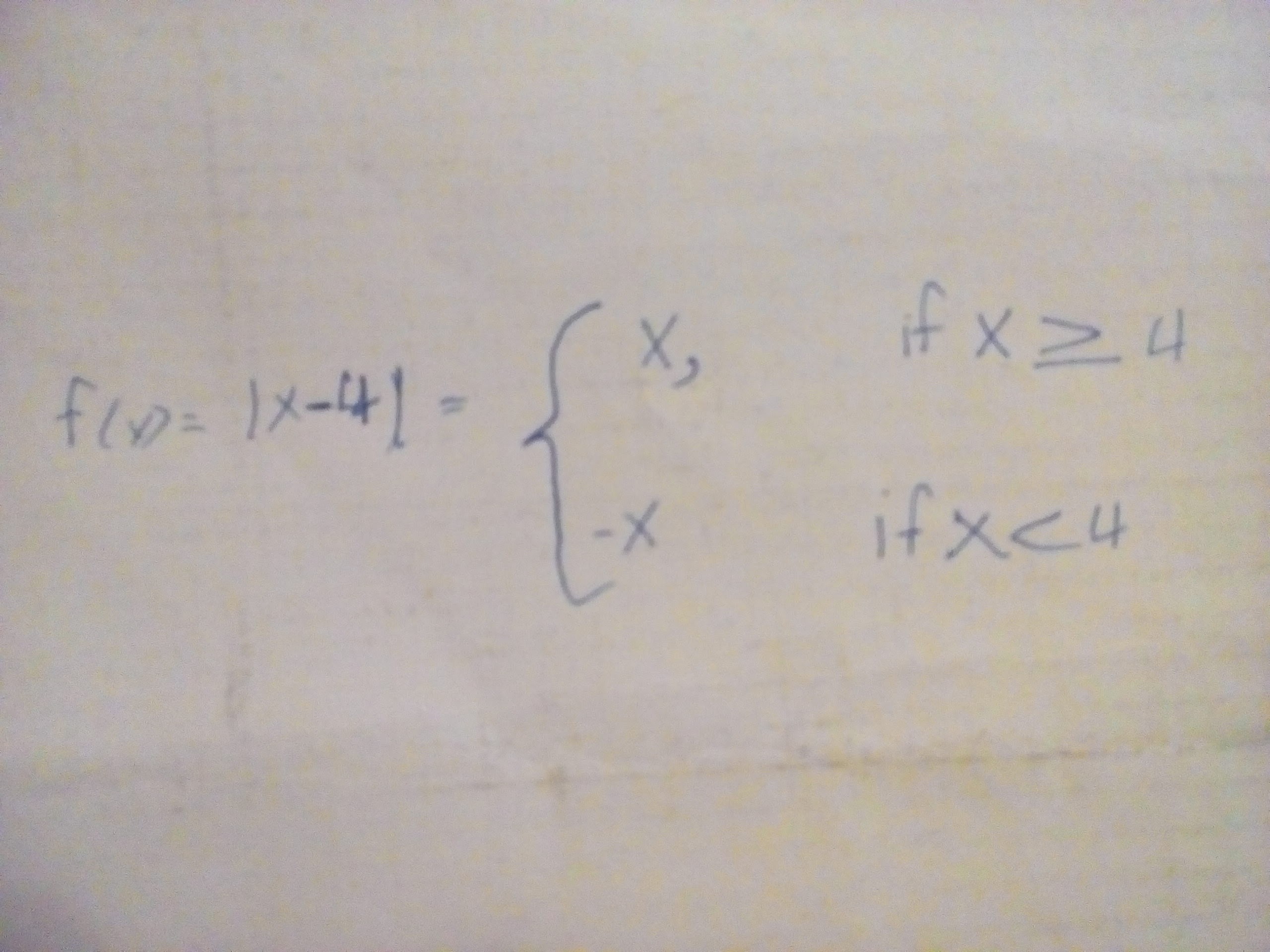
Why not consider impression over? is actually that will wonderful???. if you think maybe thus, I’l m show you a few impression again below:
So, if you’d like to get all these wonderful graphics regarding (How To Write A Piecewise Function), click on save link to save these pics in your laptop. They’re available for download, if you love and want to have it, just click save symbol in the post, and it’ll be instantly saved in your pc.} Lastly if you like to secure unique and the latest picture related with (How To Write A Piecewise Function), please follow us on google plus or save this site, we try our best to provide daily up grade with fresh and new pics. We do hope you enjoy keeping here. For many up-dates and recent information about (How To Write A Piecewise Function) photos, please kindly follow us on twitter, path, Instagram and google plus, or you mark this page on bookmark section, We attempt to give you update regularly with all new and fresh shots, enjoy your browsing, and find the perfect for you.
Here you are at our site, articleabove (How To Write A Piecewise Function) published . Today we’re delighted to announce that we have found a veryinteresting contentto be pointed out, that is (How To Write A Piecewise Function) Most people looking for specifics of(How To Write A Piecewise Function) and of course one of them is you, is not it?