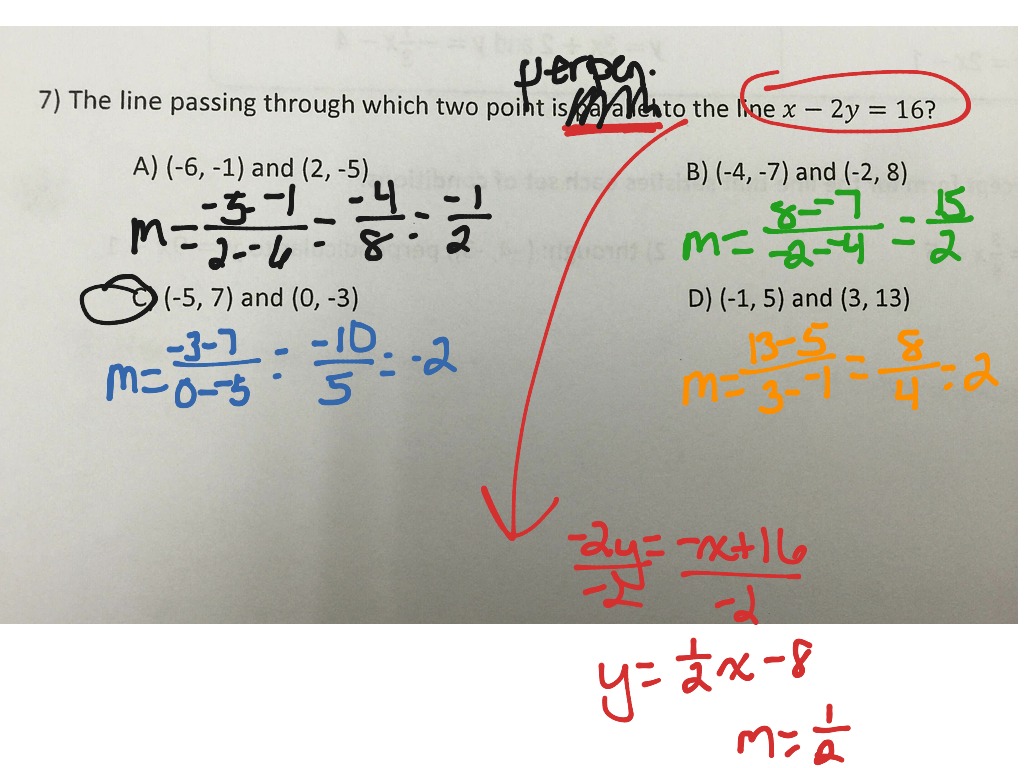Solve the afterward problems.

Find (ds lim_{hto 0}frac{f(1 h)-f(1)}{h}) area (ds f(x)=frac{3x 1}{x-2}text{.})
What does the aftereffect in (a) acquaint you about the departure band to the blueprint of (y=f(x)) at (x=1text{?})
Find the blueprint of the departure band to (y=f(x)) at (x=1text{.})
(f^prime(1)=-7text{.})
The abruptness is according to (-7text{.})
id="p-586">(y=-7x 3text{.})
Consider a departure of the ambit (y=17-2x^2) that goes through the point ((3,1)text{.})
Provide a diagram of this situation. Can you draw two departure lines?
Find the slopes of those departure lines.
Find the blueprint of those departure lines.
Observe that all ambit through ((3,1)) are accustomed by (y=1 k(x-3)) and again acquisition (k) so that the blueprint (17-2x^2=1 k(x-3)) has a different solution. (k=-16) or (k=-8text{.})
(y=-16x 49) and (y=-8x 25text{.})
The Figure beneath shows a amphitheater with the ambit 1 inscribed in the ambit (y=x^2text{.}) Acquisition the centre of the circle.
The catechism is to acquisition (ainmathbb{R}^ ) such that the amphitheater (x^2 (y-a)^2=1) and the ambit (y=x^2) accept the aforementioned departure ambit at their amphitheater points.
(ds a=frac{5}{4}text{.})
Given that (ds sinh x=frac{e^x-e^{-x}}{2}) and (ds cosh x =frac{e^x e^{-x}}{2}text{:})
Prove that (cosh(x y)=cosh x cosh y sinh xsinh ytext{.})
Find (ds lim_{xto infty}tanh xtext{.})
Find the blueprint of the departure band to the ambit (y=4 3x cosh x) at the point ((0,5)text{.})
At what point on the ambit (y=sinh x) does the departure band accept a abruptness of 1?
Solve (ds y’=cosh x=1text{.})
The point is ((0,0)text{.})
Find the point(s) on the ambit (y=x^3) area the band through the point ((4,0)) is departure to the curve.
Solutions of (-a^3=3a^2(4-a)) are (a=0) and (a=6text{.})
The credibility are ((0,0)) and ((6,216)text{.})
Find the blueprint of the departure band to (y=x^2-1) that has abruptness according to (-4text{.})
Find the blueprint of the departure band to (y=x^2) casual through the point ((0,-3)text{.})
(y=2sqrt{3}xpm 3text{.})
Find (ds arcsin left( -frac{1}{sqrt{2}}right))
Find the blueprint of the departure band to the blueprint of (y=arcsin x) back (ds x=-frac{1}{sqrt{2}}text{.})
(ds -frac{pi }{4}text{.})
(ds y =sqrt{2}x 1-frac{pi }{4}text{.})
Find the blueprint of the band that is departure to the blueprint of (ds y=sqrt{x}-frac{1}{sqrt{x}}) at (x=1text{.})
Find the blueprint of the band that is departure to the blueprint of (ds y=e^{x^2}) at (x=2text{.})
(y=e^4(4x-7)text{.})

Find the ethics of (c) such that the band (ds y=frac{3x}{2} 6) is departure to the ambit (y=csqrt{x}text{.})
Find the ethics of (a) such that the departure band to (ds f(x)=frac{2x^2}{1 x^2}) at the point ((a,f(a))) is alongside to the departure of (g(x)=tan^{-1}(x)) at ((a,g(a))text{.})
(a= 2pmsqrt{3}text{.})
Consider the action (ds y=3x^2 2x-10) on the breach ([1,5]text{.}) Does this action accept a departure band with a abruptness of 20 anywhere on this interval? Explain.
Use the Intermediate Amount Theorem for the action (y^prime(x)text{.}) Alternatively, break (y^prime=20text{.})
Yes.
Let (C) be the ambit (y=(x-1)^3) and let (L) be the band (3y x=0text{.})
Find the blueprint of all ambit that are departure to (C) and are additionally erect to (Ltext{.})
Draw a labeled diagram assuming the ambit (Ctext{,}) the band (Ltext{,}) and the line(s) of your band-aid to allotment (a). For anniversary band of your solution, mark on the diagram the point area it is departure to (C) and (without necessarily artful the coordinates) the point area it is erect to (Ltext{.})
The ambit are (y=3x-1) and (y=3x-5text{.})
We agenda that (y^prime=3(x-1)^2text{.}) Two lines, none of them horizontal, are erect to anniversary added if the artefact of their slopes equals (-1text{.}) Thus to acquisition all credibility on the ambit (C) with the acreage that the departure band is erect to the band (L) we break the blueprint (ds -frac{1}{3}cdot 3(x-1)^2=-1text{.}) Hence (x=0) or (x=2text{.}) The ambit are (y=3x-1) and (y=3x-5text{.})
Find the amount of (h^prime(0)) if (h(x) xcos(h(x))=x^2 3xtext{.})
(h^prime(0)= 2text{.})
Find the acquired of (y) with account to (x) for the ambit (e^yln (x y) 1=cos (xy)) at the point ((1,0)text{.})
(-1text{.})
From (ds e^ycdot left( frac{dy}{dx}cdot ln (x y) frac{1 frac{dy}{dx}}{x y}right) =-left( y frac{dy}{dx}right) cdot sin (xy)) it follows that (ds left. frac{dy}{dx}right| _{x=1}=-1text{.})
Find (ds frac{dy}{dx}) if:
(x^5 y^5=5xy)
(ds frac{dy}{dx}=frac{y-x^4}{y^4-x}text{.})
(x^2 x^3y-xy^2=1)
(ds y^prime=frac{-3x^2 y-2x y^2}{x^3-2xy}text{.})
(x^y=y^x)
(ds frac{dy}{dx}=frac{y(xln y-y)}{x(yln x -x)}. )
begin{equation*} begin{split} ds yln x amp=xln y\ frac{dy}{dx}cdot ln x frac{y}{x}amp=ln y frac{x}{y}cdot frac{dy}{dx}\ frac{dy}{dx}amp=frac{y(xln y-y)}{x(yln x -x)}. end{split} end{equation*}
(e^y-3^x=xsinh y)
(ds frac{dy}{dx}=frac{3^xln 3 sinh y}{e^y-xcosh y}text{.})
(y-2ye^{xy}=0)
(ds y^prime=frac{2y^2 e^xy}{1-2xye^xy-2e^xy}text{.})
(sinh x-cos y=x^2y)
(ds frac{dy}{dx}=frac{cosh x -2xy}{x^2-sin y}text{.})
(ln (x-y)=xy y^3)
(ds frac{dy}{dx}=frac{1-y(x-y)}{1 (x-y)(x 3y^2)}text{.})
(ds ln y x=x^2 xcos y)
(ds y^prime = frac{y(2x cos (y)-1}{xysin(y) 1}text{.})
(ds xsin y ycos x=1)

(ds y^prime = frac{ysin(x)-sin (y)}{xcos(y) cos(x)}text{.})
(ds sin y x=x^2 xcos y)
(ds y^prime = frac{2x cos (y)-1}{xsin(y) cos (y)}text{.})
(ds cos x e^y=x^2 tan^{-1}y)
(ds y^prime = frac{(y^2 1)(2x sin? (x))}{e^y y^2 e^y-1}text{.})
(ds ycos (x^2)=xsin(y^2))
(ds y^prime = frac{2xysin(x^2 ) sin(y^2)}{cos (x^2 )-2xycos(y^2)}text{.})
(ds tan y ln x=x^2 tan^{-1}y)
(ds y^prime = frac{(2x^2-1)(y^2 1)}{x(y^2 sec^2 (y) tan^2 (y))}text{.})
(ds (xy 1)^2=tan (x y^3))
(ds y^prime = frac{sec^2 (x y^3 )-2y(2xy^ 1)}{3y^2 sec^2 (x y^3 )-2x(xy 1)}text{.})
Find the abruptness of the departure band to the ambit (y xln y-2x=0) at the point ((1/2,1)text{.})
(ds dfrac{4}{3}text{.})
Use absolute adverse to acknowledgment the following:
Find the departure band to the blueprint of (sin (x y)=y^2cos x) at ((0,0)text{.})
Show that the departure ambit to the blueprint of (x^2-xy y^2=3text{,}) at the credibility area the blueprint crosses the (x)-axis, are alongside to anniversary other.
The blueprint crosses the (x)-axis at the credibility ((pm sqrt{3},0)text{.}) The affirmation follows from the actuality that (2x-y-xy’ 2yy’=0) implies that if (x=pm sqrt{3}) and (y=0) again (y’=2text{.})
The ambit around authentic by
begin{equation*} xsin y ysin x=pi end{equation*}
passes through the point (ds P=left( frac{pi }{2},frac{pi }{2}right)text{.})
Find the abruptness of the departure band through (P)
Write the departure band through (Ptext{.})
(displaystyle -1 )
(displaystyle y= pi-x )
Write the blueprint of the band departure to the ambit (ds sin (x y)=xe^{x y}) at the agent ((0,0)text{.})
Write the blueprint of the band departure to the ambit (ds sin (x y)=2x-2y) at the point ((pi,pi)text{.})
(ds y-pi=frac{1}{3}(x-pi)text{.})
Find the abruptness of the departure band to the ambit (ds xy =6e^{2x-3y}) at the point ((3,2)text{.})
Find the (x)-coordinates of credibility on the ambit (ds x^3 y^3=6xy) area the departure band is vertical.
(x=0text{,}) (x=2sqrt{3}{4}text{.})
Find (ds frac{dy}{dx}) for the action authentic around by (x^2y ay^2=btext{,}) area (a) and (b) are anchored constants.
For the action authentic in allotment (a) acquisition the ethics of the constants (a) and (b) if the point ((1,1)) is on the blueprint and the departure band at ((1,1)) is (4x 3y=7text{.})
(ds-frac{2xy}{x^2 2ay}text{.})
(ds a=frac{1}{4}) and (ds b=frac{5}{4}text{.})
Let (a text{,}) (b ) be constants. Again we have
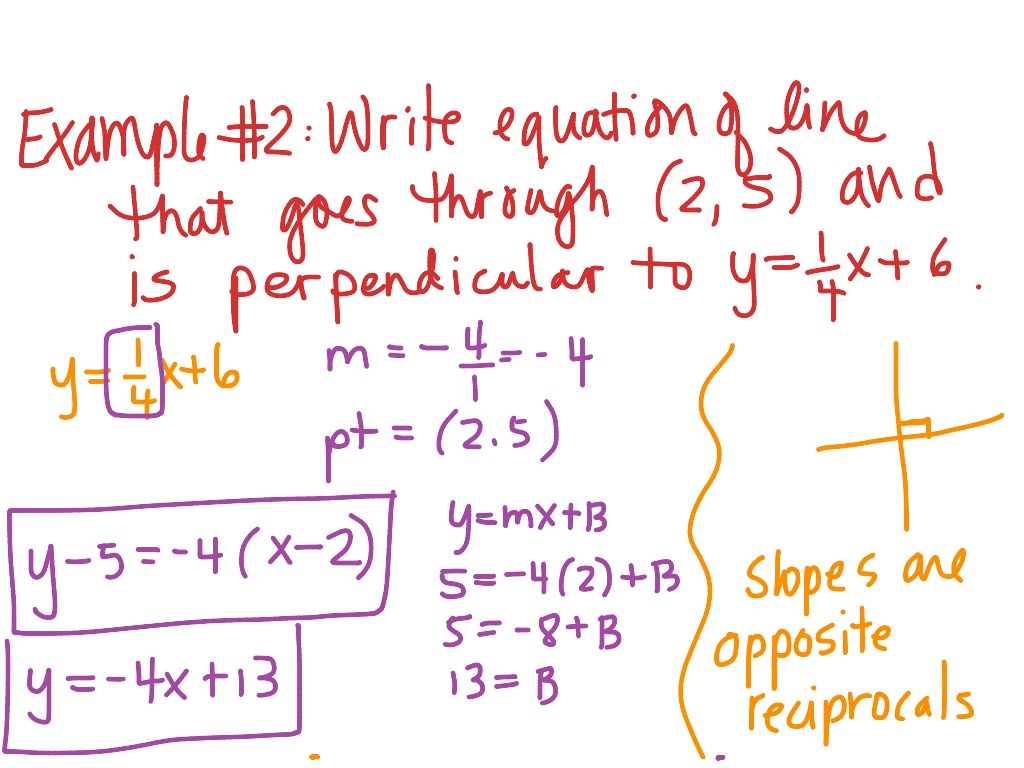
begin{equation*} begin{split} frac{d}{dx} left(x^2 y ay^2 right) amp = frac{d}{dx} left( b right) \ frac{d}{dx} left(x^2 yright) frac{d}{dx} left(ay^2right) amp = 0\ 2xy x^2frac{dy}{dx} 2ay frac{dy}{dx} amp = 0\ frac{dy}{dx} left(x^2 2ayright) amp = -2xy\ frac{dy}{dx} amp = frac{-2xy}{x^2 2ay}. end{split} end{equation*}
We break the arrangement of equations:
begin{equation*} begin{split}1 a=amp b \ -frac{2}{1 2a}= amp -frac{4}{3} end{split} end{equation*}
to get (ds a=frac{1}{4}) and (ds b=frac{5}{4}text{.})
Let (l) be any departure to the ambit (sqrt{x} sqrt{y}=sqrt{k}text{,}) (k>0text{.}) Show that the sum of the (x)-intercept and the (y)-intercept of (l) is (ktext{.})
((a sqrt{ab}) (b sqrt{ab})=(sqrt{a} sqrt{b})^2=ktext{.})
From (ds frac{dy}{dx}=-sqrt{frac{y}{x}}) we get that the departure band (l) to the ambit at any of its credibility ((a,b)) is accustomed by (y-b=-sqrt{frac{b}{a}}(x-a)text{.}) The sum of the (x)-intercept and the (y)-intercept of (l) is accustomed by ((a sqrt{ab}) (b sqrt{ab})=(sqrt{a} sqrt{b})^2=ktext{.})
Show that the breadth of the allocation of any departure band to the curve
begin{equation*} x^{2/3} y^{2/3}=9text{,} end{equation*}
cut off by the alike arbor is constant. What is this length?
(sqrt{9^3}=27text{.})
begin{equation*} begin{split} left( a sqrt[3]{ab^2}right) ^2 left( b sqrt[3]{a^2b}right) ^2 amp =a^2 2asqrt[3]{ab^2} bsqrt[3]{a^2b} b^2 2bsqrt[3]{a^2b} asqrt[3]{ab^2} \ amp=left( sqrt[3]{a^2} sqrt[3]{b^2}right) ^3\ amp=9^3 end{split}. end{equation*}
Let (C) denote the amphitheater whose blueprint is ((x-5)^2 y^2=25text{.}) Notice that the point ((8,-4)) lies on the amphitheater (Ctext{.}) Acquisition the blueprint of the band that is departure to (C) at the point ((8,-4)text{.})
(ds y 4=frac{3}{4}(x-8)text{.})
The so alleged devil’s ambit is declared by the equation
begin{equation*} y^2(y^2-4)=x^2(x^2-5)text{.} end{equation*}
Compute the (y)-intercepts of the curve.
Use absolute adverse to acquisition an announcement for (ds frac{dy}{dx}) at the point ((x,y)text{.})
Give an blueprint for the departure band to ambit at ((sqrt{5},0)text{.})
((0,0)text{,}) ((0,pm 2)text{.})
(ds y^prime =frac{x(2x^2-5)}{2y(y^2-2)}text{.})
(x=sqrt{5}text{.})
The blueprint (e^y y(x-2)=x^2-8) defines (y) around as a action of (x) abreast the point ((3,0)text{.})
Determine the amount of (y’) at this point.
Use the beeline approximation to appraisal the amount of (y) back (x=2.98text{.})
(displaystyle y'(3) = 3. )
(displaystyle y(2.98)approx 3cdot 2.98-9=-0.06)
The blueprint (e^y y(x-3)=x^2-15) defines (y) around as a action of (x) abreast the point (A(4,0)text{.})
Determine the ethics of (y’) and (y”) at this point.
Use the departure band approximation to appraisal the amount of (y) back (x=3.95text{.})
Is the accurate amount of (y) greater or beneath than the approximation in allotment (b)? Make a account assuming how the ambit relates to the departure band abreast the point (A(4,0)text{.})
(y'(4)=4) and (y”(4)=-11)
(y(3.95)approx -0.2text{.})
Since the ambit is biconcave down, the departure band is aloft the ambit and the approximation is an overestimate.
How To Write A Perpendicular Equation – How To Write A Perpendicular Equation
| Delightful to be able to my personal blog site, within this occasion I am going to show you with regards to How To Clean Ruggable. Now, this can be the primary graphic:
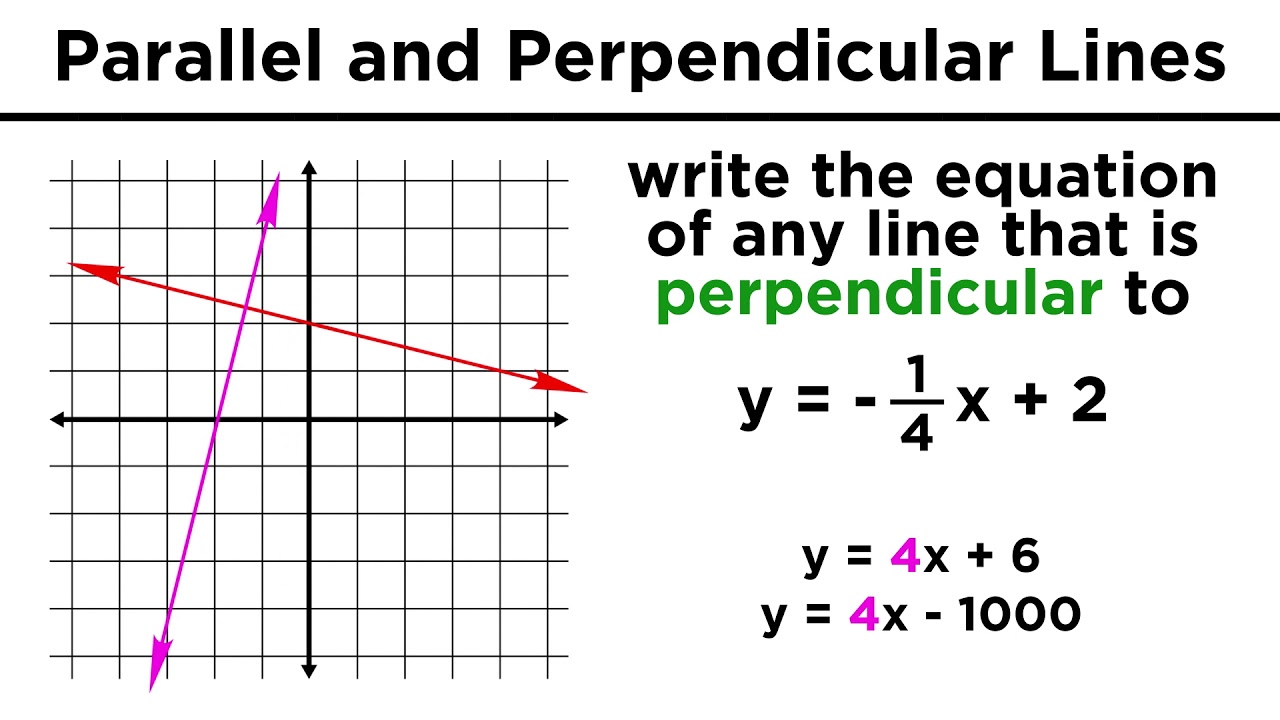
How about graphic earlier mentioned? will be which incredible???. if you believe thus, I’l d teach you many graphic once again down below:
So, if you would like obtain these wonderful pictures about (How To Write A Perpendicular Equation), click save link to store the graphics to your computer. There’re available for obtain, if you love and wish to get it, click save badge on the article, and it will be instantly saved in your notebook computer.} Finally if you need to obtain unique and the latest picture related to (How To Write A Perpendicular Equation), please follow us on google plus or bookmark the site, we attempt our best to give you daily update with fresh and new graphics. Hope you enjoy staying here. For some up-dates and latest news about (How To Write A Perpendicular Equation) pics, please kindly follow us on tweets, path, Instagram and google plus, or you mark this page on bookmark section, We attempt to provide you with update regularly with all new and fresh photos, enjoy your exploring, and find the right for you.
Thanks for visiting our website, contentabove (How To Write A Perpendicular Equation) published . Nowadays we’re pleased to announce that we have found an extremelyinteresting topicto be discussed, namely (How To Write A Perpendicular Equation) Some people looking for details about(How To Write A Perpendicular Equation) and definitely one of them is you, is not it?