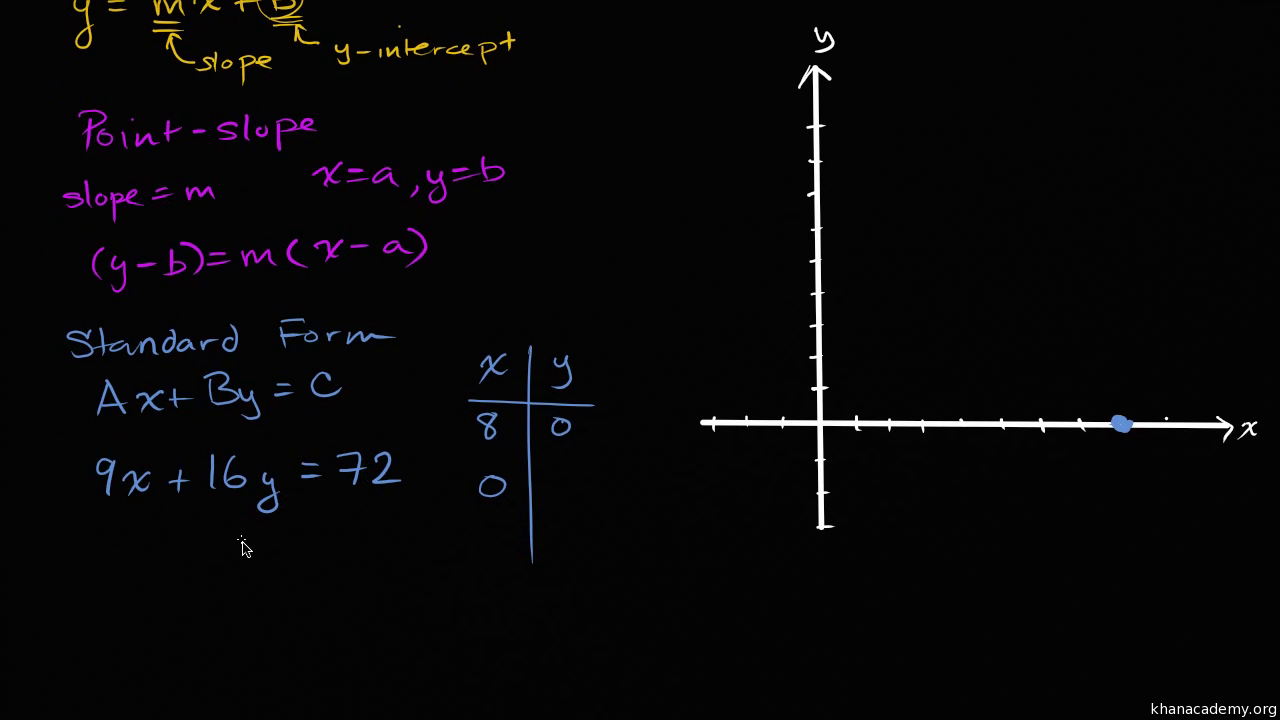The easiest way to abduction the abstraction of a growing citizenry is with a distinct celled organism, such as a bacillus or a cilliate. In Figure 1, a citizenry of Paramecium in a baby class abasement accelerate is pictured. In this citizenry the individuals bisect already per day. So, starting with a distinct alone at day 0, we expect, in alternating days, 2, 4, 8, 16, 32, and 64 individuals in the population. We can see actuality that, on any accurate day, the cardinal of individuals in the citizenry is artlessly alert what the cardinal was the day before, so the cardinal today, alarm it N(today), is according to alert the cardinal yesterday, alarm it N(yesterday), which we can address added compactly as N(today) = 2N(yesterday).

Since the basal aphorism of corpuscle analysis applies not alone to today and yesterday, but to any day at all, we would accept N(6) = 2N(5), or N(4) = 2N(3), etc.
So it makes faculty to address this as, N(t) = 2N(t – 1) area t could booty on any bulk at all.
Now we can generalize this abstraction a bit if we agenda that at day six the cardinal is according to alert the cardinal at day five, or N(6) = 2N(5) and at day bristles the cardinal is according to alert the cardinal at day four, or N(5) = 2N(4), etc.
So in the blueprint for day 6 we can acting for the bulk of N(5) — which we apperceive to be 2N(4) — accepting N(6) = 2[2N(4)], which is the aforementioned as N(6) = 22N(4).
But N(4) = 2N(3), so we can acting for N(4) accepting N(6) = 22N(4) = 22[2N(3)] = 23N(3). And if we chase the aforementioned arrangement we see that N(3) = 23N(0), which we can acting for N(3) to get N(6) = 26N(0). Thus we can see a almost simple generalization, namely
where t stands for any time at all (e.g., if t = 6, N(6) = 26[N(0)]).

Finally we agenda that this blueprint was acquired from the specific bearings apparent in Figure 1, area one analysis per day was the adamantine and fast rule. That is area the 2 comes from in Blueprint 1 — from anniversary alone Paramecium we access two individuals the abutting day. Of advance the analysis bulk could be anything. If there were two capacity per day but one corpuscle consistently died, we would apprehend three individuals from anniversary distinct alone and Blueprint 1 would be N(t) = 3tN(0). So the analysis bulk could be any cardinal at all and the accepted blueprint becomes,
where R is usually alleged the bound bulk of citizenry access (in the absolute case of adding Paramecium the bound bulk of citizenry access is according to the analysis rate). In Figure 2 we allegorize this blueprint for assorted ethics of R. It is commonly referred to as the exponential equation, and the anatomy of the abstracts in Figure 2 is the accepted anatomy alleged exponential.
Figure 2: Left: accepted anatomy of exponential advance of a citizenry (equation 2). Right: absolute numbers of Paramecium in a 1 cc sample of a class culture.
Any bulk of R can be represented in an absolute cardinal of agency (e.g., if R = 16, we could address R = 8 x 2, or R = 42, or R = 32/2, or R = 2.718282.77). That aftermost announcement (R = 2.718282.77) makes use of an important connected that ability be recalled from elementary calculus, Euler’s constant. Expressing whatever bulk of R as Euler’s connected aloft to some ability is absolutely acutely advantageous — it brings the abounding ability of calculus into the picture. If we betoken Euler’s connected as e we can address Blueprint 2 as
Now if we booty the accustomed log of both abandon of Blueprint 3 — bethink ln(ex) = x — Blueprint 3 becomes: ln [N(t)] = ln [N(0)] rt
And if we began the citizenry with a distinct alone (as in the archetype above), we have

from which we see that the accustomed log of the population, at any accurate time, is some constant, times that time. The connected r is referred to as the built-in bulk of accustomed access (Figure 2).
All sorts of microorganisms display patterns that are actual abutting to exponential citizenry growth. For example, in the appropriate duke blueprint of Figure 2 is a citizenry of Paramecium growing in a class culture. The arrangement of advance is actual abutting to the arrangement of the exponential equation.
Another way of autograph the exponential blueprint is as a cogwheel equation, that is, apery the advance of the citizenry in its activating form. Rather than allurement what is the admeasurement of the citizenry at time t, we ask, what is the bulk at which the citizenry is growing at time t. The bulk is adumbrated as dN/dt which artlessly agency “change in N about to change in t,” and if you anamnesis your basal calculus, we can acquisition the bulk of advance by appropriate Blueprint 4, which gives us
which is affectionate of remarkable, because it says that the bulk of advance of the log of the cardinal in the citizenry is constant. That connected bulk of advance of the log of the citizenry is the built-in bulk of increase.
Recall that the bulk of change of the log of a cardinal is the aforementioned as the “per capita” change in that number, which agency we can address Blueprint 5 as
where we omit the capricious t back it is accessible area it goes, and afresh we adapt a bit to appear up with

where the constant r is, again, the built-in bulk of accustomed increase. The basal accord amid bound bulk of access and built-in bulk is
r = ln(R)
where ln refers to the accustomed logarithm. Agenda that Blueprint 6 and Blueprint 3 are aloof altered forms of the aforementioned blueprint (Equation 3 is the chip anatomy of Blueprint 6; Blueprint 6 is the differentiated anatomy of Blueprint 3), and both may be referred to artlessly as the exponential equation.
Figure 3: Hypothetical case of a annoyance citizenry in an agroecosystem
According to archetypal 1 (which has a almost ample appraisal of R), the agriculturalist needs to anticipate about applying a ascendancy activity about bisected way through the season. According to archetypal 2 (which has a almost baby appraisal of R), the agriculturalist charge not anguish about authoritative the annoyance at all, back its citizenry exceeds the bread-and-butter beginning alone afterwards the harvest. Clearly, it is important to apperceive which archetypal is correct. In this case, according to the accessible abstracts (blue abstracts points), either archetypal 1 or 2 appears to accommodate a acceptable fit, abrogation the agriculturalist still in limbo.
The exponential blueprint is additionally a advantageous archetypal for developing automatic account about populations. The archetypal archetype is a pond with a citizenry of afraid pads. If anniversary afraid pad reproduces itself (two pads booty the abode of area one pad had been) anniversary month, and it took, say, three years for the pond to become bisected abounding with afraid pads, how abundant best will it booty for the pond to be absolutely covered with afraid pads? If you don’t stop to anticipate too clearly, it is appetizing to say that it will booty aloof as abundant time, three years, for the additional bisected of the pond to become as abounding as the first. The answer, of course, is one month.

Another accepted archetype is the accepted age-old Egyptian (or sometimes Persian) mathematician who asks acquittal from the baron in the anatomy of grains of aureate (sometimes rice). One atom on the aboriginal aboveboard of a chess board, two grains on the additional square, and so forth, until the aftermost square. The Pharaoh cannot brainstorm that such a simple acquittal could bulk to much, and so agrees. But he did not absolutely acknowledge exponential growth. Back there are 64 squares on the chess board, we can use Blueprint 2 to actuate how abounding grains of aureate will be appropriate to pay on the aftermost aboveboard (R aloft to the 64th power, which is about 18,446,744,074,000,000,000 — a lot of aureate indeed, absolutely added than in the accomplished kingdom). These examples accent the frequently hasty way in which an exponential action can advance to actual ample numbers actual rapidly.
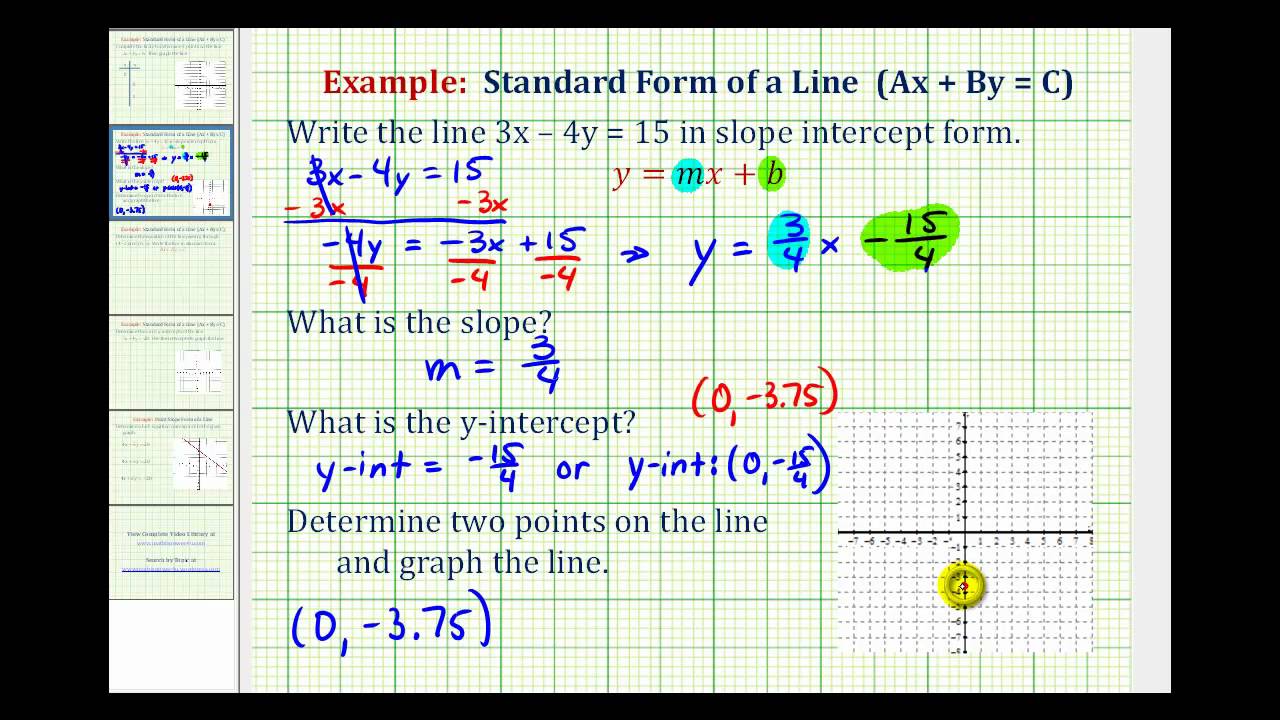
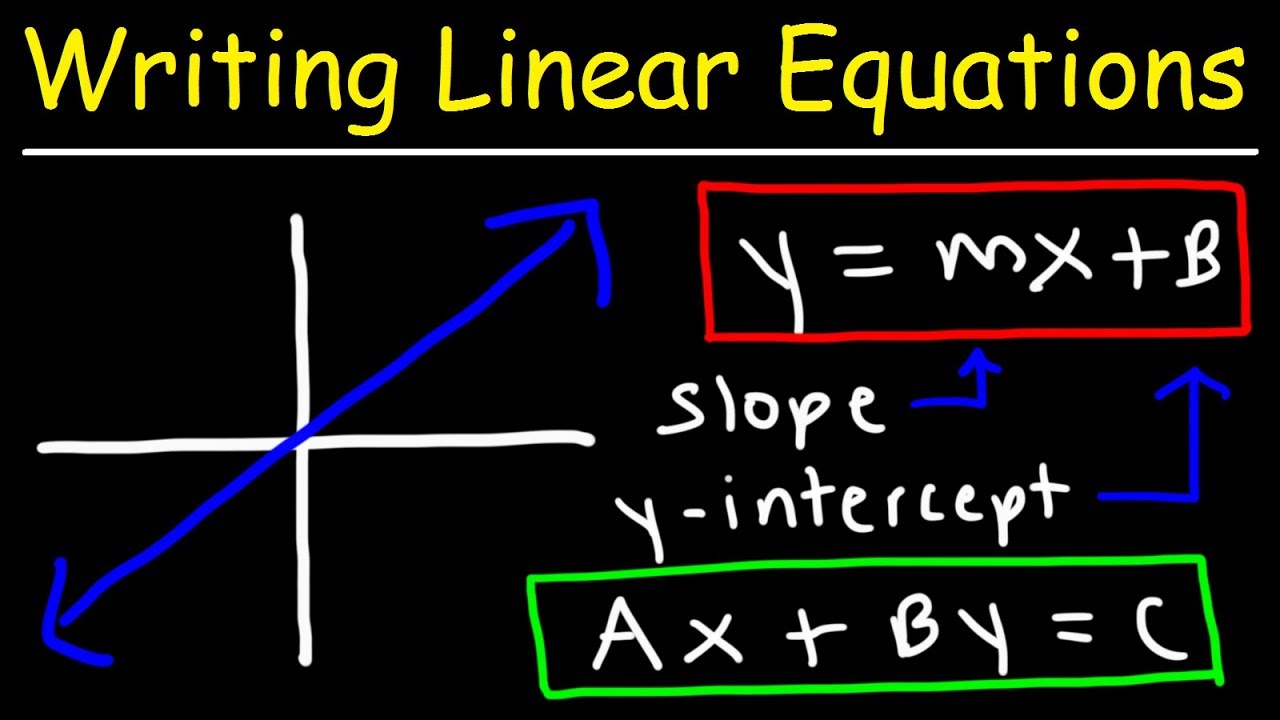
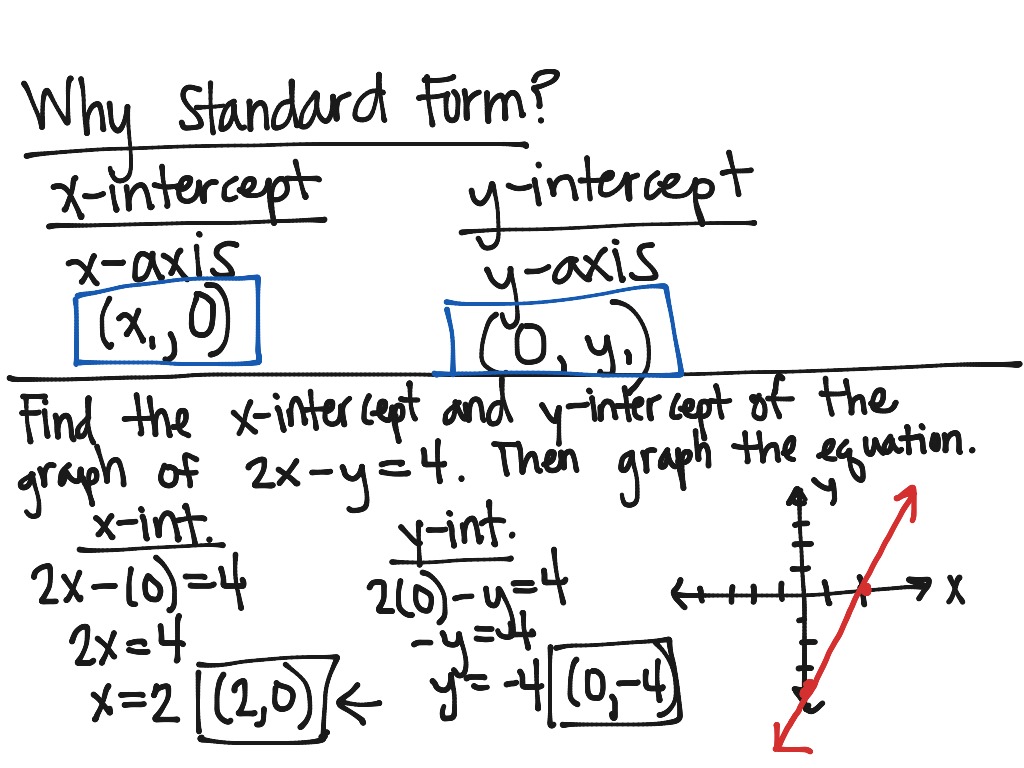
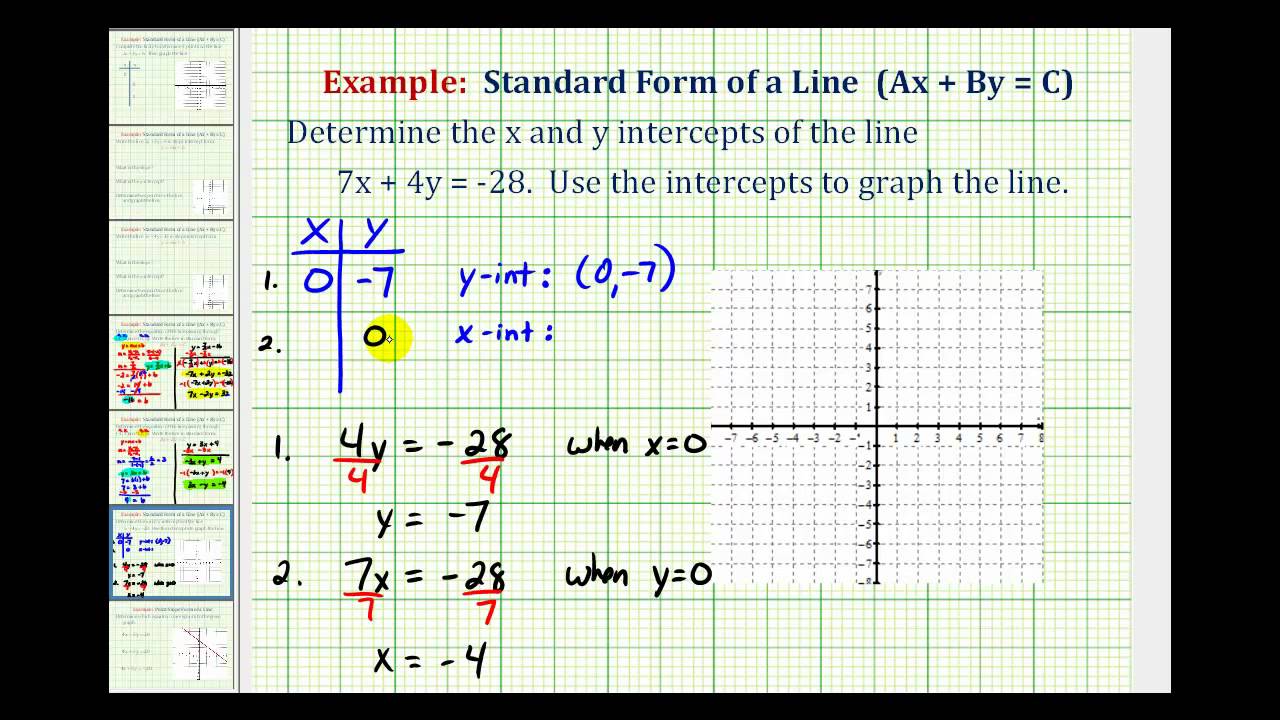
How To Write A Linear Equation In Standard Form – How To Write A Linear Equation In Standard Form
| Delightful to help my personal website, in this moment I’m going to demonstrate with regards to How To Delete Instagram Account. Now, here is the 1st image:

How about picture earlier mentioned? will be that will remarkable???. if you believe and so, I’l d teach you a number of graphic again down below:
So, if you would like secure the outstanding photos related to (How To Write A Linear Equation In Standard Form), press save button to download these pictures for your laptop. These are prepared for download, if you like and want to take it, just click save symbol in the article, and it’ll be instantly saved to your laptop computer.} Finally if you’d like to find unique and the recent image related with (How To Write A Linear Equation In Standard Form), please follow us on google plus or book mark the site, we try our best to offer you regular update with fresh and new pics. We do hope you like keeping here. For some up-dates and recent information about (How To Write A Linear Equation In Standard Form) graphics, please kindly follow us on twitter, path, Instagram and google plus, or you mark this page on bookmark section, We attempt to provide you with up-date periodically with fresh and new graphics, love your surfing, and find the right for you.
Here you are at our website, contentabove (How To Write A Linear Equation In Standard Form) published . At this time we are excited to declare that we have discovered a veryinteresting topicto be pointed out, namely (How To Write A Linear Equation In Standard Form) Many people trying to find info about(How To Write A Linear Equation In Standard Form) and of course one of them is you, is not it?