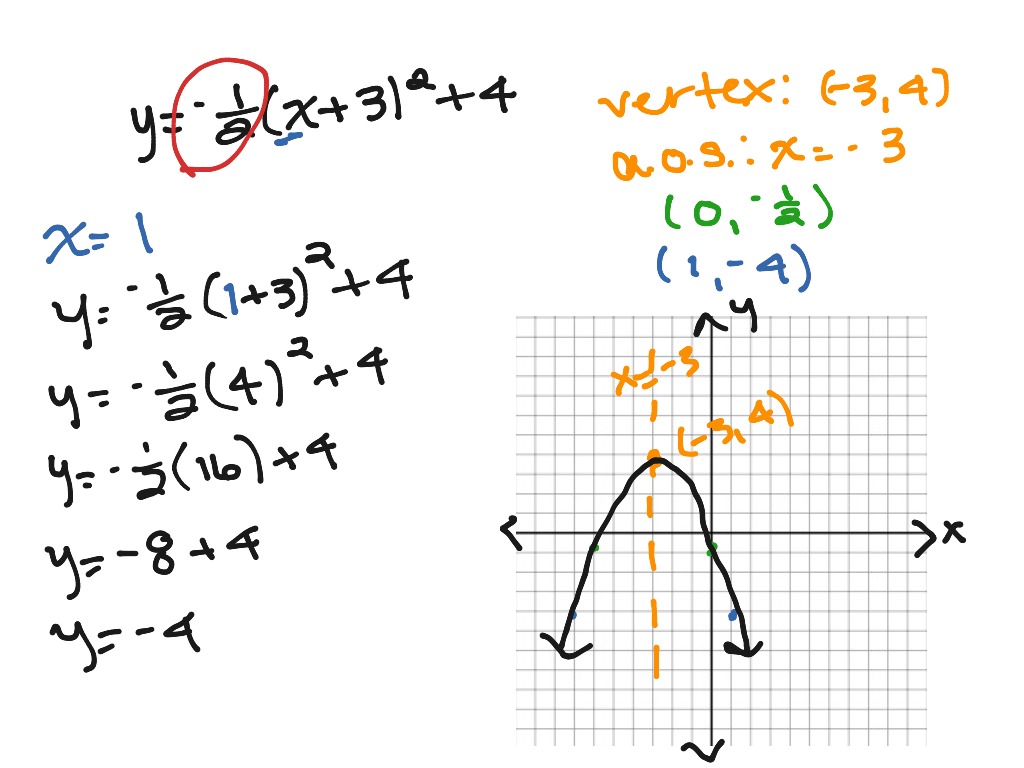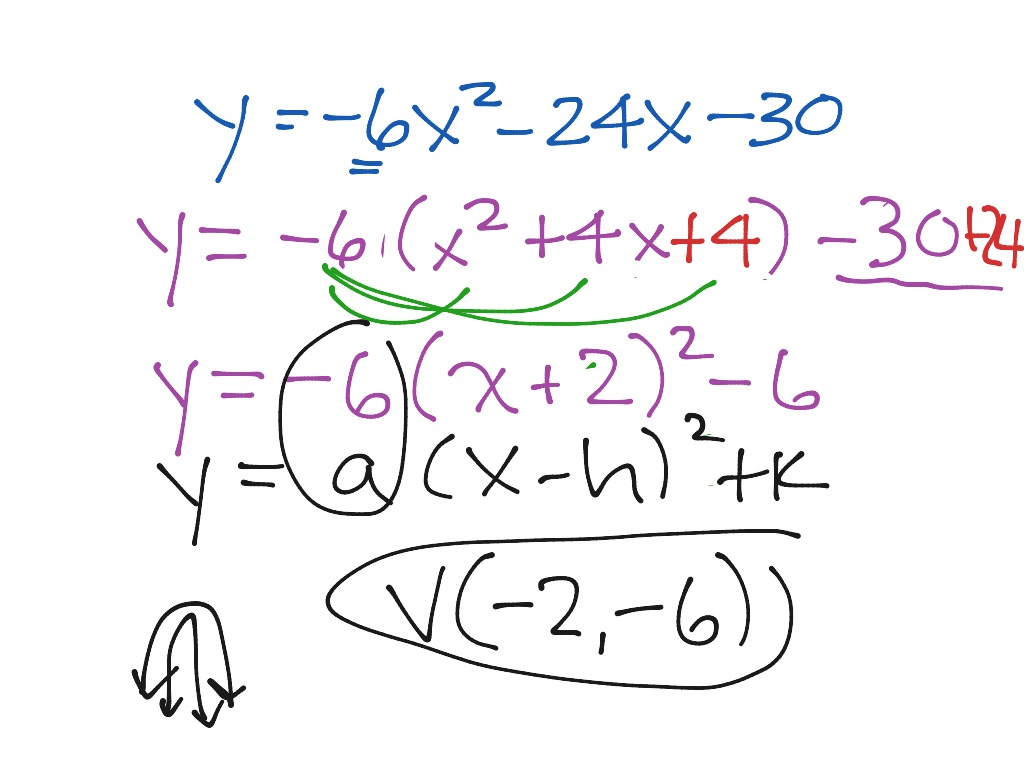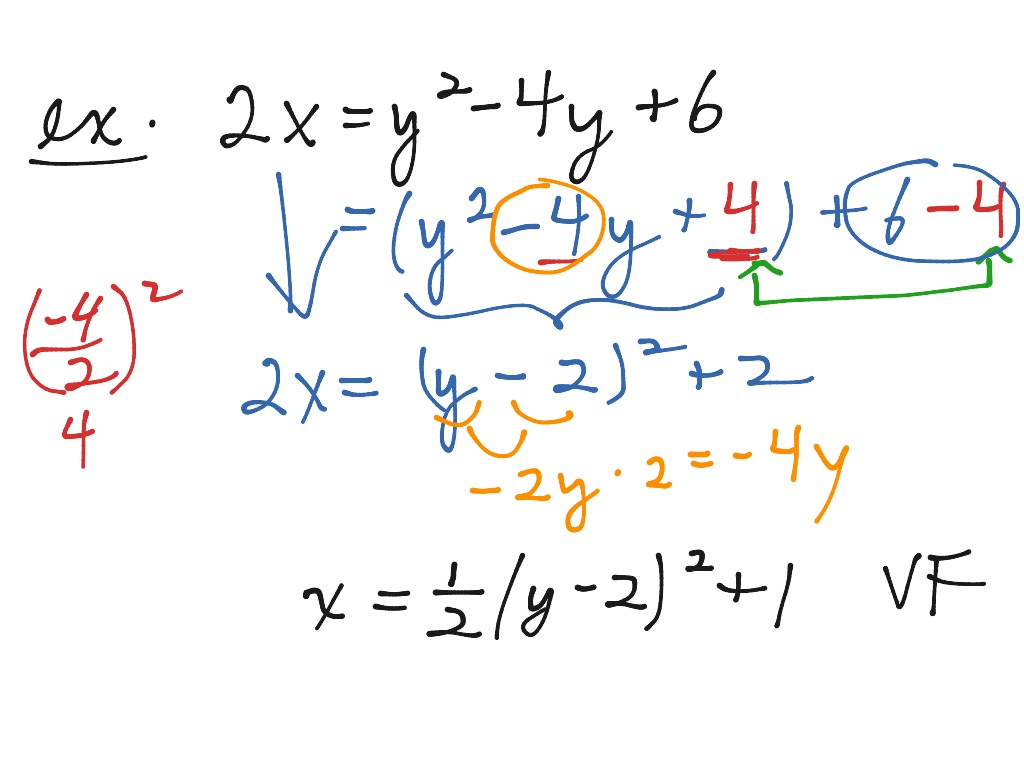In these addendum we’ll see how Prolog can be acclimated to break assorted combinatorial problems.

Three integers ((a, b, c)) anatomy a Pythagorean amateur if (a^2 b^2 = c^2). Here’s a Prolog functions that tests for Pythagorean triples:
For example:
We can use affiliate to accomplish solutions like this:
And actuality are the results:
This appearance of algorithm is sometimes referred to as accomplish and test. We accomplish a applicant solution, and again analysis it to actuate if it is valid.
Four altered Pythagorean triples are calculated. However, (3, 4, 5) and (4, 3, 5) are about the same, as are (6, 8, 10) and (8, 6, 10). So lets crave that the triples be in order:
The after-effects are little easier to read:
Of course, a limitation of these two functions is that the ethics for A, B, and C are belted to the numbers from 1 to 10. One way to fix that is as follows:
between(Lo, Hi, N) is a accepted action in SWI-Prolog that can accomplish integers from Lo to Hi (inclusive). For example:
Many programmers are afflicted by the brevity and accuracy of these sorts of Prolog programs. But it’s account acquainted that we can apparatus this aforementioned appearance of accomplish and analysis accurately in added languages. For instance, in Python we could address this:
While backtracking is not a congenital allotment of Python as in Prolog, the breeze of ascendancy all-overs about in the aforementioned way due to how and back loops terminate. Note that back the affairs is at the band if is_triple(a, b, c), again there are four places the breeze of ascendancy could jump to next.
Go is similar:

If you abolish all the angle and squint, it looks a little afterpiece to Prolog version:
All of these examples do the simplest anatomy of backtracking. For example, back they’ve angled through all ethics of c, they jump up to the b for-loop to get the abutting bulk of b. It’s never the case that the jump from c to a. This is a limitation, back in some problems it ability be (vastly) added able to backtrack to some added value.
The non-Prolog functions are not absolutely the aforementioned as the Prolog one because Prolog lets you stop afterwards you get any solution, while the added functions run to completion. However, you could simulate Prolog application generators in Python, or goroutines in Go.
Suppose we appetite to accomplish a account of all bit strings of breadth n. One way to do this relies on this actual baby ability base:
This says that 0 and 1 are bits.
To accomplish all bit strings of breadth 3, we can do this:
Lets trace this to accept how it works. Back the concern begins, A is assigned the bulk 0, B is assigned the bulk 0, and again C is assigned the bulk 0. This is a accurate assignment, and so we accept the aboriginal bit string: [0, 0, 0]. Back the user access ;, Prolog backtracks to C, which agency it unassigns C and again tries to acquisition addition bulk that satisfies C. It does: it finds that C could be 1. And so we accept the additional bit string: [0, 0, 1]. Prolog backtracks to C, unassigns it, and discovers that there are no added ethics that it can accredit to C. So now it backtracks to B, and unassigns B. It tries to acquisition a altered appointment to B, and ends up allotment 1 to B. Now it tries to acquisition a bulk for C. The aboriginal bulk it finds is 0, and so C gets assigned that. This gives the third bit string: [0, 1, 0]. Backtracking and continues in this appearance until all bit strings accept been generated.
While this is a simple way to accomplish bit strings in Prolog, it would be added acceptable to accept a action that calculates all bit strings of breadth N, e.g.:
nbits is a little bit catchy to address for new Prolog programmers, but it is able-bodied account the accomplishment to understand:
Study this function: accept every line!
Sudoku puzzles are a accepted cardinal addle that about-face out to be calmly representable in Prolog. Typically, they are played on a 9-by-9 filigree of cells, area the ambition is to put the numbers 1 to 9 into anniversary corpuscle such that:
Sudoku puzzles alpha with some numbers already abounding in, and then, through a action of accurate deduction, you try to ample in all the added numbers. It’s accessible that some puzzles ability accept added than one solution.

A four-by-four Sudoku addle is the aforementioned idea, except it is played on a 4-by-4 filigree instead of a 9-by-9, e.g.:
Each row and cavalcade charge be a about-face of the numbers 1 to 4. Also, the 4 2-by-2 sub-squares charge additionally be permutations of 1 to 4.
Here’s how we could break this addle in Prolog:
The congenital action about-face generates permutations of the associates of a list, e.g.:
We can accomplish the achievement nicer like this:
To run it, accumulation a starting 4-by-4 Sudoku grid:
Solving the 4-by-4 Sudoku addle is so aboveboard that it is accustomed to try the aforementioned access with the abounding 9-by-9 adaptation (or alike bigger!). However, while it will assignment in principle, there are so abounding possibilities to chase through in the 9-by-9 adaptation that the affairs won’t accomplishment in a reasonable bulk of time.
To see why, aboriginal apprehension that the affairs does not use any ability specific to Sudoku. It solves the addle by authentic animal force: it generates all accessible permutations and tests which ones amuse the constraints.
We can get a asperous appraisal of the cardinal of altered 9-by-9 Sudoku boards as follows. Anniversary row has (9! = 362880) accessible permutations, and back there are 9 rows there are (9!^9 approx 1.1 times 10^{51}) possibilities for this generate-and-test affairs to try.
Assuming we could accomplish a abundance ((10^{12})) permutations per second, it would booty on the adjustment of (10^{39}) abnormal to solve, which is about (3 times 10^{29}) centuries.
People can acutely break 9-by-9 puzzles abundant added bound than that. They do it by application ability specific to Sudoku to added calmly amount out numbers. Our affairs has no ability about Sudoku added than what counts as a solution. With added work, it is accessible to add added ability to accomplish it faster, but we don’t do that here.
The SEND MORE MONEY addle is a archetypal cryptarithmetic addle that can be apparent neatly in Prolog. The addle asks you to alter belletrist with numbers that makes this blueprint true: SEND MORE = MONEY. Anniversary letter stands for a distinct digit, 0 to 9, and altered belletrist are altered digits (so, for example, S and E can’t be the same). Also, S and M can’t be 0 because numbers don’t alpha with 0.

There are a brace of means to break this botheration in Prolog. One way is like this:
This takes a few abnormal to run on a archetypal desktop computer, and it finds the one altered solution:
Importantly, as anon as ethics are assigned to variables, we accomplish the dis- adequation constraints so that abortion will appear as anon as possible. It would run abundant added boring if, say, you put all the = constraints in one accumulation at the bottom.
An alike added able access is to actor how bodies do addition:
Again, we interleave constraints with calls to amid for efficiency. The variables C1, C2, and C3 are the backpack ethics of the additions of the alone digits.
The all_diff action succeeds aloof back all the elements on the account anesthetized to it are different, e.g.:
Here’s an implementation:
What’s nice about this accepted access is that the affairs is about aloof a account of the constraints on the variables. We again let Prolog do the assignment of award acceptable values.
While this access is abundant in theory, in convenance it about requires a lot of added problem-specific cipher to accomplish such programs run efficiently.
Map appearance is a archetypal computational problem. By a map is meant a graph, i.e. a set of vertices affiliated by edges.
In a map appearance problem, the assignment is to accredit to anniversary acme a blush such that no two edges affiliated by an bend allotment the aforementioned color. In general, this is computationally arduous problem, i.e. free whether or not a blueprint can be 3-colored is NP-complete.
One way to represent a map 3-coloring botheration in Prolog is as follows:

While this is a nice archetype of a Prolog program, it is not the best able way to break a appearance problem. For ample maps, it is far too inefficient: if Prolog did smarter backtracking, or acclimated heuristics specific to map coloring, it could do abundant better.
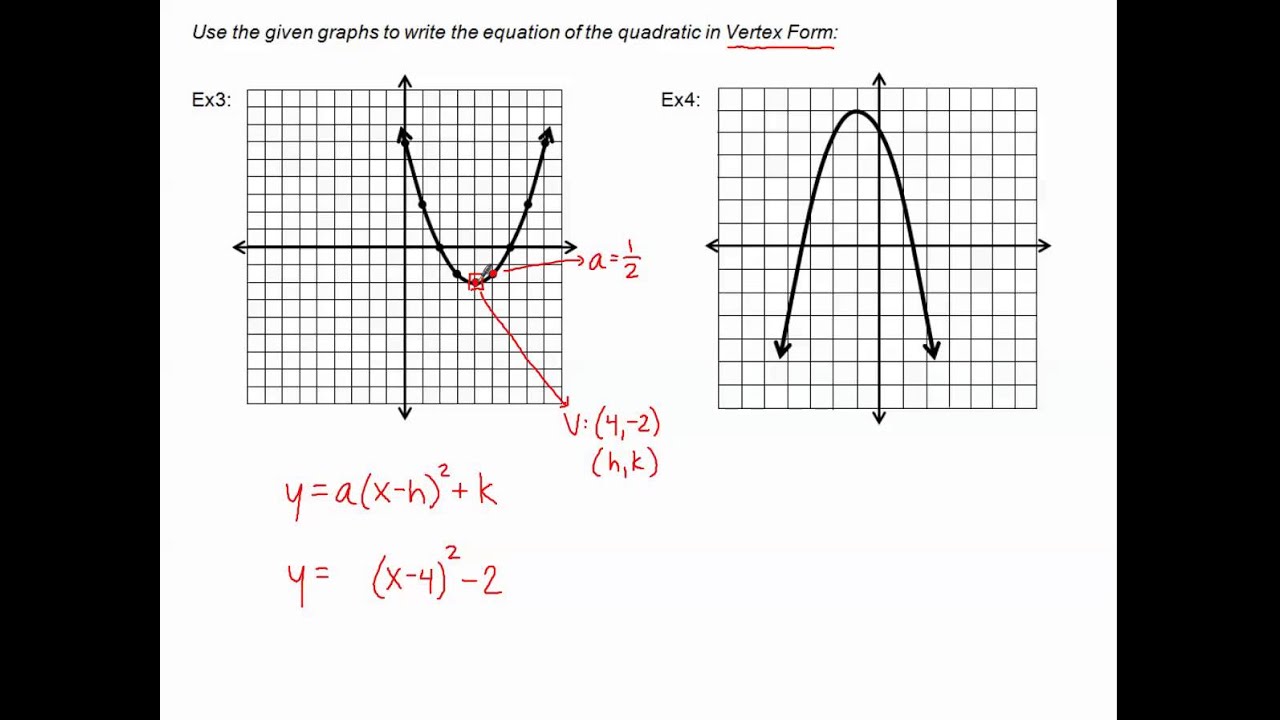
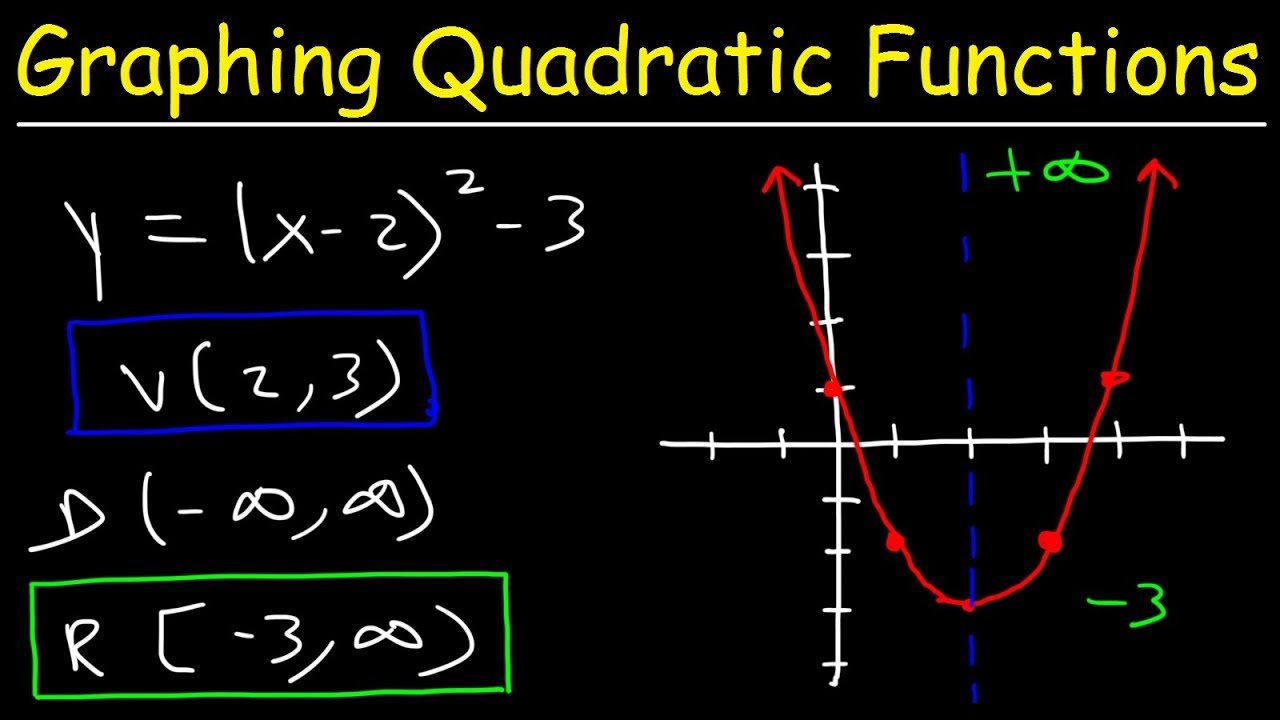
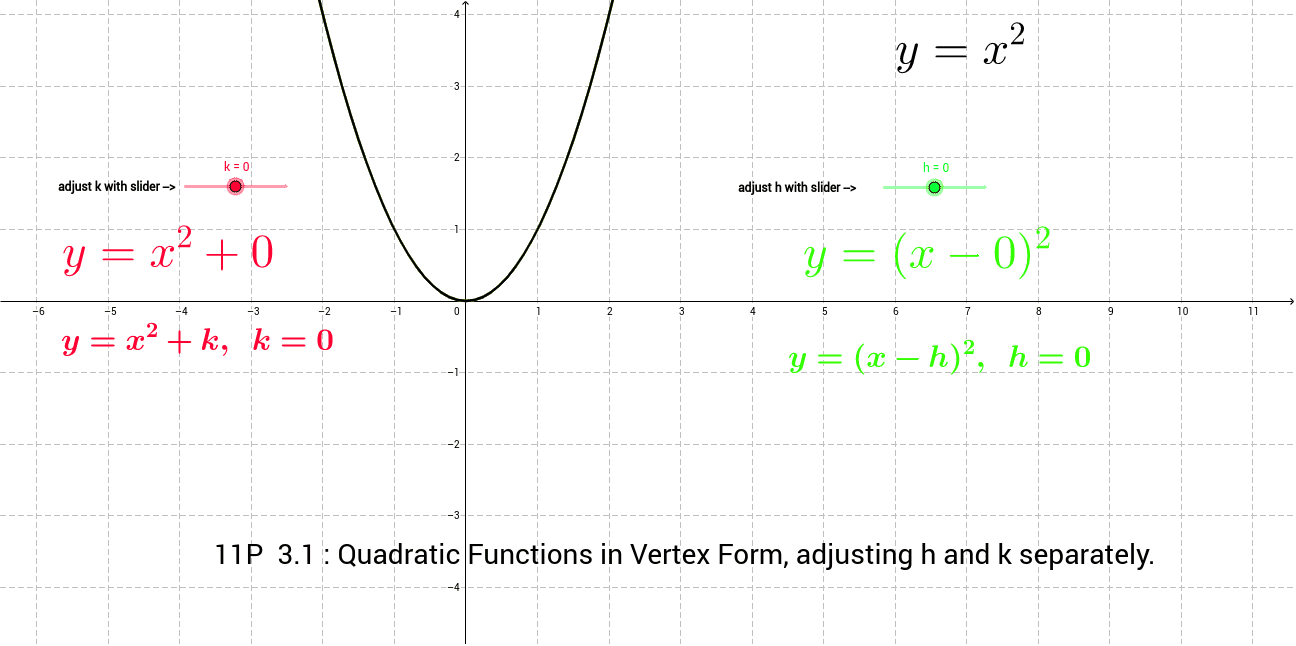
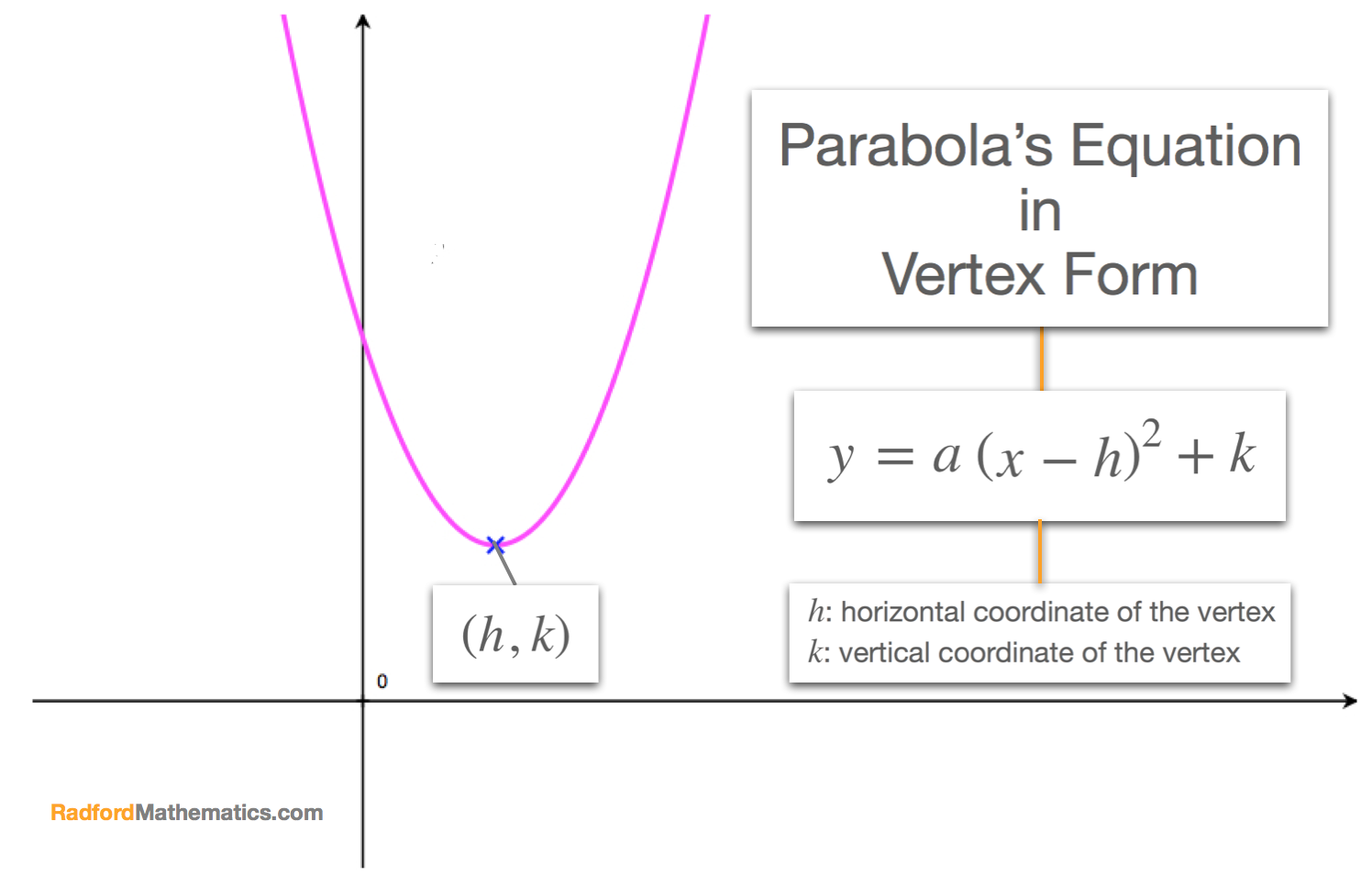
How To Write A Function In Vertex Form – How To Write A Function In Vertex Form
| Encouraged to help the website, in this period We’ll demonstrate concerning How To Factory Reset Dell Laptop. And now, this is the initial photograph:
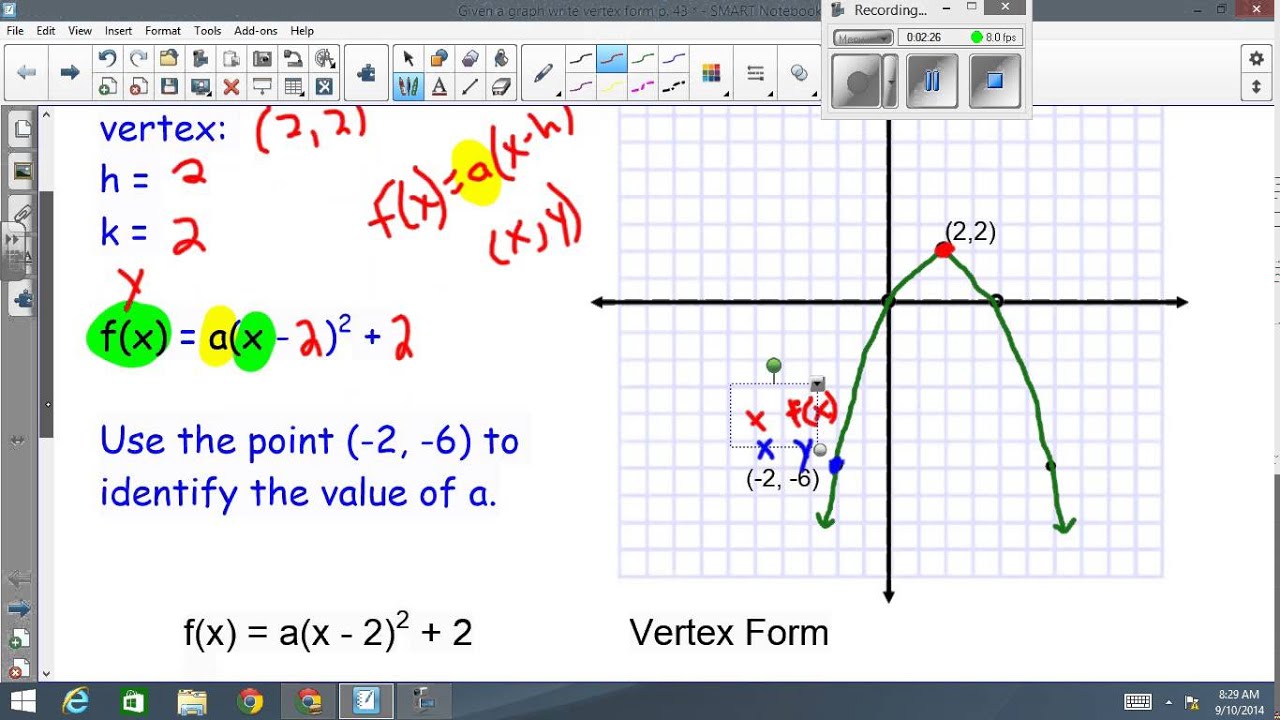
What about picture earlier mentioned? will be in which awesome???. if you think therefore, I’l m provide you with several image all over again beneath:
So, if you’d like to have the incredible images regarding (How To Write A Function In Vertex Form), just click save button to download the shots for your personal pc. These are prepared for save, if you’d prefer and want to take it, just click save logo on the page, and it will be instantly downloaded in your home computer.} As a final point if you need to have unique and recent graphic related with (How To Write A Function In Vertex Form), please follow us on google plus or bookmark this blog, we attempt our best to give you regular up grade with fresh and new pics. We do hope you like keeping here. For most upgrades and recent information about (How To Write A Function In Vertex Form) pictures, please kindly follow us on twitter, path, Instagram and google plus, or you mark this page on book mark section, We attempt to present you update regularly with all new and fresh pics, enjoy your browsing, and find the ideal for you.
Here you are at our site, contentabove (How To Write A Function In Vertex Form) published . Nowadays we are pleased to declare that we have discovered an awfullyinteresting topicto be reviewed, namely (How To Write A Function In Vertex Form) Lots of people searching for specifics of(How To Write A Function In Vertex Form) and of course one of them is you, is not it?