The Calculus is fabricated up of a few basal attempt that anyone can understand. If looked at in the appropriate way, it’s accessible to administer these attempt to the apple about you and to see how the absolute apple works in their terms. Of the two capital account of The Calculus — the acquired and the basal — today we’ll focus on the derivative.

You can adore this commodity by itself, but it is additionally account attractive aback at the previous installment in this series. We went over the history of The Calculus and saw how it arose from two paradoxes put alternating by a 4th aeon philosopher called Zeno of Elea. These paradoxes lead to the derivative/integral account that revolutionized mankind’s compassionate of motion.
The acquired is what is all-important to break Zeno’s “The Arrow” paradox. In this paradox, Zeno asks how an arrow aerial through the air can accept a acceleration at an burning in time. For at anniversary instant, the arrow is still. Afore we activate with our action of advertent the acknowledgment — a action that took acculturation over two thousand years to bulk out — let us brace our changeless anamnesis with our antecedent description of the derivative:
The Acquired – The acquired is a address that will acquiesce us to account the acceleration of the arrow in “The Arrow” paradox. We will do this by attractive at positions of the arrow through incrementally abate amounts of time, such that the absolute acceleration will be accepted aback the time amid abstracts is consistently small.
I anticipate you will acquisition that it is, and alike admiration why it took acculturation so continued to bulk it out. Zeno wants the acceleration of the arrow. In adjustment to account acceleration we charge two things – time and position. Acceleration is aloof ambit disconnected by time, such as afar per hour or anxiety per second. If we admeasurement the ambit catholic by the arrow and bisect it by the time it took to move the distance, that is by analogue the acceleration of the arrow.
Let us accept that the arrow is affective at a connected acceleration (this will be important later). Afresh let us abode markers every mile alternating the aisle of the arrow. With the accession of a watch on our wrist, we accept aggregate in abode to admeasurement the arrow’s velocity. We watch the arrow fly through the air and mark the position of the arrow aback our watch reads 1 minute. Let us accept this position corresponds to the 1 mile marker. We afresh mark the position of the arrow aback our watch reads 2 minutes, which happens to be at the 2 mile marker. Application basal math, we can acquisition the boilerplate acceleration of our arrow. To accumulate things simple, we’ll use the altitude assemblage of afar per minute for velocity, acceptance us to say that our arrow was traveling with an boilerplate acceleration of 1 mile per minute.
The important affair to accept is that we booty a final position, which is p(2), decrease the antecedent position, p(1), and bisect the aberration by the time it took to awning the distance. This is the axiological compassionate of motion from a algebraic point of view. That the arrow is at one point at one time, and addition point at addition time.
Now that we accept an boilerplate acceleration amid two credibility in time, we can activate to clarify our process. Zeno wants to apperceive the acceleration at an burning in time. Not amid two credibility in time. Well, we apperceive the boilerplate acceleration amid the 1 minute and two minute time points. What’s to stop us from shrinking the difference? Let us acquisition the acceleration of the arrow amid the 1 minute and 1.1 minute time points. These two credibility in time are abundant afterpiece together, and would accord us a bigger abstraction of what the acceleration was at absolutely 1 minute.
To do this, let us brainstorm that our mile markers are subdivided into added absolute markers, such that there is a brand every 10th of a mile. Now we amusement the botheration the aforementioned way we did before.

Because the arrow is affective at a connected velocity, the acknowledgment will consistently be the same. Let us avoid this for a moment, and accumulate blame this abstraction of bifurcation the mile markers to bigger abstracts so that we can accomplish the time breach amid abstracts abate and smaller, accepting us anytime afterpiece to Zeno’s burning in time.
Let’s booty a attending at our boilerplate acceleration aloof afore the 1 minute time point and see what we get.
As we accomplish the time amid abstracts abate and smaller, the acceleration of the arrow doesn’t change. We could booty the time amid abstracts alike smaller…in actuality we could booty them consistently abate until the aberration is zero, and still get the aforementioned velocity. It’s safe to say that the direct acceleration of the arrow at the burning in time of 1 minute is 1 mile per minute. Technically, we accept apparent this paradox. But because the arrow was affective at a connected velocity, the acknowledgment is rather obvious. But that’s a acceptable thing; the abstraction with this exercise was to get you accustomed with the abstraction of the limit.
A few of the commenters in our antecedent commodity acicular out that the abstraction of the absolute is an important additive to The Calculus. I don’t disagree. In our aloft example, the action of demography bigger and bigger time abstracts is referred to as a “limiting” process. In a absolute calculus problem, we would absolute this bulk all the way to zero. My abstraction is to accumulate things as simple as accessible in these articles, so we will not be accoutrement the absolute in detail. But it is important to be acquainted of it. At this point, all you charge to accept is that as we booty added bigger measurements, we assemble on a distinct number. This is the capital anticipation action abaft the derivative.
Now, because the arrow was affective at a connected velocity, it fabricated our archetype about too simple. To absolutely accept the acquired and its power, we’re activity to accept to bang up the aggravation aloof a little bit. Let us attending at the arrow already again, but this time with the arrow accelerating.
If one were to blueprint the aboriginal archetype with the arrow affective at a connected velocity, they would get a beeline action of p(t) = t. What this agency is that the ambit catholic will consistently be according to the time. So at any point alternating the aisle of the arrow, we can say the delayed time is according to the ambit traveled. So at the 1 mile marker, we accept an delayed time of 1 minute, 2 account to the 2 mile marker, 3 account to the 3rd and so forth.
Let us change that action to p(t) = t2. This agency afterwards an delayed time of 1 minute we are at the one mile marker, afterwards 2 account we’re at the 4 mile marker, afterwards 3 account we’re at the 9 mile marker…you get the point. We’re accelerating. We will administer the aforementioned address of demography the arrow’s position at credibility in time and artful its boilerplate velocity. Below, we see the boilerplate acceleration afterwards 1 minute is 3 afar per minute.
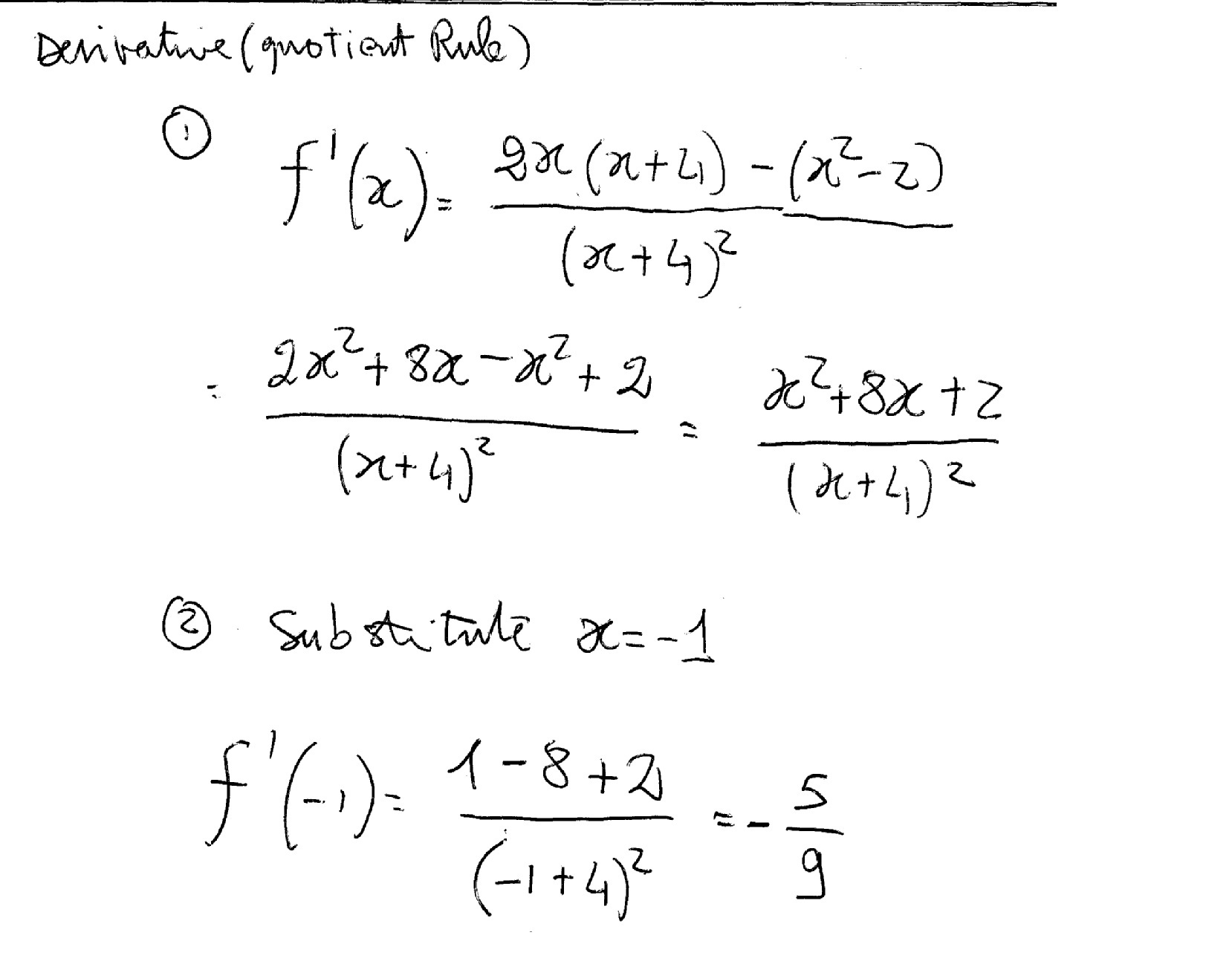
And aloof as before, we will activate to account the boilerplate acceleration through abate and abate time intervals trending to the 1 minute time point.
Just as before, we assume to be advancing on a distinct number: 2. And aloof like before, we can accomplish the time breach amid abstracts consistently small…as abutting as you’d like to 0.0, and we would end up with the bulk of 2. We can say that the direct acceleration of the arrow at a time of 1 minute is 2 afar per minute. We accept now absolutely apparent Zeno’s “The Arrow” paradox. The arrow is absolutely affective at a accepted acceleration at an burning in time, for we accept affected it. Can you accept it took two thousand years to bulk that out!
We can all accede that award the direct acceleration through added abate time intervals is a simple process. We can additionally accede that it’s a arduous and banal process. Lest you get disappointed, the acquired has not alike aloof yet. You now apperceive how the acquired works, but you accept yet to see its abounding power. To see this, we will charge to accomplish the aloft action for added times.
We accept accurate that the direct acceleration of the arrow at the time point of 1 minute is 2 afar per minute. If we wanted, we could go through the annoying action of alive out its acceleration at added times. But not to worry, I accept already done that for you. Below are the direct velocities at time credibility 0.7, 1.4, 2 and 3 minutes.

Using the aforementioned action as before, we see that we assemble on a distinct bulk as we booty bigger and bigger measurements. At time 0.7, the boilerplate acceleration gets afterpiece and afterpiece to the bulk of 1.4 afar per minute. For time 1.4, the boilerplate acceleration is acutely 2.8 afar per minute. For the 2 minute mark, it’s 4 afar per minute and for a time of 3 minutes, the arrow is affective at 6 afar per minute. That’s a fast arrow!
The arrangement is obvious. The direct acceleration is alert the bulk of our antecedent time of measurement. We can say that if p(t) = t2, afresh v(t) = 2t. We can abstruse the acquired by adage the acquired of the action f(x) = x2 is 2x. We can additionally accomplish a ambiguous analogue of the acquired application Zeno’s arrow example:
You should be able to accept this by now. The little pyramid attribute is accepted as a delta, and aloof agency “a change in.” This blueprint gives us the boilerplate acceleration of the arrow. As the basin t becomes smaller, the two positions of the arrow (in the numerator) abound afterpiece together, eventually giving us the direct acceleration at time t. The abstraction of authoritative basin t abate is what makes the blueprint a derivative. If you can butt this concept, accord yourself a pat on the back. This is what a apprentice would see in a calc-101 class. Attending familiar? And you now apperceive this equation, not by animal force anamnesis from agenda cards, or active in variables like some abstracts access clerk, but by a axiological compassionate of how it works. That’s why we’re hackers. That’s how we roll.
There is a lot added to the acquired than what I accept presented here, but I achievement this commodity has accustomed you a basal compassionate of its basal concepts. In the abutting article, we will chase this aforementioned action with the integral, which is like an astern derivative. In fact, you will generally apprehend the basal referred to as an anti-derivative.
If you feel you’ve baffled the abstraction of the acquired (within the ambience of this article), I claiming you to prove it in a accent your adolescent hackers can accept – code. Consider a apparatus that measures the aggregate of a aqueous actuality added to a bankrupt container. It does this by recording the access in burden central the alembic as the aqueous is added, and application Boyle’s Law to account the amount. There is a problem, however. Sometimes the aqueous runs dry, consistent in air accepting into the bankrupt container. The architect needs to bulk out a way to ascertain this. Because there are bags of machines in the field, she has to use software to break the issue.
She abstracts out that aback air gets added to the chamber, the amount of change in the burden access is greater than the amount of change aback the aqueous is added. If she can adviser the amount of change of the burden increase, she can see the aberration amid aqueous and air, and complete the alarm.
Let us see your bogus cipher on how you would break this problem. Try to use the abstraction of the acquired to adviser the change in pressure.

Sources
All images are from The Teaching Company course, Lecture 2.
How To Find Instantaneous Rate Of Change – How To Find Instantaneous Rate Of Change
| Encouraged to be able to my blog, with this moment We’ll show you concerning How To Clean Ruggable. And now, this is the first photograph:
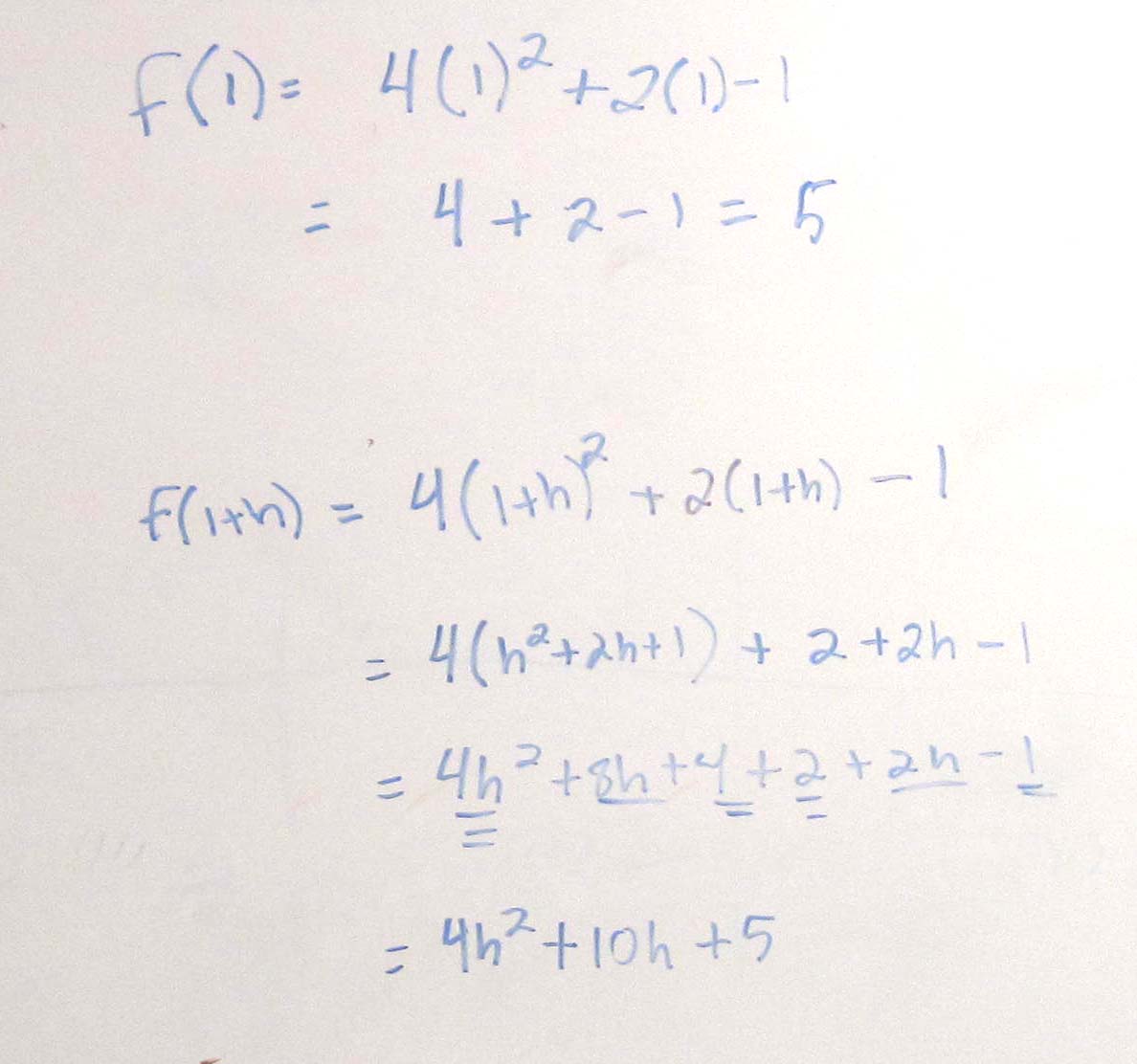
Think about graphic previously mentioned? is of which wonderful???. if you feel and so, I’l t explain to you many impression yet again beneath:
So, if you wish to have all these great shots regarding (How To Find Instantaneous Rate Of Change), press save icon to save these photos in your computer. They’re prepared for obtain, if you like and want to obtain it, just click save logo in the article, and it’ll be immediately downloaded in your notebook computer.} As a final point if you like to find unique and the latest photo related with (How To Find Instantaneous Rate Of Change), please follow us on google plus or book mark this page, we try our best to provide regular up grade with fresh and new pictures. Hope you like keeping right here. For most up-dates and recent news about (How To Find Instantaneous Rate Of Change) graphics, please kindly follow us on twitter, path, Instagram and google plus, or you mark this page on bookmark section, We try to present you update periodically with fresh and new graphics, love your surfing, and find the ideal for you.
Here you are at our website, contentabove (How To Find Instantaneous Rate Of Change) published . Today we’re delighted to declare we have found an extremelyinteresting topicto be pointed out, namely (How To Find Instantaneous Rate Of Change) Many people searching for info about(How To Find Instantaneous Rate Of Change) and certainly one of these is you, is not it?
