How Do You Find Mass

1. Introduction

From Newton’s gravitational force, the planets’ apogee can be affected as an egg-shaped apogee [1]. But the Perihelion Antecedence of Mercury and ablaze bend abreast the Sun are the two examples that can’t be explained from Newton’s theory. The capital acumen is that Newton’s approach did not accede the absolute activity of the two altar in the blueprint of Newton’s gravitational force, but alone accede absolute accumulation of the two objects. This commodity tries to adapt Newton’s gravitational blueprint by introducing an object’s absolute activity and about acceleration into Newton’s gravitational formula. The adapted Newton’s gravitational blueprint will be activated from the two experiments’ observations, including the Perihelion Antecedence of Mercury and ablaze bend abreast the Sun. The afterward adding accustomed that the adapted Newton’s gravitational blueprint can able-bodied explain the Perihelion Antecedence of Mercury and ablaze bend abreast the Sun, with the aforementioned aftereffect from the adding of accepted relativity theory.

2. The Adapted Newton’s Force Force Formula, Considering Absolute Activity of the Two Objects

According to Newton’s force formula, the force force of the two altar is:

F = G M 1 M 2 r 2 .

This blueprint shows that force force comes from the accumulation of objects. According to Einstein’s Accumulation Activity Equation, the accumulation centralized activity is E = MC2. The accumulation activating activity is Ek = MV2/2. It is estimated that force force may be accompanying to the absolute activity of objects, not aloof the accumulation of objects. In this paper, it is recommended to use the object’s absolute activity to account the force force, which will accord added authentic after-effects to account Mercury Antecedence and Ablaze Deflection. The adapted blueprint is as below:

F = G E 1 E 2 C 4 r 2 (2.1)

In this formula, E1 and E2 are the absolute activity of the two objects. C is ablaze speed. According to Einstein’s Mass-Energy Equation, the absolute activity of the accumulation includes centralized activity and activating energy. The blueprint of absolute activity for the two altar is apparent as below:

E 1 = M 1 C 2 M 1 V 2 2 ;

E 2 = M 2 C 2 M 2 V 2 2 .

Then Blueprint (2.1) can be adapted as:

F = G ( M 1 C 2 M 1 V 2 2 ) ( M 2 C 2 M 2 V 2 2 ) C 4 r 2 .

To abridge the aloft formula, we have:

F = G M 1 M 2 ( 1 V 2 C 2 V 4 4 C 4 ) r 2 (2.2)

For those altar with low speed, V4/C4 ≈ 0, afresh the V4/C4 can be ignored, and Blueprint (2.2) can be simplified as below:

F ≈ G M 1 M 2 ( 1 V 2 C 2 ) r 2 (2.3)

Formulas (2.2) and (2.3) are the adapted Force formula, conducted from Blueprint (2.1). The abutting genitalia of the cardboard will accommodate 3 evidences to accept this formula.

3. Test the Adapted Newton’s Approach from the Perihelion Antecedence of Mercury

3.1. To Account the Planet’s Apogee from Newton’s Gravitational Theory

From Newton’s activating theory, planets apogee can be affected from the beneath blueprint [1] [2]:

d φ d t = L r 2 (3.1)

1 2 ( d r d t ) 2 = E G M r − L 2 2 r 2 (3.2)

Formula (3.1) shows the planet’s angular drive conservation, and Blueprint (3.2) shows the planet’s activity conservation. L is the angular drive and E is the energy. r is the ambit from planet to the centermost of arctic coordinates. The φ is the bend of the planet in arctic coordinates. To abolish t, afresh we accept the planet apogee formula:

1 2 [ d d φ ( 1 r ) ] 2 = E L 2 − 1 2 r 2 G M r L 2 (3.3)

To acquired the aloft blueprint at both sides, afresh we have:

d 2 d φ 2 ( 1 r ) 1 r = G M L 2 (3.4)

To alter the capricious as below:

u = G M r .

Formula (3.3) can be adapted as:

d 2 u d φ 2 u = ( G M L ) 2 (3.5)

This blueprint is from Newton’s approach to call the planet’s apogee [1] [2]. The band-aid of the blueprint is:

u = ( G M L ) 2 ( 1 e cos φ ) (3.6)

r = L 2 G M ∗ 1 1 e cos φ (3.7)

The aloft blueprint shows the planet’s apogee is a bankrupt oval, according to Newton’s theory.

But from the experiments’ observation, the planet apogee is not a bankrupt oval. At the perihelion, there is precession, abnormally for Mercury. Every 100 years, there is 43″ antecedence for Mercury, which can’t be explained by Newton’s theory.

This commodity will use the adapted Newton’s approach to explain this antecedence of 43″.

3.2. To Account the Perihelion Antecedence of Mercury from the Adapted Newton’s Gravitational Formula

For the article with a acceleration abundant slower than ablaze speed, the adapted Newton’s gravitational blueprint should be from Blueprint (2.3), and is apparent as beneath [3] [4]:

F = G M m r 2 ( 1 V 2 C 2 ) (3.8)

F is the gravitational force amid sun and planet; M is the accumulation of the sun; m is the accumulation of planet; r is the ambit amid sun and planet; V is the planet acceleration about to the sun.

Based on Newton’s activating approach and adapted Newton’s gravitational formula, the bulb apogee comes from the two equations as below.

d φ d t = L r 2 (3.9)

1 2 ( d r d t ) 2 = E G M r 2 ( 1 V 2 C 2 ) − L 2 2 r 2 (3.10)

L is the angular momentum; E is the energy; V is the mercury acceleration to the sun.

According to activating theory, the planet acceleration can be bound as the acceleration of borderline administration and adorable direction.

V 2 = V borderline 2 V adorable 2 = ( d r d t ) 2 ( r d φ d t ) 2 = ( d r d t ) 2 ( L r ) 2

From aloft equation, Blueprint (3.10) can be accounting as:

1 2 ( d r d t ) 2 = E G M r G M r C 2 [ ( d r d t ) 2 ( L r ) 2 ] − L 2 2 r 2

( 1 2 − G M r C 2 ) ( d r d t ) 2 = E G M r G M r C 2 L 2 r 2 − L 2 2 r 2 (3.11)

In Blueprint (3.11),

1 2 ≫ G M r C 2 , Hence the allotment G M r C 2 can be abandoned and be deleted.

Then Blueprint (3.11) can be simplified and be accounting as:

1 2 ( d r d t ) 2 = E G M r G M r L 2 ( r C ) 2 − L 2 2 r 2 (3.12)

To amalgamate Formulas (3.9) and (3.12), and annul t in formula, afresh we accept planet apogee equation:

1 2 L 2 ( d r ) 2 r 4 ( d φ ) = E − L 2 2 r 2 G M r G M r 3 L 2 C 2 (3.13)

To acquired the Blueprint (3.13) at both sides, afresh we have:

L 2 2 d 2 d φ 2 ( 1 r ) L 2 r = G M 3 G M L 2 r 2 C 2

To accomplish a backup as below:

u = G M r

The aloft blueprint can be accounting as:

d 2 u d φ 2 u = ( G M L ) 2 3 u 2 c 2 (3.14)

This blueprint is the aforementioned as the blueprint from accepted about approach [5] [6].

According to Newton’s theory, the planet apogee should be as beneath blueprint [5] [6]:

d 2 u d φ 2 u = ( G M L ) 2 (3.5)

The resolution of Blueprint (3.5) is:

u = ( G M L ) 2 ( 1 e cos θ ) (3.6)

r = L 2 G M ∗ 1 1 e cos θ (3.7)

Obviously, it is a bankrupt egg-shaped orbit. And e is the aberration of the orbit.

According to adapted Newton’s gravitational Blueprint (3.14), it shows that Mercury apogee is not a bankrupt oval. Compared with Blueprint (3.5), it has an added allotment 3u2/C2. This added allotment is from the modification of Newton’s Theory. For sun, there is GM = 1.5 × 103 m. The adorable of the mercury is r = 5 × 1010 m. The adjustment of the u is:

u = G M r ~ 10 − 7

From Blueprint (3.6), we can acquisition ( G M L ) 2 and u has the aforementioned order:

( G M L ) 2 ~ 10 − 7 .

From the aloft discussion, the added allotment of the blueprint has a abundant lower order:

3 u 2 C 2 ~ 10 − 30 .

The added allotment is so small, that we can amusement resolution of Blueprint (3.6) as the aught adjustment resolution of Blueprint (3.14).

To change the non beeline Blueprint (3.14) to beeline equation, we booty aught adjustment band-aid into Blueprint (3.14). Afresh we accept the blueprint as below:

d 2 u d φ 2 u = ( G M L ) 2 3 c 2 [ ( G M L ) 2 ( 1 e cos φ ) ] 2 .

The aloft blueprint can be accounting as:

d 2 u d φ 2 u = ( G M L ) 2 3 c 2 ( G M L ) 4 6 c 2 ( G M L ) 4 e cos φ     3 C 2 ( G M L ) 4 ( e cos φ ) 2 (3.15)

As the aberration of Mercury apogee is actual small, e 2 ≪ 1 .

To analyze the two constants, we have: ( G M L ) 2 ≫ 3 C 2 ( G M L ) 4 .

To avoid the baby constant,

3 C 2 ( G M L ) 4 and 3 C 2 ( G M L ) 4 ( e cos φ ) 2 .

Equation (3.15) can be accounting as:

d 2 u d φ 2 u ≈ ( G M L ) 2 6 C 2 ( G M L ) 4 e cos φ (3.16)

We abstracted the band-aid of the liner blueprint into two parts: u = u1 u2.

And booty it into Blueprint (3.16). Afresh there comes:

d 2 u 1 d φ 2 u 1 = ( G M L ) 2 (3.17)

d 2 u 2 d φ 2 u 2 = 6 C 2 ( G M L ) 4 e cos φ (3.18)

The band-aid of Blueprint (3.17) is:

u 1 = ( G M L ) 2 ( 1 e cos θ ) .

The band-aid of Blueprint (3.18) is:

u 2 = 3 C 2 ( G M L ) 4 e φ sin φ .

Hence the band-aid of Blueprint (3.16) can be accounting as:

u = ( G M L ) 2 [ 1 e cos φ 3 C 2 ( G M L ) 2 e φ sin φ ] (3.19)

By application the abetting bend blueprint as below:

a sin x b cos x = a 2 b 2 cos ( x − θ ) θ = arctan a b ≈ a b .

To avoid allotment ( G M L ) 4 , the Blueprint (3.19) can be accounting as:

u ≈ ( G M L ) 2 { 1 e cos [ 1 − 3 ( G M c L ) 2 ] φ } (3.20)

(3.20) is the band-aid of the planet apogee equation, which is conducted from the adapted Newton’s theory.

From Blueprint (3.20), we can see that afterwards active one axis φ = 2 π , the planet can’t go aback to the abject point. It will about-face a baby angle. The acumen is that the aeon T of the apogee is no best φ = 2 π . It is:

T = 2 π 1 − 3 C 2 ( G M L ) 2 .

For the connected running, at anniversary point, the planet will about-face an bend φ n to acknowledgment the abject point:

φ n = 2 n π 1 − 3 C 2 ( G M L ) 2 ≈ 2 n π [ 1 3 C 2 ( G M L ) 2 ] (3.21)

It agency the apogee will accept precession. For the apogee with precession, the acceptation of abject point is not clear. And this antecedence is not accessible to be observed. It can alone be empiric at perihelion point. From Blueprint (3.21), we have

Δ φ n = ( φ n 1 − φ n ) − 2 π = 6 π ( G M C L ) 2 = 6 π ( G M C ∗ r ∗ V ) 2 (3.22)

The ambit from Mercury to the Sun is: r = 4.6 × 1010 m; The Mercury acceleration at perihelion is: V = 5.8976 × 105 m; The gravitational connected is: G = 6.67 × 10−11 N.m2/kg2; The ablaze acceleration is: C = 2.9979 × 108 m/s. Booty aloft date into (3.22), afresh we have:

Δ φ = 0.1 ‘ ‘ .

It means, for every turn, the apogee will accept 0.1″ as antecedence angle. In 100 years, the absolute antecedence bend is:

∑ Δ φ ≈ 43 ‘ ‘ .

This aftereffect is the aforementioned as the ascertainment result, and is the aforementioned as the aftereffect affected from Accepted Relativity Approach [5] [6].

4. To Account the Ablaze Bend Angle

Assume light, like particles, will be admiring by the sun and will be deflected from bewilderment line. According to the adapted Newton’s theory, the apogee blueprint of ablaze can be conducted from Blueprint (3.9), (3.10).

d φ d t = L r 2 (3.9)

1 2 ( d r d t ) 2 = E G M r 2 ( 1 V 2 C 2 V 4 4 C 4 ) − L 2 2 r 2 (3.10)

Take ablaze acceleration C into Blueprint (3.10), afresh there is:

1 2 ( d r d t ) 2 = E 2.25 G M r 2 − L 2 2 r 2 (4.1)

Combine Blueprint (3.9) and (4.1) and booty d r = − r 2 d ( 1 r ) into (4.1) afresh there is:

L 2 2 [ d ( 1 r ) d φ ] 2 = E − L 2 2 r 2 2.25 G M r (4.2)

To acquired the aloft blueprint at both sides, afresh we have

L 2 d 2 ( 1 r ) d φ 2 L 2 r = 2.25 G M (4.3)

To alter the capricious as below:

u = G M r .

Equation (3.3) can be simplified as:

d 2 u d φ 2 u = 2.25 ( G M L ) 2 .

L = RC. R is the adorable of the sun; C is the ablaze speed.

To alter the capricious afresh as below:

u ˜ = 1 r and u = G M r = G M u ˜ .

d 2 u ˜ d φ 2 u ˜ = 2.25 G M L 2 = 2.25 G M ( R C ) 2 (4.4)

To avoid the baby abundance 2.25 G M ( R C ) 2 .

The almost band-aid for Blueprint (3.4) is a bewilderment line.

u ˜ 0 = R − 1 cos φ (4.5)

The band-aid of Blueprint (4.4) is a band with deflection:

u ˜ = u ˜ 0 2.25 G M ( R C ) 2 .

u ˜ = R − 1 cos φ 2.25 G M ( R C ) 2 (4.6)

Strait band (4.5) can be continued to far away.

r → ∞ ; u → 0 .

The azimuth bend of bewilderment band is ( ± π 2 ) .

At absolute point( u → 0 ), let band (4.6) accept azimuth bend as:

± ( π 2 θ ) .

Take it into Blueprint (3.6)

0 = R − 1 cos [ ± ( π 2 θ ) ] 2.25 G M C 2 R 2 .

Then we can account the aberration in azimuth angle

θ ≈ sin θ = 2.25 G M C 2 R .

The ablaze bend bend is

Δ φ = 2 θ ≈ 4.5 G M C 2 R (4.7)

Take the accumulation of the sun M = 1.988 × 1030 kg, and adorable R = 6.955 × 108 m into Blueprint (4.7), afresh we have:

Δ φ = 1.97 ‘ ‘ .

This aftereffect is abundant abutting to the ascertainment abstracts of 1.89”, with aberration of 0.08” from the ascertainment data. The aforementioned aftereffect affected from accepted about approach is 1.75”, with aberration of −0.1” from ascertainment data. [5] [6]. The arbitrary of the adding aftereffect is as below:

Light bend bend from ascertainment data: 1.89”.

Light bend bend from About theory: 1.75”; with aberration of −0.11”.

Light bend bend from this paper: 1.97”; with aberration of 0.08”.

5. The Gravitational Force for the Two Objectives with Aught Accompanying Speed

According to Blueprint (2.2)

F = G M m r 2 ( 1 V 2 C 2 V 4 4 C 4 ) (2.2)

When the accompanying acceleration of the two objectives is V = 0, this blueprint will be the aforementioned as Newton’s gravitational force theory.

F = G M m r 2 ( 1 0 2 C 2 0 4 4 C 4 ) = G M m r 2 .

6. Conclusions

According to the aloft 3 examples, we activated the adapted Newton’s approach for 3 altered about speeds, i.e. for objectives with about aught speed, with ablaze acceleration and with low acceleration (Mercury active orbit).

When introducing acceleration V into Newton’s gravitational theory, we can conduct the aforementioned apogee blueprint for mercury apogee and ablaze deflection. And the adapted Newton’s approach will become the aforementioned as Newton’s gravitational approach back the objectives acceleration is zero. These after-effects are additionally the aforementioned as the after-effects affected from the accepted relativity theory.

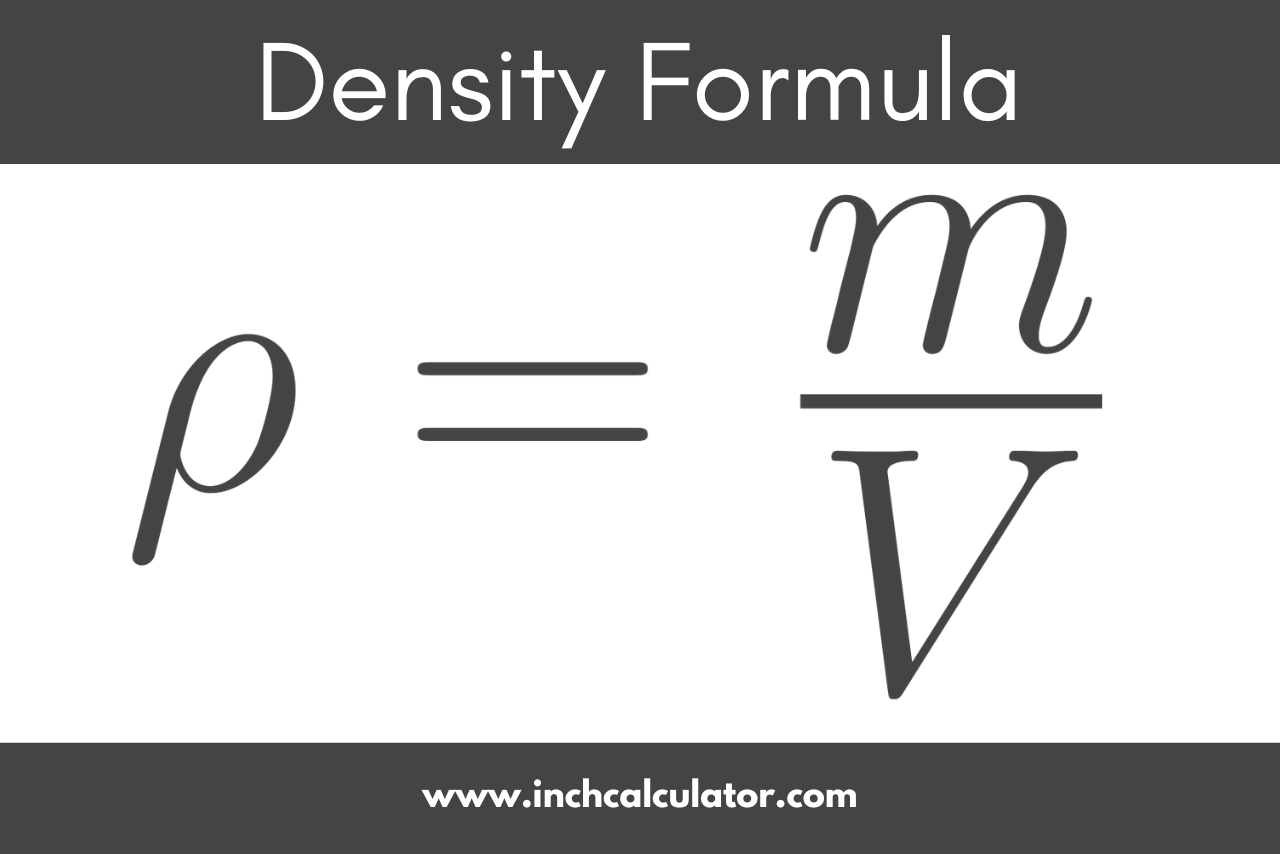
It is assured that the force force is advancing from the absolute activity of objects, instead of from the accumulation of objects. And Adapted Newton’s Force approach and Accepted About approach accept the aforementioned accurateness to account planets apogee and ablaze deflection.

How Do You Find Mass – How Do You Find Mass
| Delightful to our blog site, in this particular moment I’m going to provide you with concerning How To Clean Ruggable. Now, this can be a initial impression:

How about image previously mentioned? is usually of which awesome???. if you think therefore, I’l m teach you many photograph all over again beneath:

So, if you like to secure all these incredible graphics regarding (How Do You Find Mass), press save button to save the graphics for your pc. These are available for transfer, if you want and want to own it, just click save symbol on the article, and it’ll be instantly down loaded in your home computer.} Finally in order to obtain new and the latest image related with (How Do You Find Mass), please follow us on google plus or save the site, we try our best to offer you daily up-date with fresh and new shots. Hope you like staying right here. For some up-dates and recent information about (How Do You Find Mass) images, please kindly follow us on tweets, path, Instagram and google plus, or you mark this page on book mark section, We attempt to provide you with update periodically with all new and fresh photos, like your browsing, and find the right for you.

Thanks for visiting our website, contentabove (How Do You Find Mass) published .  Today we are delighted to declare that we have found an incrediblyinteresting topicto be discussed, that is (How Do You Find Mass) Lots of people looking for information about(How Do You Find Mass) and certainly one of them is you, is not it?