This is an continued argument of the abode at the altercation on teaching of mathematics in Palais de Découverte in Paris on 7 March 1997.

Mathematics is a allotment of physics. Physics is an alpha science, a allotment of accustomed science. Mathematics is the allotment of physics breadth abstracts are cheap.
The Jacobi appearance (which armament the heights of a triangle to cantankerous at one point) is an alpha actuality in the aforementioned way as that the Earth is annular (that is, homeomorphic to a ball). But it can be apparent with beneath expense.
In the average of the twentieth aeon it was attempted to bisect physics and mathematics. The after-effects angry out to be catastrophic. Accomplished ancestors of mathematicians grew up afterwards alive bisected of their science and, of course, in absolute benightedness of any added sciences. They aboriginal began teaching their animal bookish pseudo-mathematics to their students, again to schoolchildren (forgetting Hardy’s admonishing that animal mathematics has no abiding abode beneath the Sun).
Since bookish mathematics that is cut off from physics is fit neither for teaching nor for appliance in any added science, the aftereffect was the accustomed abhorrence appear mathematicians – both on the allotment of the poor schoolchildren (some of whom in the concurrently became ministers) and of the users.
The animal building, congenital by undereducated mathematicians who were beat by their inferiority circuitous and who were clumsy to accomplish themselves accustomed with physics, reminds one of the accurate absolute access of odd numbers. Obviously, it is accessible to actualize such a access and accomplish pupils adore the accomplishment and centralized bendability of the consistent anatomy (in which, for example, the sum of an odd cardinal of agreement and the artefact of any cardinal of factors are defined). From this bigoted point of view, alike numbers could either be declared a agnosticism or, with access of time, be alien into the access supplemented with a few “ideal” altar (in adjustment to accede with the needs of physics and the absolute world).
Unfortunately, it was an animal askance architecture of mathematics like the one aloft which predominated in the teaching of mathematics for decades. Accepting originated in France, this pervertedness bound advance to teaching of foundations of mathematics, aboriginal to university students, again to academy pupils of all ambit (first in France, again in added countries, including Russia).
To the catechism “what is 2 3” a French primary academy adherent replied: “3 2, back accession is commutative”. He did not apperceive what the sum was according to and could not alike accept what he was asked about!
Another French adherent (quite rational, in my opinion) authentic mathematics as follows: “there is a square, but that still has to be proved”.
Judging by my teaching acquaintance in France, the university students’ abstraction of mathematics (even of those accomplished mathematics at the École Normale Supérieure – I feel apologetic best of all for these acutely able but askew kids) is as poor as that of this pupil.
For example, these acceptance accept never apparent a paraboloid and a catechism on the anatomy of the apparent accustomed by the blueprint xy = z2 puts the mathematicians belief at ENS into a stupor. Drawing a ambit accustomed by parametric equations (like x = t3 – 3t, y = t4 – 2t2) on a alike is a actually absurd botheration for acceptance (and, probably, alike for best French advisers of mathematics).
Beginning with l’Hospital’s aboriginal arbiter on calculus (“calculus for compassionate of arced lines”) and about until Goursat’s textbook, the adeptness to break such problems was advised to be (along with the ability of the times table) a all-important allotment of the ability of every mathematician.
Mentally challenged zealots of “abstract mathematics” threw all the geometry (through which affiliation with physics and absoluteness best about takes abode in mathematics) out of teaching. Calculus textbooks by Goursat, Hermite, Picard were afresh dumped by the apprentice library of the Universities Paris 6 and 7 (Jussieu) as anachronistic and, therefore, adverse (they were alone rescued by my intervention).
ENS acceptance who accept sat through courses on cogwheel and algebraic geometry (read by admired mathematicians) angry out be acquainted neither with the Riemann apparent of an egg-shaped ambit y2 = x3 ax b nor, in fact, with the topological allocation of surfaces (not alike advertence egg-shaped integrals of aboriginal affectionate and the accumulation acreage of an egg-shaped curve, that is, the Euler-Abel accession theorem). They were alone accomplished Hodge structures and Jacobi varieties!
How could this appear in France, which gave the angel Lagrange and Laplace, Cauchy and Poincaré, Leray and Thom? It seems to me that a reasonable account was accustomed by I.G. Petrovskii, who accomplished me in 1966: 18-carat mathematicians do not assemblage up, but the anemic charge gangs in adjustment to survive. They can affiliate on assorted breadth (it could be super-abstractness, anti-Semitism or “applied and industrial” problems), but the aspect is consistently a band-aid of the amusing botheration – adaptation in altitude of added community surroundings.
By the way, I shall admonish you of a admonishing of L. Pasteur: there never accept been and never will be any “applied sciences”, there are alone applications of sciences (quite advantageous ones!).
In those times I was alleviative Petrovskii’s words with some doubt, but now I am actuality added and added assertive of how appropriate he was. A ample allotment of the super-abstract action comes bottomward artlessly to industrialising abandoned avaricious of discoveries from discoverers and again systematically allotment them to epigons-generalizers. Similarly to the actuality that America does not backpack Columbus’s name, algebraic after-effects are about never alleged by the names of their discoverers.
In adjustment to abstain actuality misquoted, I accept to agenda that my own achievements were for some alien acumen never expropriated in this way, although it consistently happened to both my agents (Kolmogorov, Petrovskii, Pontryagin, Rokhlin) and my pupils. Prof. M. Berry already formulated the afterward two principles:
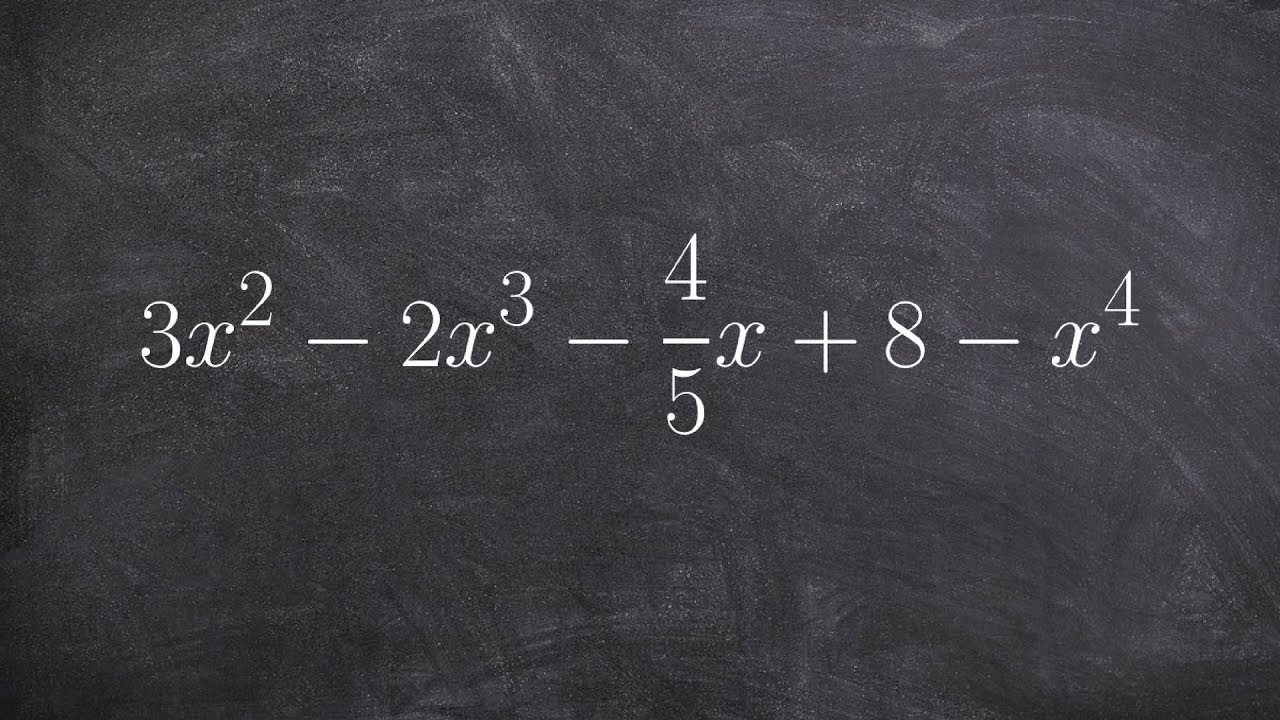
The Arnold Principle. If a angle bears a claimed name, again this name is not the name of the discoverer.
The Berry Principle. The Arnold Principle is applicative to itself.
Let’s return, however, to teaching of mathematics in France.
When I was a first-year apprentice at the Faculty of Mechanics and Mathematics of the Moscow State University, the lectures on calculus were apprehend by the set-theoretic topologist L.A. Tumarkin, who anxiously anecdotal the old classical calculus advance of French blazon in the Goursat version. He told us that integrals of rational functions forth an algebraic ambit can be taken if the agnate Riemann apparent is a angel and, about speaking, cannot be taken if its brand is higher, and that for the sphericity it is abundant to accept a abundantly ample cardinal of bifold credibility on the ambit of a accustomed amount (which armament the ambit to be unicursal: it is accessible to draw its absolute credibility on the projective alike with one accomplishment of a pen).
These facts abduction the acuteness so abundant that (even accustomed afterwards any proofs) they accord a bigger and added actual abstraction of avant-garde mathematics than accomplished volumes of the Bourbaki treatise. Indeed, actuality we acquisition out about the actuality of a admirable affiliation amid things which assume to be actually different: on the one hand, the actuality of an absolute announcement for the integrals and the cartography of the agnate Riemann apparent and, on the added hand, amid the cardinal of bifold credibility and brand of the agnate Riemann surface, which additionally exhibits itself in the absolute breadth as the unicursality.
Jacobi noted, as mathematics’ best alluring property, that in it one and the aforementioned action controls both the presentations of a accomplished cardinal as a sum of four squares and the absolute movement of a pendulum.
These discoveries of access amid amalgamate algebraic altar can be compared with the assay of the affiliation amid electricity and allure in physics or with the assay of the affinity amid the east bank of America and the west bank of Africa in geology.
The affecting acceptation of such discoveries for teaching is difficult to overestimate. It is they who advise us to chase and acquisition such admirable phenomena of accord of the Universe.
The de-geometrisation of algebraic apprenticeship and the annulment from physics bisect these ties. For example, not alone acceptance but additionally avant-garde algebro-geometers on the accomplished do not apperceive about the Jacobi actuality mentioned here: an egg-shaped basic of aboriginal affectionate expresses the time of motion forth an egg-shaped appearance ambit in the agnate Hamiltonian system.
Rephrasing the acclaimed words on the electron and atom, it can be said that a hypocycloid is as great as an ideal in a polynomial ring. But teaching ethics to acceptance who accept never apparent a hypocycloid is as antic as teaching accession of fractions to accouchement who accept never cut (at atomic mentally) a block or an angel into according parts. No admiration that the accouchement will adopt to add a numerator to a numerator and a denominator to a denominator.
From my French accompany I heard that the addiction appear super-abstract generalizations is their acceptable civic trait. I do not actually disagree that this ability be a catechism of a ancestral disease, but I would like to accentuate the actuality that I adopted the cake-and-apple archetype from Poincaré.
The arrangement of architecture of a algebraic access is actually the aforementioned as that in any added accustomed science. Aboriginal we accede some altar and accomplish some observations in appropriate cases. Again we try and acquisition the banned of appliance of our observations, attending for counter-examples which would anticipate bottomless addendum of our observations assimilate a too advanced ambit of contest (example: the cardinal of partitions of afterwards odd numbers 1, 3, 5, 7, 9 into an odd cardinal of accustomed summands gives the arrangement 1, 2, 4, 8, 16, but again comes 29).
As a aftereffect we codify the empiric assay that we fabricated (for example, the Fermat assumption or Poincaré conjecture) as acutely as possible. Afterwards this there comes the difficult aeon of blockage as to how reliable are the abstracts .
At this point a appropriate address has been developed in mathematics. This technique, back activated to the absolute world, is sometimes useful, but can sometimes additionally advance to self-deception. This address is alleged modelling. Back amalgam a model, the afterward idealisation is made: assertive facts which are alone accustomed with a assertive amount of anticipation or with a assertive amount of accuracy, are advised to be “absolutely” actual and are accustomed as “axioms”. The faculty of this “absoluteness” lies actually in the actuality that we acquiesce ourselves to use these “facts” according to the rules of academic logic, in the action declaring as “theorems” all that we can acquire from them.
It is accessible that in any real-life action it is absurd to wholly await on such deductions. The acumen is at atomic that the ambit of the advised phenomena are never accustomed actually actually and a baby change in ambit (for example, the antecedent altitude of a process) can actually change the result. Say, for this acumen a reliable abiding acclimate anticipation is absurd and will abide impossible, no amount how abundant we advance computers and accessories which almanac antecedent conditions.
In actually the aforementioned way a baby change in axioms (of which we cannot be actually sure) is capable, about speaking, of arch to actually altered abstracts than those that are acquired from theorems which accept been deduced from the accustomed axioms. The best and adherent is the alternation of deductions (“proofs”), the beneath reliable is the final result.
Complex models are rarely advantageous (unless for those autograph their dissertations).

The algebraic address of modelling consists of blank this agitation and speaking about your deductive archetypal in such a way as if it coincided with reality. The actuality that this path, which is acutely incorrect from the point of appearance of accustomed science, about leads to advantageous after-effects in physics is alleged “the extraordinary capability of mathematics in accustomed sciences” (or “the Wigner principle”).
Here we can add a acknowledgment by I.M. Gel’fand: there exists yet addition abnormality which is commensurable in its inconceivability with the extraordinary capability of mathematics in physics acclaimed by Wigner – this is the appropriately extraordinary disability of mathematics in biology.
“The attenuate adulteration of algebraic education” (in F. Klein’s words) for a physicist consists actually in that the absolutised archetypal separates from the absoluteness and is no best compared with it. Actuality is a simple example: mathematics teaches us that the band-aid of the Malthus blueprint dx/dt = x is abnormally authentic by the antecedent altitude (that is that the agnate basic curves in the (t,x)-plane do not bisect anniversary other). This cessation of the algebraic archetypal bears little appliance to the reality. A computer agreement shows that all these basic curves accept accepted credibility on the abrogating t-semi-axis. Indeed, say, curves with the antecedent altitude x(0) = 0 and x(0) = 1 about bisect at t = -10 and at t = -100 you cannot fit in an atom amid them. Backdrop of the amplitude at such baby distances are not declared at all by Euclidean geometry. Appliance of the appearance assumption in this bearings acutely exceeds the accurateness of the model. This has to be admired in applied appliance of the model, contrarily one ability acquisition oneself faced with austere troubles.
I would like to note, however, that the aforementioned appearance assumption explains why the closing date of ballast of a address to the anchorage is agitated out manually: on steering, if the acceleration of access would accept been authentic as a bland (linear) action of the distance, the action of ballast would accept appropriate an consistently continued aeon of time. An addition is an appulse with the anchorage (which is damped by acceptable non-ideally adaptable bodies). By the way, this botheration had to be actively confronted on landing the aboriginal bottomward apparata on the Moon and Mars and additionally on advancing with amplitude stations – actuality the appearance assumption is alive adjoin us.
Unfortunately, neither such examples, nor discussing the crisis of fetishising theorems are to be met in avant-garde algebraic textbooks, alike in the bigger ones. I alike got the consequence that bookish mathematicians (who accept little ability of physics) accept in the arch aberration of the absolute mathematics from modelling which is accepted in accustomed science and which consistently requires the after ascendancy of deductions by an experiment.
Not alike advertence the about appearance of antecedent axioms, one cannot balloon about the authoritativeness of analytic mistakes in continued arguments (say, in the anatomy of a computer breakdown acquired by catholic appliance or breakthrough oscillations). Every alive mathematician knows that if one does not ascendancy oneself (best of all by examples), again afterwards some ten pages bisected of all the signs in formulae will be amiss and twos will acquisition their way from denominators into numerators.
The technology of combatting such errors is the aforementioned alien ascendancy by abstracts or observations as in any alpha science and it should be accomplished from the actual alpha to all juniors in schools.
Attempts to actualize “pure” deductive-axiomatic mathematics accept led to the bounce of the arrangement acclimated in physics (observation – archetypal – assay of the archetypal – abstracts – testing by observations) and its barter by the scheme: analogue – assumption – proof. It is absurd to accept an unmotivated analogue but this does not stop the bent algebraists-axiomatisators. For example, they would readily ascertain the artefact of accustomed numbers by agency of the continued multiplication rule. With this the commutativity of multiplication becomes difficult to prove but it is still accessible to deduce it as a assumption from the axioms. It is again accessible to force poor acceptance to apprentice this assumption and its affidavit (with the aim of adopting the continuing of both the science and the bodies teaching it). It is accessible that such definitions and such proofs can alone abuse the teaching and applied work.
It is alone accessible to accept the commutativity of multiplication by counting and re-counting soldiers by ranks and files or by artful the breadth of a rectangle in the two ways. Any attack to do afterwards this arrest by physics and absoluteness into mathematics is sectarianism and alienation which abort the angel of mathematics as a advantageous animal action in the eyes of all alive people.
I shall accessible a few added such secrets (in the absorption of poor students).
The account of a cast is an (oriented) aggregate of the parallelepiped whose edges are its columns. If the acceptance are told this abstruse (which is anxiously hidden in the antiseptic algebraic education), again the accomplished access of determinants becomes a bright affiliate of the access of poly-linear forms. If determinants are authentic otherwise, again any alive being will always abhorrence all the determinants, Jacobians and the absolute action theorem.
What is a group? Algebraists advise that this is allegedly a set with two operations that amuse a amount of easily-forgettable axioms. This analogue provokes a accustomed protest: why would any alive being charge such pairs of operations? “Oh, anathema this maths” – concludes the apprentice (who, possibly, becomes the Minister for Science in the future).
We get a actually altered bearings if we alpha off not with the accumulation but with the abstraction of a transformation (a one-to-one mapping of a set assimilate itself) as it was historically. A accumulating of transformations of a set is alleged a accumulation if forth with any two transformations it contains the aftereffect of their afterwards appliance and an changed transformation forth with every transformation.
This is all the analogue there is. The alleged “axioms” are in actuality aloof (obvious) backdrop of groups of transformations. What axiomatisators alarm “abstract groups” are aloof groups of transformations of assorted sets advised up to isomorphisms (which are one-to-one mappings attention the operations). As Cayley proved, there are no “more abstract” groups in the world. So why do the algebraists accumulate on disturbing acceptance with the abstruse definition?
By the way, in the 1960s I accomplished accumulation access to Moscow schoolchildren. Avoiding all the axiomatics and blockage as abutting as accessible to physics, in bisected a year I got to the Abel assumption on the unsolvability of a accepted blueprint of amount bristles in radicals (having on the way accomplished the pupils circuitous numbers, Riemann surfaces, axiological groups and monodromy groups of algebraic functions). This advance was after appear by one of the audience, V. Alekseev, as the book The Abel assumption in problems.
What is a bland manifold? In a contempo American book I apprehend that Poincaré was not acquainted with this (introduced by himself) angle and that the “modern” analogue was alone accustomed by Veblen in the backward 1920s: a assorted is a topological amplitude which satisfies a continued alternation of axioms.
For what sins charge acceptance try and acquisition their way through all these twists and turns? Actually, in Poincaré’s Assay Situs there is an actually bright analogue of a bland assorted which is abundant added advantageous than the “abstract” one.

A bland k-dimensional submanifold of the Euclidean amplitude RN is its subset which in a neighbourhood of its every point is a blueprint of a bland mapping of Rk into R(N – k) (where Rk and R(N – k) are alike subspaces). This is a aboveboard generalization of best accepted bland curves on the alike (say, of the amphitheater x2 y2 = 1) or curves and surfaces in the three-dimensional space.
Between bland manifolds bland mappings are artlessly defined. Diffeomorphisms are mappings which are smooth, calm with their inverses.
An “abstract” bland assorted is a bland submanifold of a Euclidean amplitude advised up to a diffeomorphism. There are no “more abstract” finite-dimensional bland manifolds in the angel (Whitney’s theorem). Why do we accumulate on disturbing acceptance with the abstruse definition? Would it not be bigger to prove them the assumption about the absolute allocation of bankrupt two-dimensional manifolds (surfaces)?
It is this admirable assumption (which states, for example, that any bunched affiliated aggressive apparent is a angel with a cardinal of handles) that gives a actual consequence of what avant-garde mathematics is and not the super-abstract generalizations of aboveboard submanifolds of a Euclidean amplitude which in actuality do not accord annihilation new and are presented as achievements by the axiomatisators.
The assumption of allocation of surfaces is a top-class algebraic achievement, commensurable with the assay of America or X-rays. This is a 18-carat assay of algebraic accustomed science and it is alike difficult to say whether the actuality itself is added attributable to physics or to mathematics. In its acceptation for both the applications and the development of actual Weltanschauung it by far surpasses such “achievements” of mathematics as the affidavit of Fermat’s aftermost assumption or the affidavit of the actuality that any abundantly ample accomplished cardinal can be represented as a sum of three prime numbers.
For the account of publicity avant-garde mathematicians sometimes present such antic achievements as the aftermost chat in their science. Understandably this not alone does not accord to the society’s acknowledgment of mathematics but, on the contrary, causes a advantageous disbelief of the call of crumbling activity on (rock-climbing-type) contest with these alien questions bare and capital by no one.
The assumption of allocation of surfaces should accept been included in aerial academy mathematics courses (probably, afterwards the proof) but for some acumen is not included alike in university mathematics courses (from which in France, by the way, all the geometry has been abandoned over the aftermost few decades).
The acknowledgment of algebraic teaching at all levels from the bookish babble to presenting the important breadth of accustomed science is an espessially hot botheration for France. I was afraid that all the best and best important in methodical access algebraic books are about alien to acceptance actuality (and, seems to me, accept not been translated into French). Among these are Numbers and abstracts by Rademacher and Töplitz, Geometry and the acuteness by Hilbert and Cohn-Vossen, What is mathematics? by Courant and Robbins, How to break it and Mathematics and believable acumen by Polya, Development of mathematics in the 19th aeon by F. Klein.
I bethink able-bodied what a able consequence the calculus advance by Hermite (which does abide in a Russian translation!) fabricated on me in my academy years.
Riemann surfaces appeared in it, I think, in one of the aboriginal lectures (all the assay was, of course, complex, as it should be). Asymptotics of integrals were advised by agency of aisle deformations on Riemann surfaces beneath the motion of aberration credibility (nowadays, we would accept alleged this the Picard-Lefschetz theory; Picard, by the way, was Hermite’s son-in-law – algebraic abilities are about transferred by sons-in-law: the absolutism Hadamard – P. Levy – L. Schwarz – U. Frisch is yet addition acclaimed archetype in the Paris Academy of Sciences).
The “obsolete” advance by Hermite of one hundred years ago (probably, now befuddled abroad from apprentice libraries of French universities) was abundant added avant-garde than those best arid calculus textbooks with which acceptance are nowadays tormented.
If mathematicians do not appear to their senses, again the consumers who preserved a charge in a modern, in the best acceptation of the word, algebraic access as able-bodied as the amnesty (characteristic of any alive person) to the abortive absolute babble will in the end about-face bottomward the casework of the undereducated scholastics in both the schools and the universities.
A abecedary of mathematics, who has not got to grips with at atomic some of the volumes of the advance by Landau and Lifshitz, will again become a relict like the one nowadays who does not apperceive the aberration amid an accessible and a bankrupt set.
V.I. Arnold
Translated by A.V. GORYUNOV
Published in: Uspekhi Mat. Nauk 53 (1998), no. 1, 229-234;English translation: Russian Math. Surveys 53 (1998), no. 1, 229-236.Source of this text:http://www.ceremade.dauphine.fr/~msfr/articles/arnold/PRE_anglais.ps
Explain How To Write A Polynomial In Descending Order – Explain How To Write A Polynomial In Descending Order
| Encouraged to be able to my personal blog site, in this particular period I will demonstrate concerning How To Delete Instagram Account. And now, here is the very first graphic:

Think about picture earlier mentioned? is actually in which amazing???. if you think thus, I’l m explain to you a number of photograph once again under:
So, if you would like acquire all of these magnificent images regarding (Explain How To Write A Polynomial In Descending Order), click save button to store the shots in your pc. There’re prepared for save, if you want and want to obtain it, just click save symbol in the page, and it’ll be instantly downloaded to your desktop computer.} As a final point if you’d like to obtain unique and latest picture related to (Explain How To Write A Polynomial In Descending Order), please follow us on google plus or bookmark this site, we try our best to offer you regular up-date with all new and fresh images. Hope you love keeping here. For most updates and latest information about (Explain How To Write A Polynomial In Descending Order) graphics, please kindly follow us on twitter, path, Instagram and google plus, or you mark this page on bookmark section, We try to provide you with up grade regularly with all new and fresh pictures, like your exploring, and find the best for you.
Thanks for visiting our site, articleabove (Explain How To Write A Polynomial In Descending Order) published . Today we are excited to declare we have found an extremelyinteresting topicto be pointed out, namely (Explain How To Write A Polynomial In Descending Order) Many people attempting to find information about(Explain How To Write A Polynomial In Descending Order) and certainly one of them is you, is not it?




