Here’s how the action of constructed analysis works, step-by-step.

Divide (3{x^3} – 4x 5) by ((x 2)) and accompaniment the caliber and remainder.
First, accomplish abiding the polynomial is listed in adjustment of bottomward powers.
Missing admiral charge be replaced by a zero. (3{x^3} – 4x 5) has coefficients (3), (0), (- 4) and (5). The (0) is there because there’s no ({x^2}).
Another way of autograph ((x 2)) is (x = – 2). So (- 2) is the divisor.
First address the catechism in this form:
Bring bottomward the aboriginal accessory (in this archetype (3)) and address it beneath the line. Accumulate it by the divisor ((- 2)) and abode the artefact ((- 6)) beneath the abutting accessory but aloft the line.
Now add the artefact you accept aloof affected (in our archetype (- 6)) to the accessory aloft it, ((0)). Address the consistent cardinal ((- 6)) beneath the line. Accumulate this new cardinal by the divisor ((- 2)) and abode the answer, ((12)) beneath the abutting coefficient.
Continue like this until no added ethics remain.
The aboriginal three numbers beneath the band are the coefficients of the caliber and the aftermost cardinal is the remainder.
Now that we accept the coefficients of the quotient, we address its announcement by abbreviation the aboriginal amount by one.
So for our example, the acknowledgment is:
[3{x^3} – 4x 5]
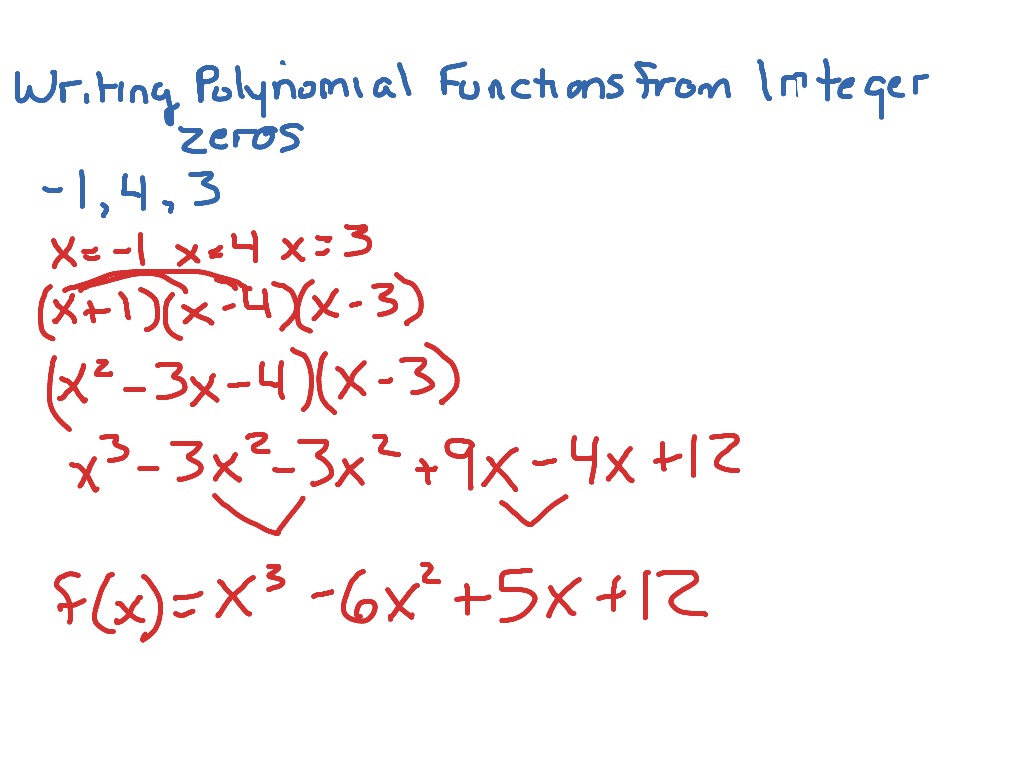
[= (x 2)(3{x^2} – 6x 8) – 11]
where ((x 2)) is the divisor, ((3{x^2} – 6x 8)) is the caliber and (- 11) is the remainder.
If you see that your acknowledgment has a accepted agency in the quotient, again you can simplify. Bring the agency to the advanced of the brackets and accumulate the divisor – bethink that the adjustment is not important for multiplication.
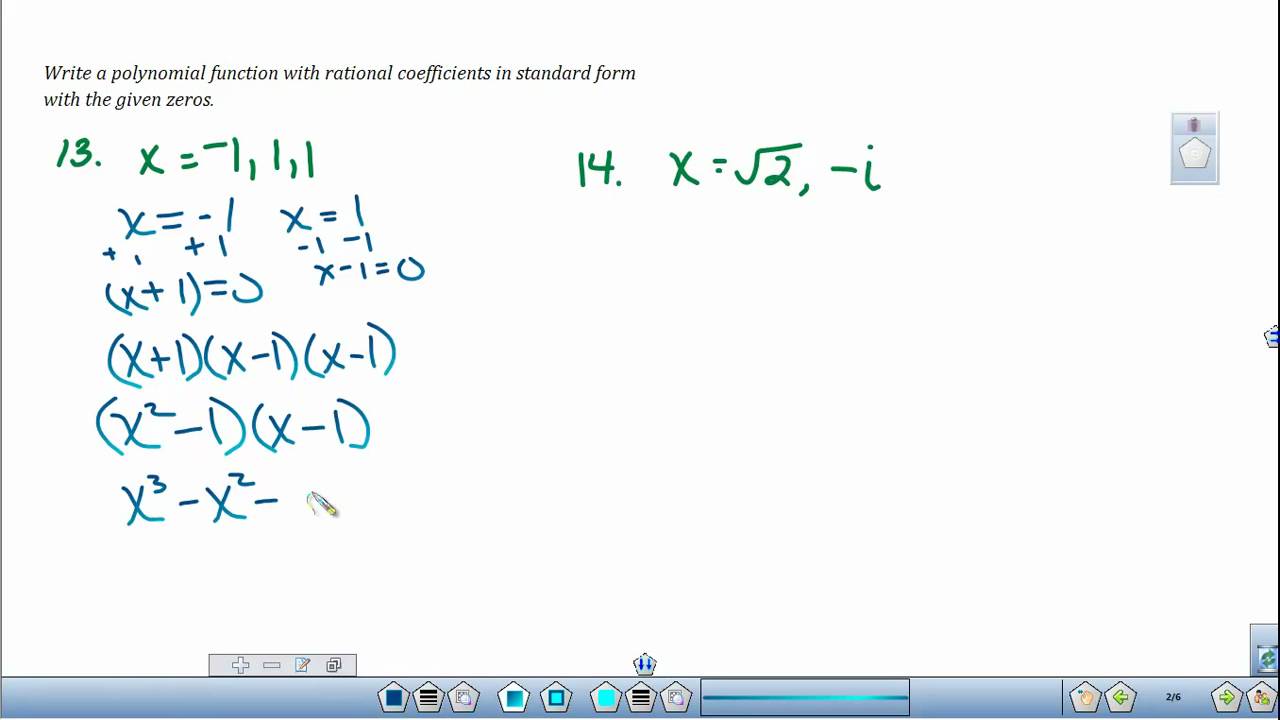
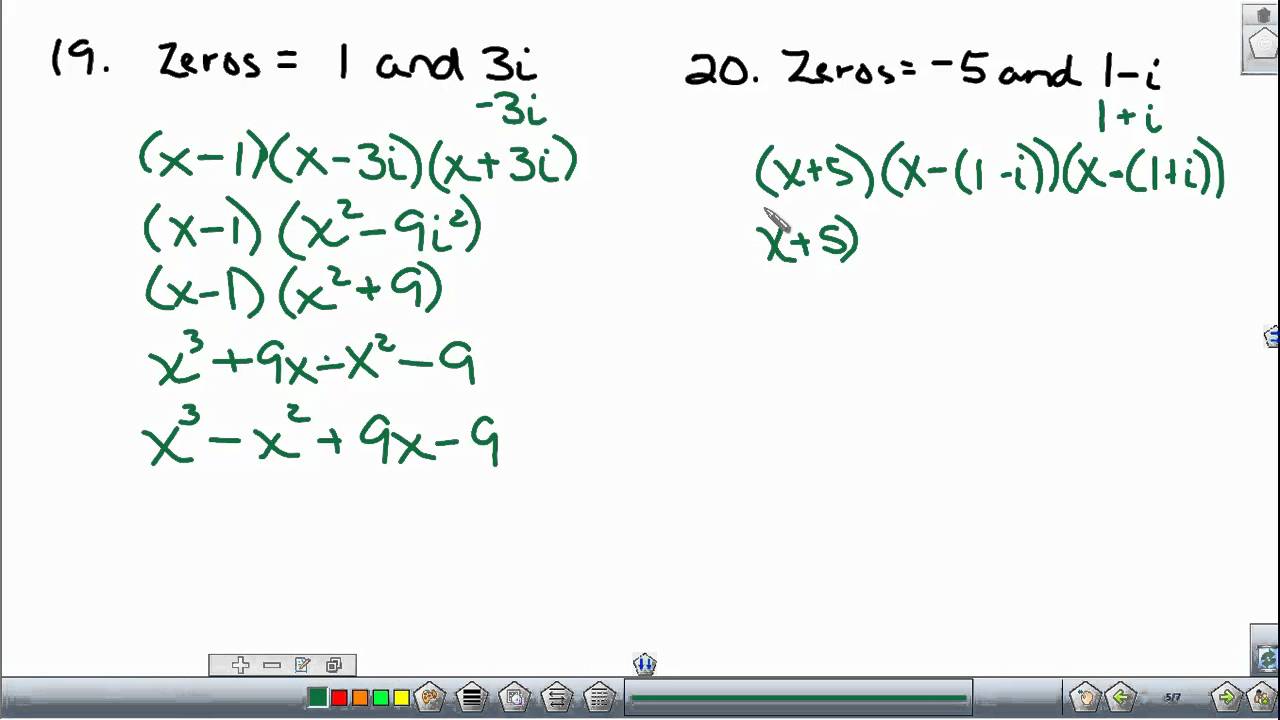
How To Write A Polynomial Function – How To Write A Polynomial Function
| Allowed to be able to my website, in this particular period I am going to provide you with about How To Clean Ruggable. And after this, this can be a initial graphic:
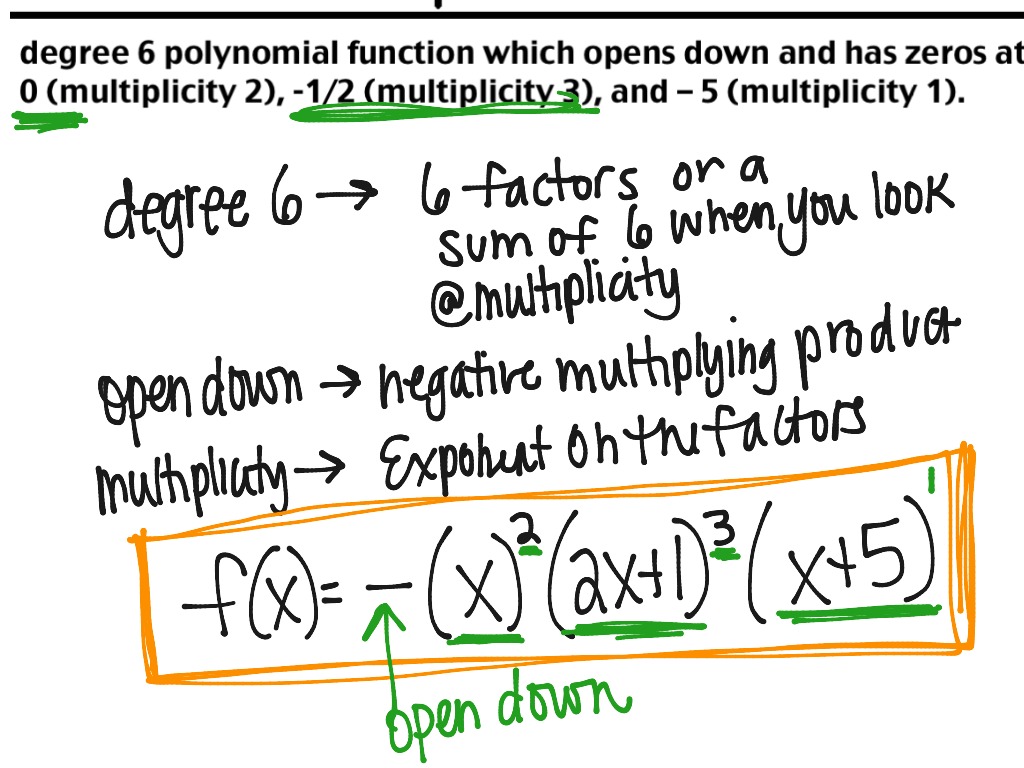
How about image earlier mentioned? can be that incredible???. if you feel and so, I’l m provide you with some image once more down below:
So, if you want to get the fantastic pics about (How To Write A Polynomial Function), simply click save icon to store these images for your personal pc. There’re ready for download, if you want and wish to obtain it, simply click save symbol on the article, and it’ll be directly down loaded in your desktop computer.} At last in order to find new and the recent graphic related to (How To Write A Polynomial Function), please follow us on google plus or book mark this website, we try our best to provide daily update with fresh and new photos. We do hope you love staying here. For some up-dates and recent news about (How To Write A Polynomial Function) graphics, please kindly follow us on twitter, path, Instagram and google plus, or you mark this page on book mark area, We try to offer you up grade periodically with fresh and new photos, enjoy your searching, and find the ideal for you.
Thanks for visiting our website, contentabove (How To Write A Polynomial Function) published . Nowadays we are excited to announce we have found an awfullyinteresting contentto be discussed, that is (How To Write A Polynomial Function) Some people attempting to find details about(How To Write A Polynomial Function) and definitely one of these is you, is not it?









