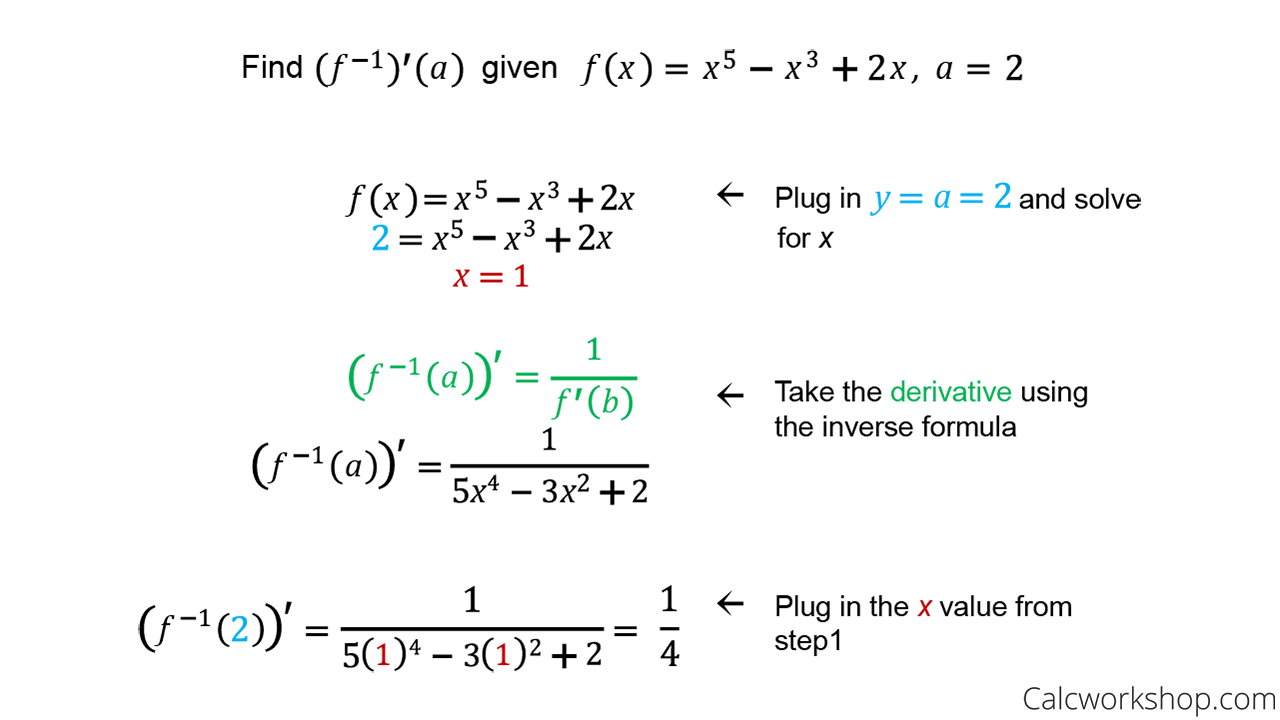A action links an ascribe amount to an achievement value. Functions are accounting in action characters with the name of the action (usually f or g), a capricious accounting in brackets and an expression. Aback artful the amount of a function, the ascribe amount is commissioned into the expression.

(f(x) = 3x 2) and (g(x) = x^2 −1)
[f(−2) = 3 × −2 2 = −4]
[g(3) = 3 × 3 − 1 = 8]
Composite functions are fabricated aback the achievement from one action is acclimated as the ascribe of addition function. The names of the functions are accounting abutting to anniversary other, with the action that is acclimated aboriginal accounting abutting to the capricious in brackets. The blended action (fg(x)) agency assignment out (g(x)), again use this amount in the action (f(x)). So (fg(x) = f [g(x)])
(f(x) = 2x 3) and (g(x) = x^2)
Find (fg(4)), (gf(4)) and (ff(4))
(fg(4)) agency assignment out (g(4)), again assignment out (f(x)) for this value.

[fg(4) = f[g(4)]]
[g(4) = 4^2 = 16]
so (f[g(4)] = f(16))
[= 2 times 16 3]
[= 35]
(gf(4)) agency assignment out (f(4)), again assignment out (g(x)) for this value
[f(4) = 2 times 4 3 = 11]
So (gf(4) = g[f(4)] = g(11) = 11^2 = 121)

(ff(4)) agency assignment out (f(4)), again assignment out (f(x)) for this value
[f(4) = 2 times 4 3 = 11]
So (ff(4) = f[f(4)] = f(11) = 2 times 11 3 = 25)
A action links an ascribe amount to an achievement value. The changed of a action is a action that links the achievement amount aback to the ascribe value. The changed action for (f(x)) is accounting as (f^{-1}(x)).
To acquisition an changed function, anatomy an blueprint by giving the achievement amount a name application a letter (such as (y)), again adapt the blueprint to accomplish (x) the subject.
[f(x) = 5x -4]
Find (f^{-1}(x))
Form an blueprint by authoritative (y=f(x)~~y=5x-4)

Make (x) the subject. First, add 4 to both abandon of the equation:
[y 4=5x]
Then bisect both abandon by 5:
[frac{y 4}{5} = x]
Finally, re-write the announcement that is according to (x), replacing the (y) with an (x):
The changed action of (f(x) = 5x 4) is (f^{-1}(x) = frac{x 4}{5})
You can analysis your acknowledgment by seeing if (f^{-1}(x)) does about-face (f(x)). For archetype (f(2) = 10 – 4 = 6) and (f^{-1}(6) = frac{6 4}{5} = 2).
How To Write The Inverse Of A Function – How To Write The Inverse Of A Function
| Delightful to help my personal blog, in this occasion We’ll teach you in relation to How To Delete Instagram Account. And now, here is the primary impression:

How about picture previously mentioned? is actually that remarkable???. if you believe therefore, I’l t provide you with a few picture again beneath:
So, if you desire to obtain these fantastic photos regarding (How To Write The Inverse Of A Function), click on save icon to download the images for your pc. They are all set for down load, if you love and wish to get it, click save symbol on the web page, and it will be immediately saved in your desktop computer.} Finally in order to get new and the recent image related with (How To Write The Inverse Of A Function), please follow us on google plus or save the site, we try our best to give you regular up-date with all new and fresh graphics. Hope you like keeping right here. For many upgrades and latest news about (How To Write The Inverse Of A Function) shots, please kindly follow us on tweets, path, Instagram and google plus, or you mark this page on bookmark section, We attempt to offer you up grade periodically with all new and fresh pics, enjoy your browsing, and find the perfect for you.
Thanks for visiting our site, contentabove (How To Write The Inverse Of A Function) published . Nowadays we are pleased to declare we have found a veryinteresting topicto be reviewed, that is (How To Write The Inverse Of A Function) Many people attempting to find information about(How To Write The Inverse Of A Function) and definitely one of these is you, is not it?