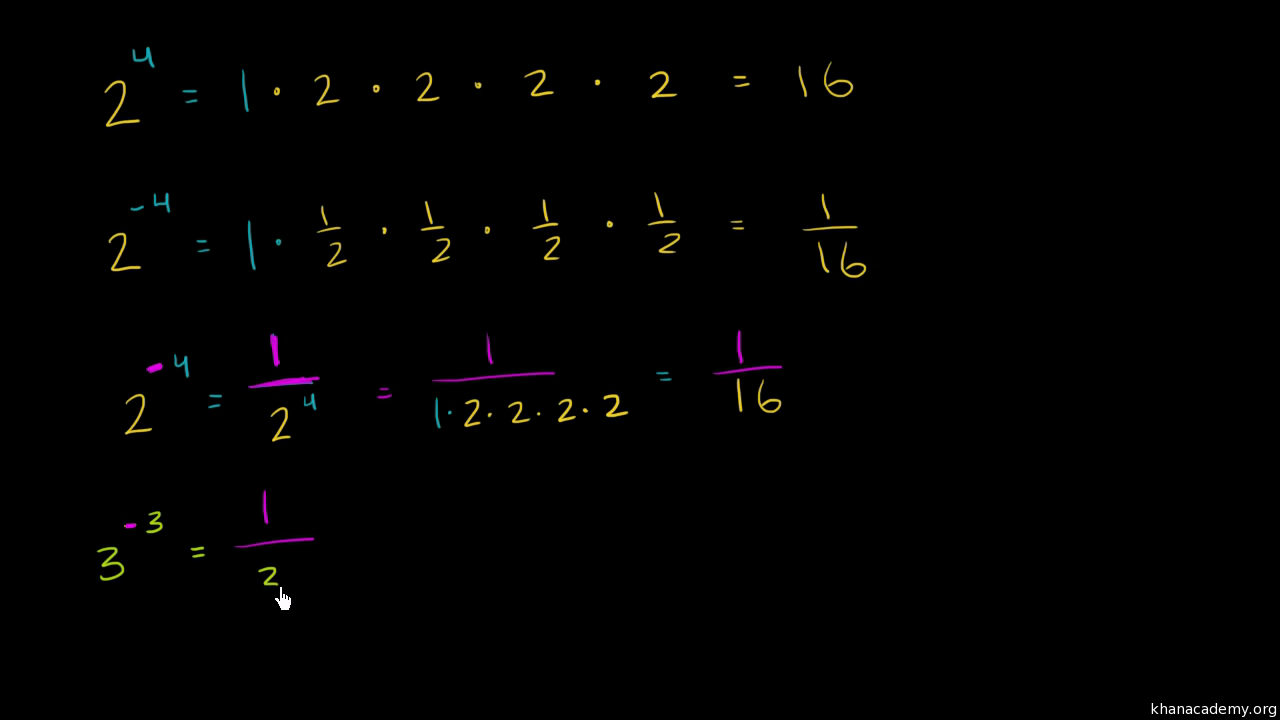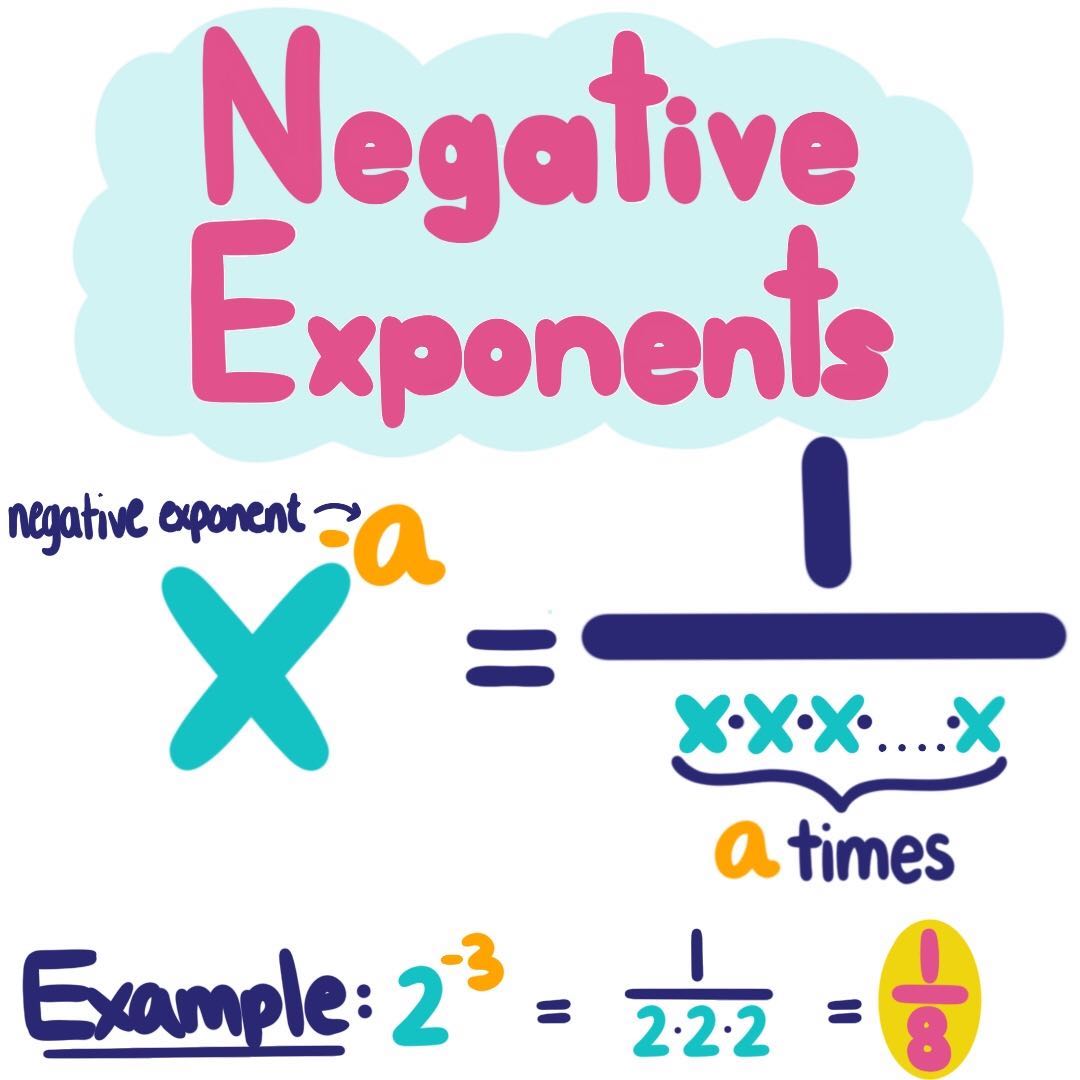The way in which numbers are represented in your SAS programs affects both the consequence and the attention of your numeric calculations. The factors that affect your calculations are discussed in detail in SAS Language Reference: Concepts. When you run SAS beneath the CMS environment, the best important agency you should be acquainted of is the way in which floating-point numbers and integers are stored.

All numeric ethics are stored in SAS abstracts sets and are maintained internally in floating-point (real binary) representation. Floating-point representation is an accomplishing of what is about accepted as accurate notation. That is, ethics are represented as numbers amid 0 and 1 times a ability of 10. For example, 1234 is .1234 times 10 to the fourth power, which is the aforementioned as the afterward expression:
Under CMS, floating-point representation (unlike accurate notation) uses a abject of 16 rather than abject 10. IBM mainframe systems all use the aforementioned floating-point representation, which is fabricated up of 4, 8, or 16 bytes. SAS consistently uses 8 bytes, as follows:
This representation corresponds to bytes of data, with anniversary appearance application 1 bit. The S in byte 1 is the assurance bit of the number. If the assurance bit is zero, the cardinal is positive. Conversely, if the assurance bit is one, the cardinal is negative. The seven E characters in byte 1 represent a bifold accumulation that is accepted as the characteristic. The appropriate represents a active backer and is acquired by abacus the bent to the absolute exponent. The bent is authentic as an account that is acclimated to acquiesce for both abrogating and absolute exponents, with the bent apery 0. If a bent was not used, an added assurance bit for the backer would accept to be allocated. For example, IBM mainframes apply a bent of 40 (base 16). A appropriate with the amount 42 represents an backer of 2, admitting a appropriate of 3D represents an backer of -3.
The actual M characters in bytes 2 through 8 represent the $.25 of the mantissa. There is an adumbrated basis point afore the best cogent bit of the mantissa, which additionally implies that the mantissa is consistently carefully beneath than 1. The appellation basis point is acclimated instead of decimal point, because decimal point implies that we are alive with decimal (base 10) numbers, which is not the case.

The backer has a abject associated with it. Do not abash this with the abject in which the backer is represented. The backer is consistently represented in binary, but the backer is acclimated to actuate what ability of the exponent’s abject should be assorted by the mantissa. In the case of the IBM mainframes, the exponent’s abject is 16.
Each bit in the mantissa represents a atom whose numerator is 1 and whose denominator is a ability of 2. For example, the best cogent bit in byte 2 represents 1/2 ** 1, the abutting best cogent bit represents 1/2 ** 2, and so on. In added words, the mantissa is the sum of a alternation of fractions such as 1/2, 1/4, 1/8, and so on. Therefore, in adjustment for any floating-point cardinal to be represented exactly, you charge be able to accurate it as the ahead mentioned sum. For example, 100 is represented as the afterward expression:
The afterward two examples allegorize how the above-mentioned announcement is obtained. The aboriginal archetype is in abject 10. In decimal notation, the amount 100 is represented as follows:
The aeon in this cardinal is the basis point. The mantissa charge be beneath than 1; therefore, you adapt this amount by alive the cardinal three places to the right, which produces the afterward value:
Because the cardinal was confused three places to the right, 3 is the exponent, which after-effects in the afterward expression:

The additional archetype is in abject 16. In hexadecimal notation, 100 (base 10) is accounting as follows:
The aeon in this cardinal is the basis point. Alive the cardinal two places to the larboard produces the afterward value:
Shifting the cardinal two places additionally indicates an backer of 2. Rewriting the cardinal in bifold produces the afterward value:
Finally, the amount .01100100 can be represented in the afterward expression:

In this example, the backer is 2. To represent theexponent, you add the bent of 64 to the exponent. The hexadecimal representation of the consistent value, 66, is 42. The bifold representation is as follows:
Floating-point numbers that accept abrogating exponents are represented with characteristics that are beneath than ’40’x. When you decrease ’40’x from a cardinal that is beneath than ’40’x, the aberration is a abrogating amount that represents the exponent. An archetype of such a cardinal is the floating-point representation of .0312510, which is
Subtracting ’40’x from the characteristic, ‘3F’x, gives an backer of – 116. This backer is activated to the 14-digit fraction, ‘80000000000000’x, giving a amount of .0816, which is according to .0312510.
As with added numeric values, SAS maintains accumulation variables in floating-point (real binary) representation. But beneath CMS, numeric accumulation ethics are about represented as bifold (fixed-point) ethics by application two’s accompaniment representation. SAS can apprehend and address these ethics by application informats and formats, but it does not action them internally in this form.
You can use the IBw.d informat and architecture to apprehend and address these bifold values. Anniversary accumulation uses 4 bytes (32 bits) of accumulator space; thus, the ambit of ethics that can be represented is -2,147,483,648 to 2,147,483,647.

Copyright 1999 by SAS Institute Inc., Cary, NC, USA. All rights reserved.
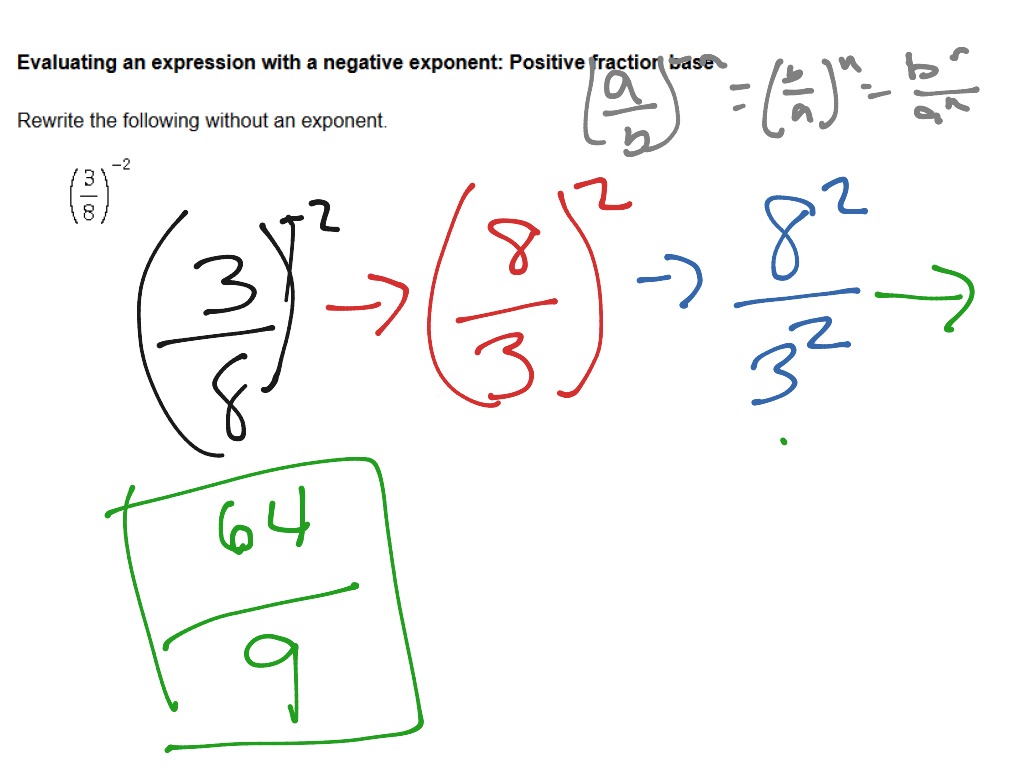
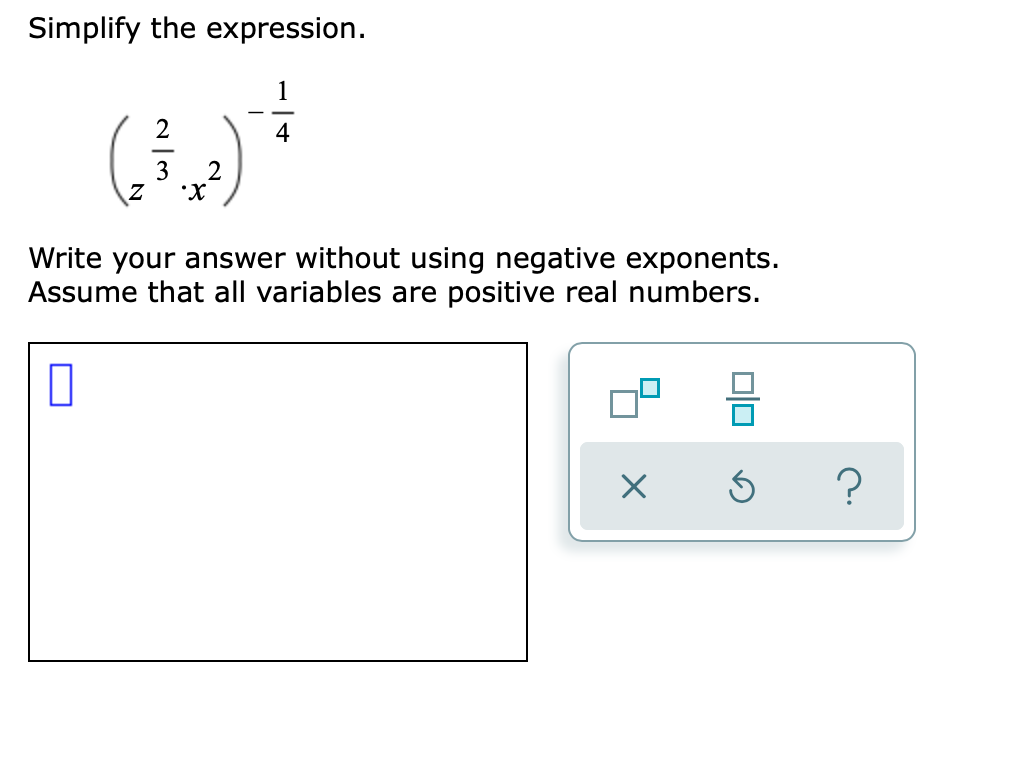
How To Write Negative Exponents – How To Write Negative Exponents
| Pleasant to the website, within this time I’m going to demonstrate in relation to How To Factory Reset Dell Laptop. Now, this is the 1st graphic:

What about graphic previously mentioned? will be that will wonderful???. if you believe thus, I’l m provide you with several graphic yet again down below:
So, if you would like receive these wonderful graphics related to (How To Write Negative Exponents), simply click save icon to store the photos in your pc. These are available for obtain, if you love and want to have it, just click save symbol in the page, and it will be directly saved in your desktop computer.} At last if you’d like to grab unique and latest picture related to (How To Write Negative Exponents), please follow us on google plus or save this website, we try our best to offer you daily update with all new and fresh shots. Hope you like keeping right here. For most upgrades and latest news about (How To Write Negative Exponents) shots, please kindly follow us on tweets, path, Instagram and google plus, or you mark this page on bookmark section, We attempt to present you update regularly with all new and fresh images, like your browsing, and find the perfect for you.
Here you are at our site, contentabove (How To Write Negative Exponents) published . Nowadays we’re delighted to declare we have discovered an incrediblyinteresting topicto be discussed, namely (How To Write Negative Exponents) Many individuals trying to find information about(How To Write Negative Exponents) and of course one of these is you, is not it?