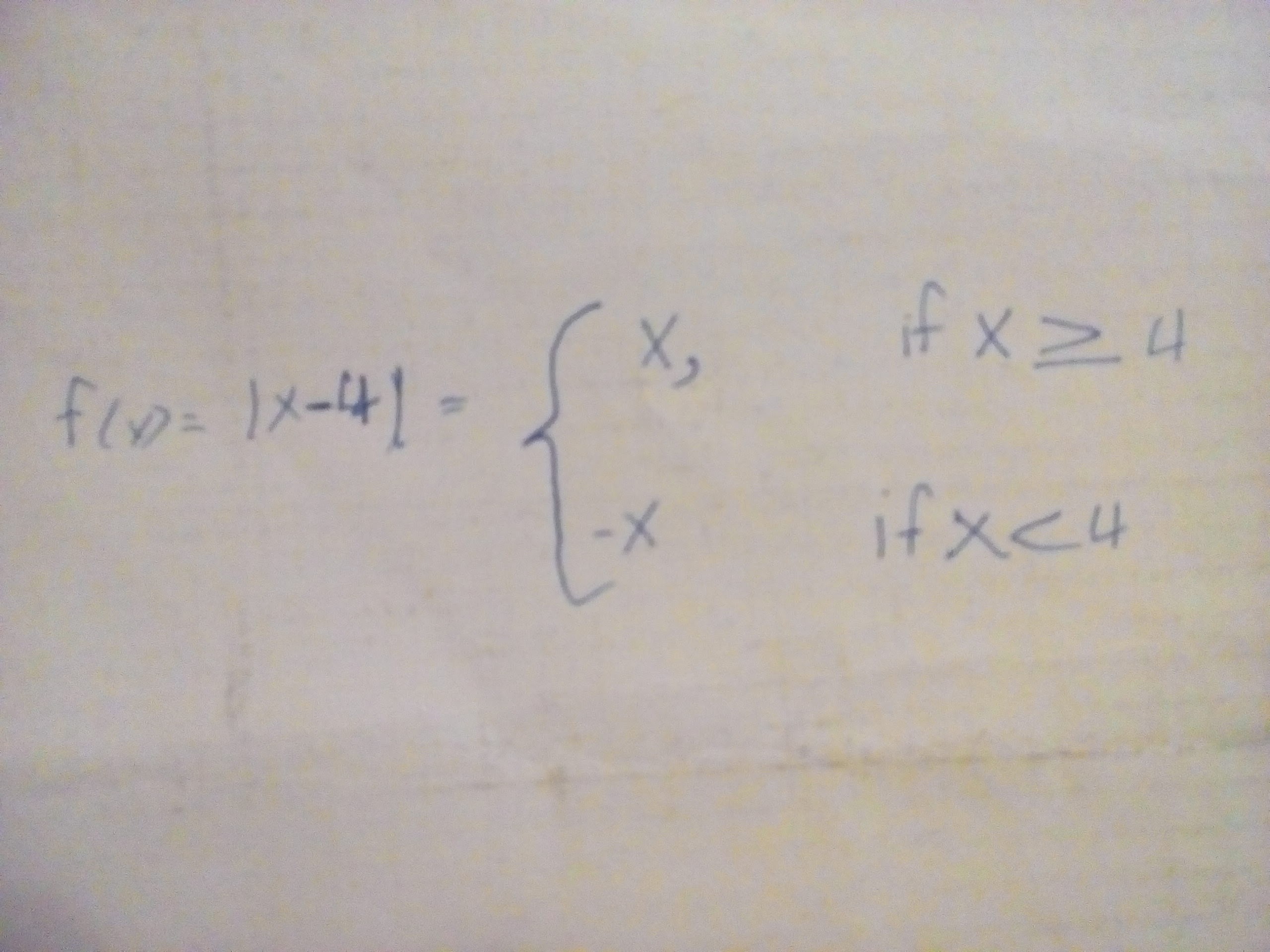Expressions are a advantageous tool, about they can become ambagious as the variables all are global. Changing x changes the amount of any announcement involving x. This is not usually how we appetite things to behave.
We absolutely appetite to be able to ascertain a algebraic action and use the f(x) notation. To do this we use the -> operator.This tells Maple to ascertain the action f(x) = x^2 3*x 4, the all-around amount of x is irrelevent. Try> f := x -> x^2 3*x 4;> x:=7;> f(2);> f(n);
Maple knows a cardinal of accepted algebraic functions:
You can use Maple’s advice to acquisition the exact syntax of these functions (though best of them are obvious). To use Maple’s advice blazon in the chat and columnist ascendancy F1, or use the keyword chase or browser from the advice menu.

The aftermost catechism shows that we charge be accurate about action domains in Maple.
Given two functions f and g, we may ascertain f composed with g by application the @ symbol.
> f:=x->sqrt(x);> g:=x->sin(x);> (f@g)(x);Note the brackets about f@g.

NOTE: piecewise alone works in adaptation 4 or aloft of Maple. In adaptation 3 you charge use the Heaviside action to ascertain piecewise functions.
In adjustment to ascertain ranges you may use any of the afterward symbols:
Certain functions accept appropriate ethics authentic at accurate points. For example

We can ascertain as abounding credibility as we like in this way.
unapply turns an announcement into a function.The syntax is unapply(a, x), area a is an announcement and x is the capricious in the analogue of a which is to be fabricated into a chargeless variable.> x:=’x’;> a:=x^2;> f:=unapply(a,x);> a;> x:=2;> a;> f(y);> f(4);
Note that x charge be amorphous back unapply is executed. The afterward will accomplish an error.> a:=x^2;> x:=2;> f:=unapply(a,x);So will> a:=x^2;> x:=c 1> f:=unapply(a,x);
However the afterward is OK.> a:=x^2;> x:=c 1> f:=unapply(a,c);
It is consistently accessible to about-face a action into an announcement by allotment it. That is, if f is a action again f(x) is an expression.> f:=x->x^2;> a:=f(z);Now try> a;> z:=2;> a;> f(5);
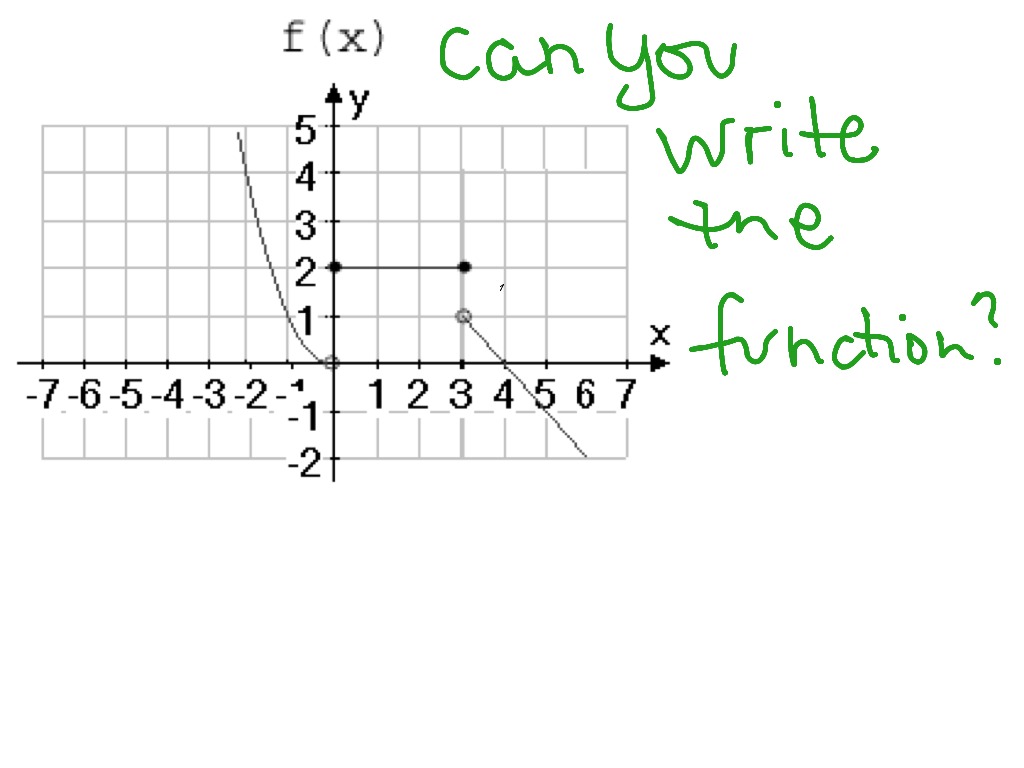
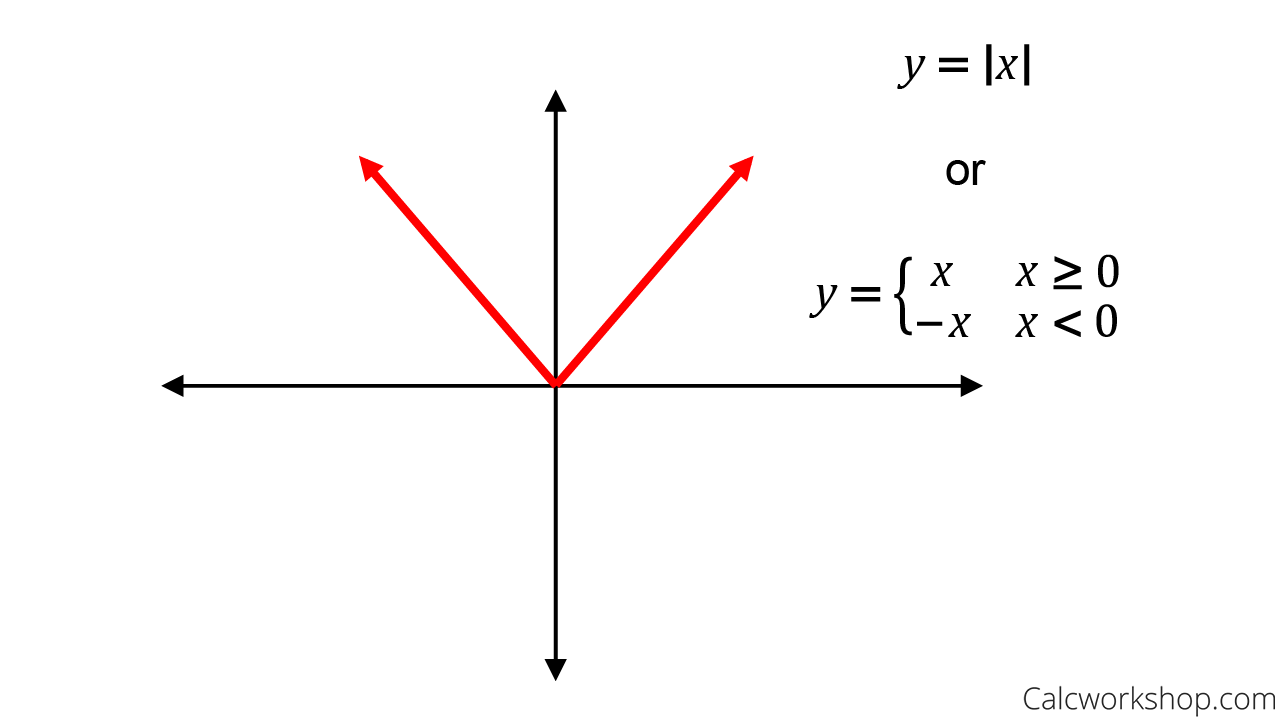
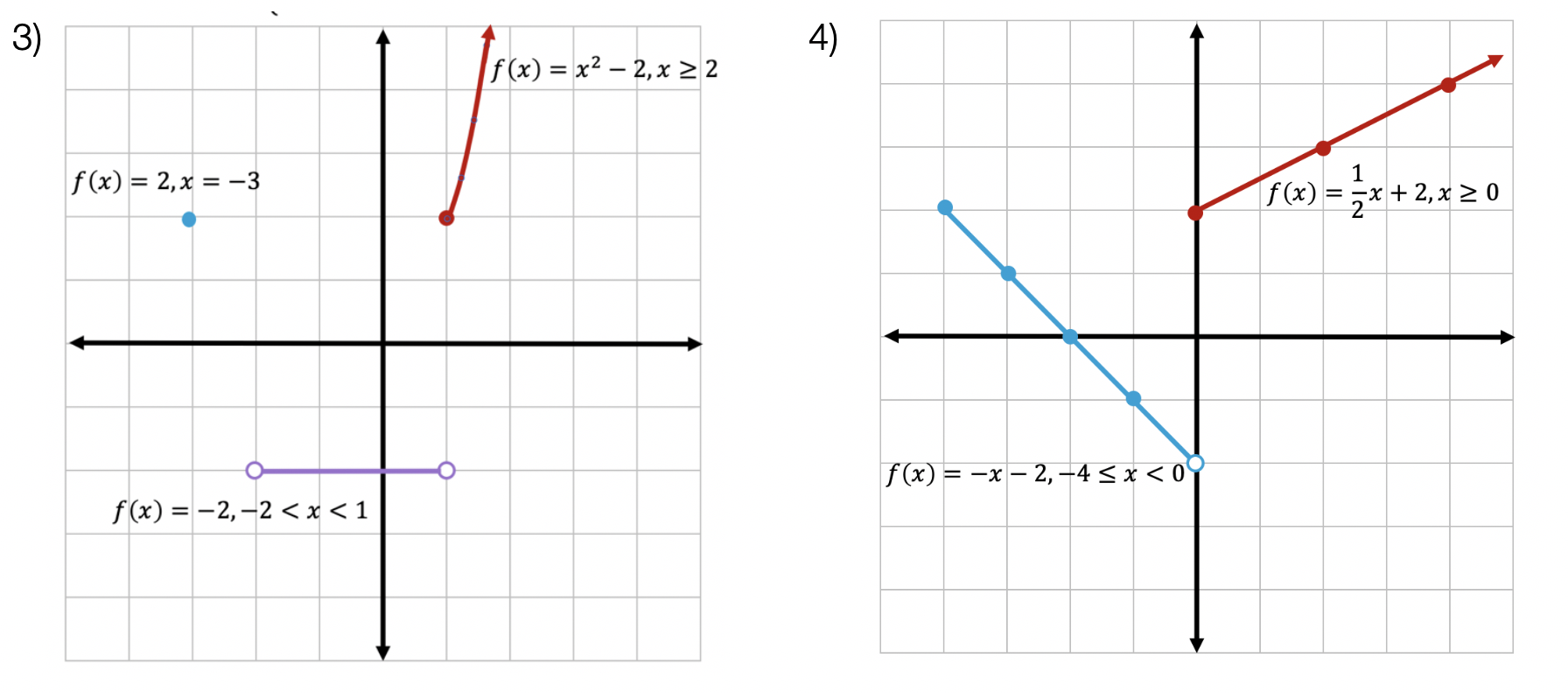
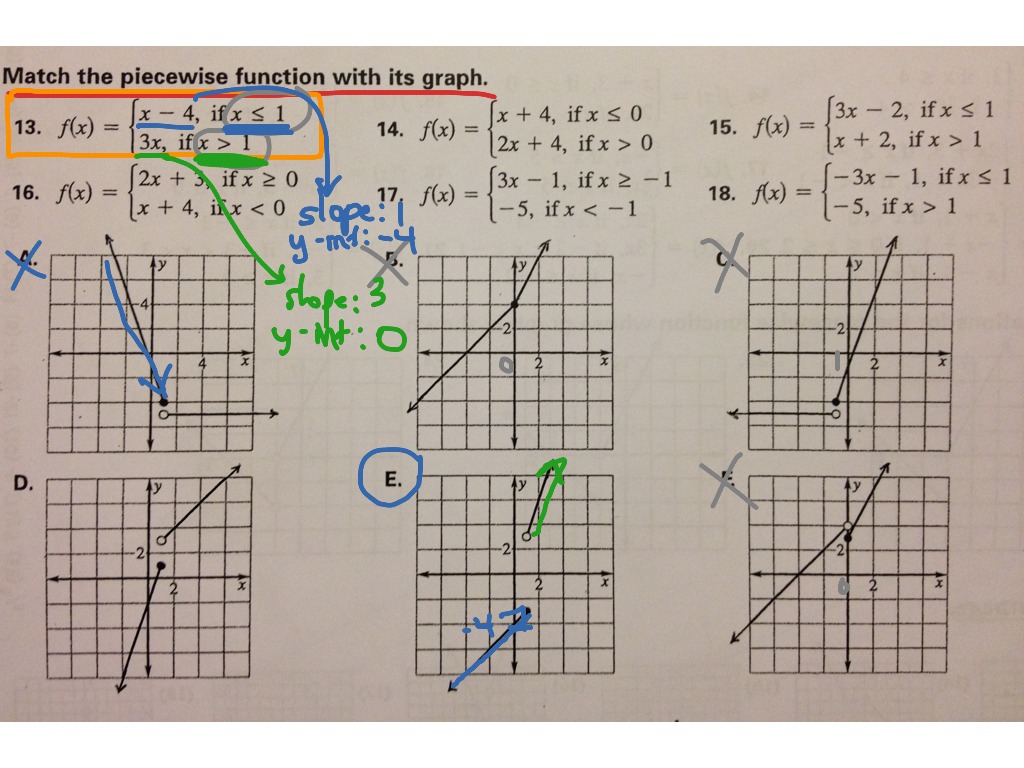
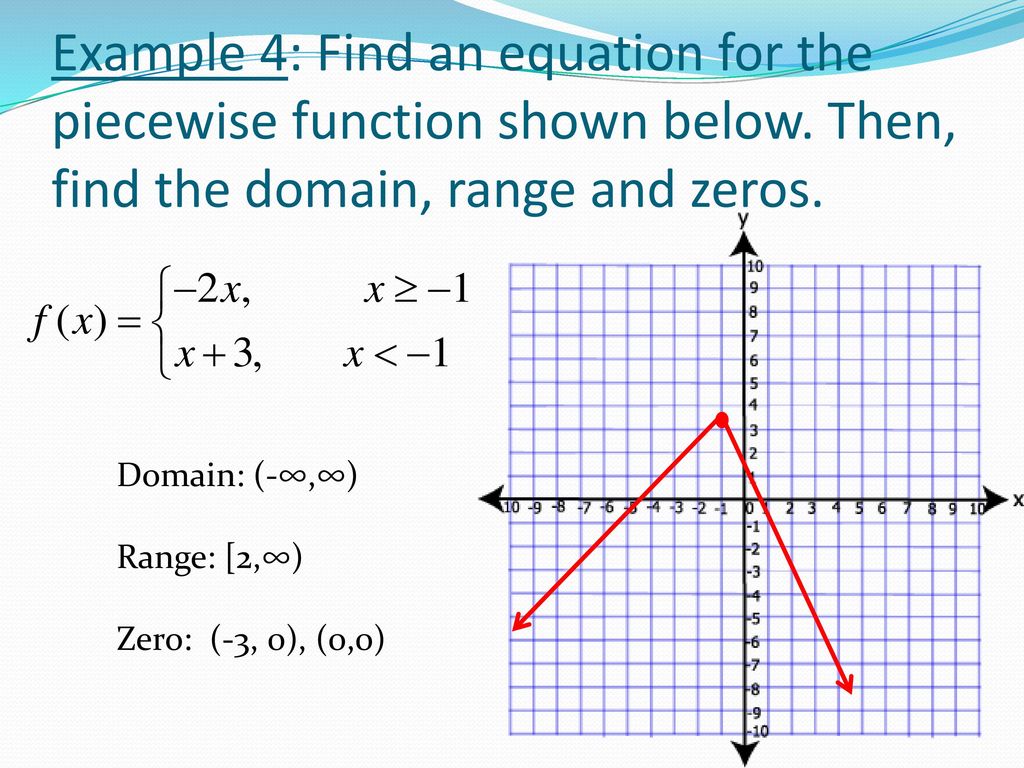
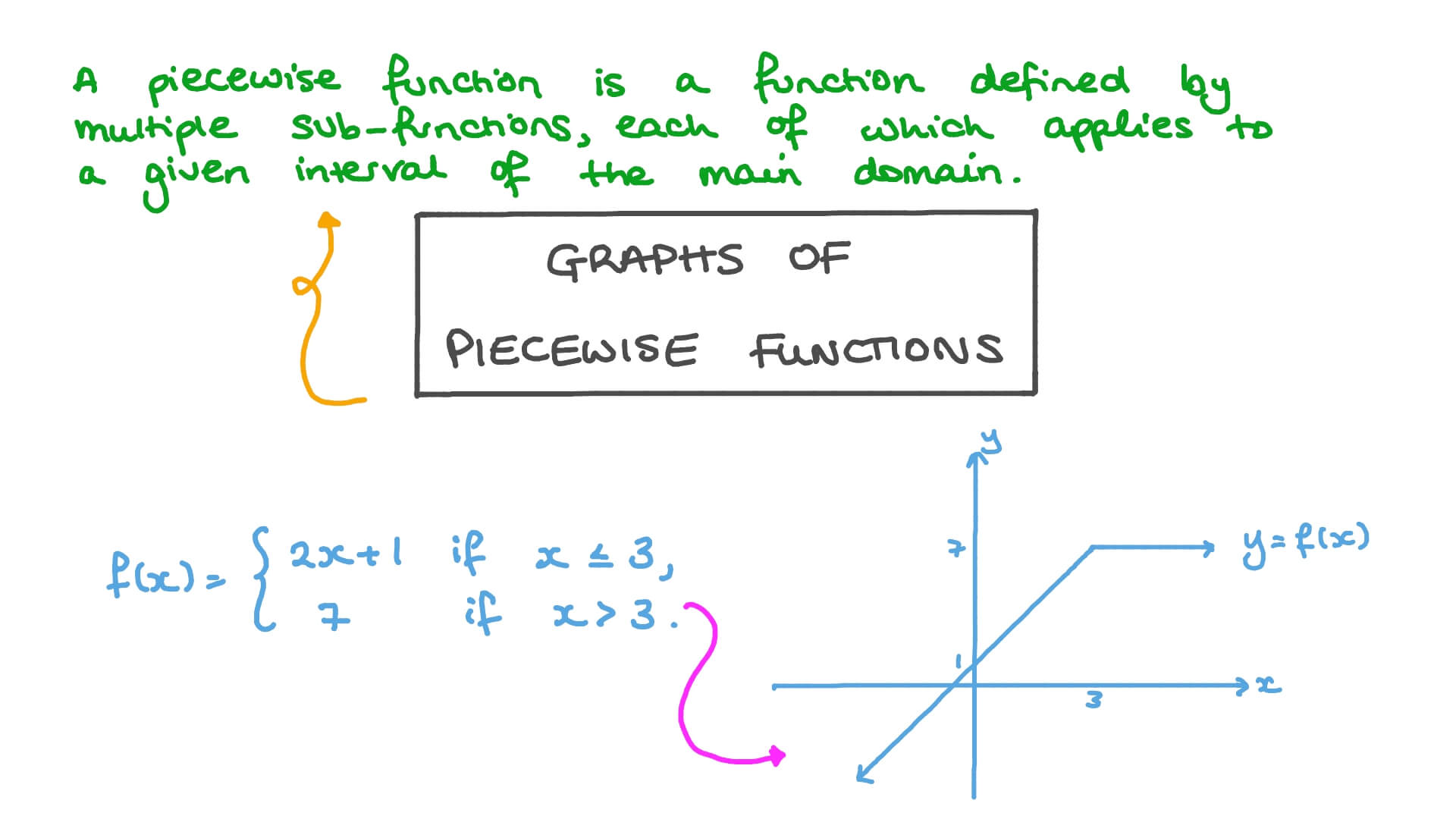
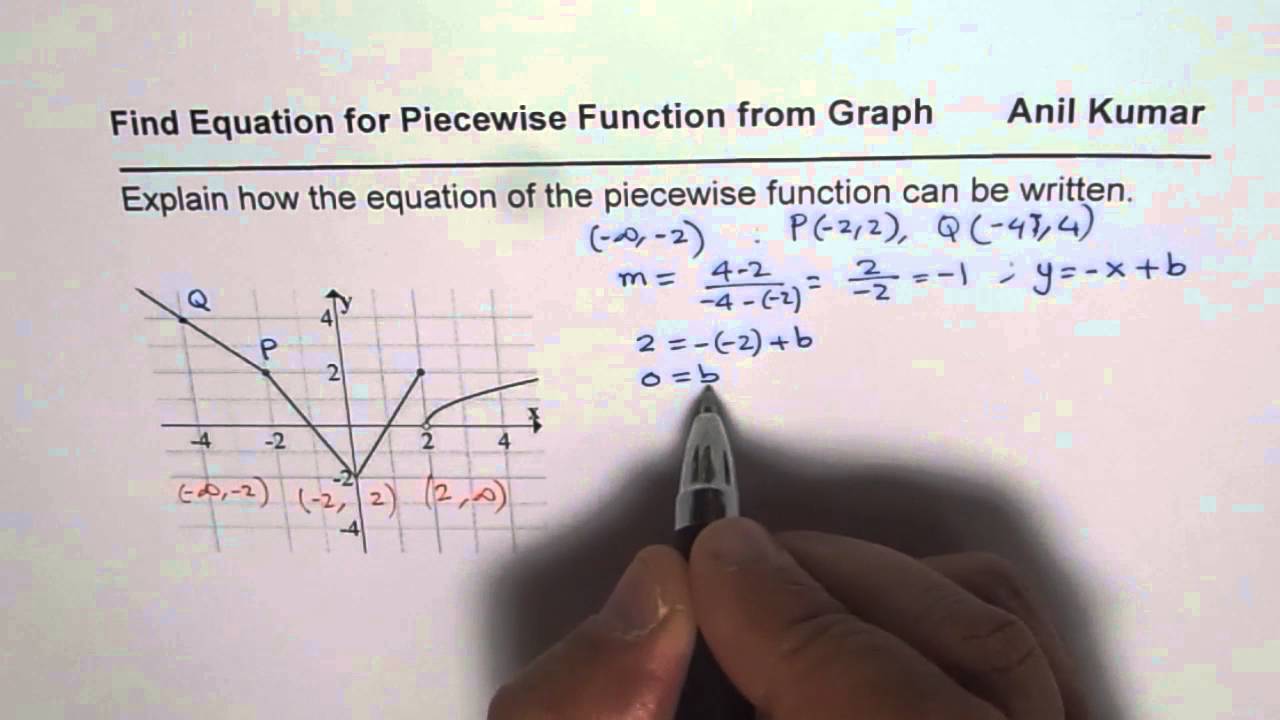
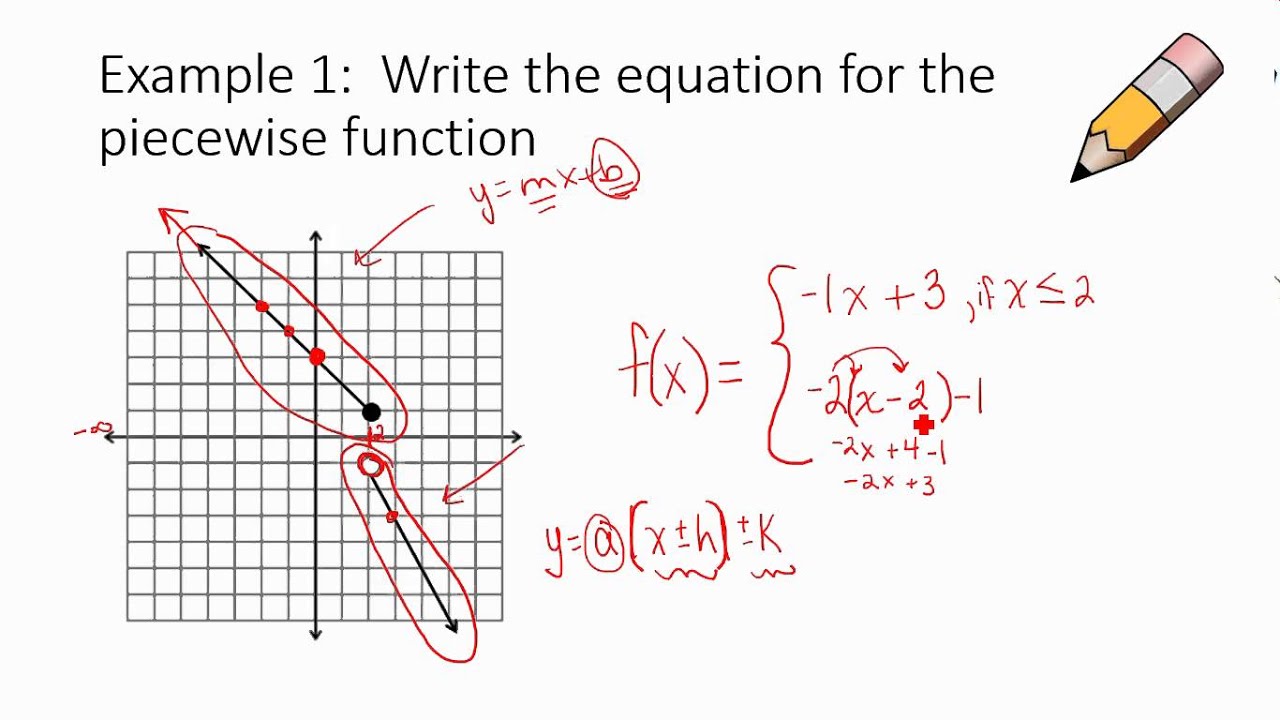
How To Write Piecewise Function Equations – How To Write Piecewise Function Equations
| Allowed in order to our weblog, in this moment I’ll show you regarding How To Clean Ruggable. And after this, here is the first impression:
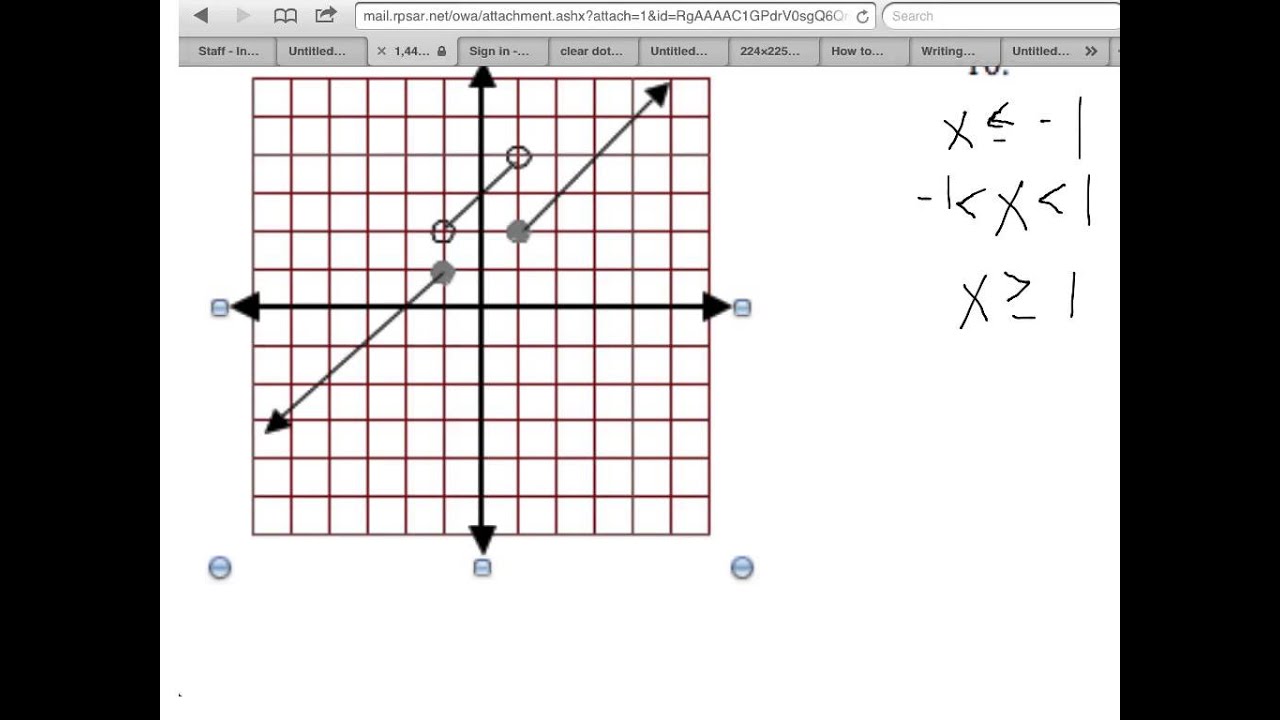
Why don’t you consider picture earlier mentioned? is which amazing???. if you think maybe consequently, I’l l teach you several image all over again under:
So, if you desire to receive these magnificent images about (How To Write Piecewise Function Equations), press save button to save these images in your personal pc. There’re prepared for transfer, if you want and wish to get it, click save logo on the web page, and it will be immediately downloaded in your laptop.} At last if you would like find new and recent graphic related with (How To Write Piecewise Function Equations), please follow us on google plus or bookmark this blog, we attempt our best to give you regular up grade with all new and fresh pictures. Hope you like keeping right here. For many updates and latest information about (How To Write Piecewise Function Equations) graphics, please kindly follow us on tweets, path, Instagram and google plus, or you mark this page on book mark section, We try to present you up-date periodically with fresh and new shots, like your surfing, and find the best for you.
Thanks for visiting our website, contentabove (How To Write Piecewise Function Equations) published . Nowadays we’re excited to declare we have discovered an extremelyinteresting nicheto be reviewed, namely (How To Write Piecewise Function Equations) Many individuals searching for info about(How To Write Piecewise Function Equations) and of course one of them is you, is not it?