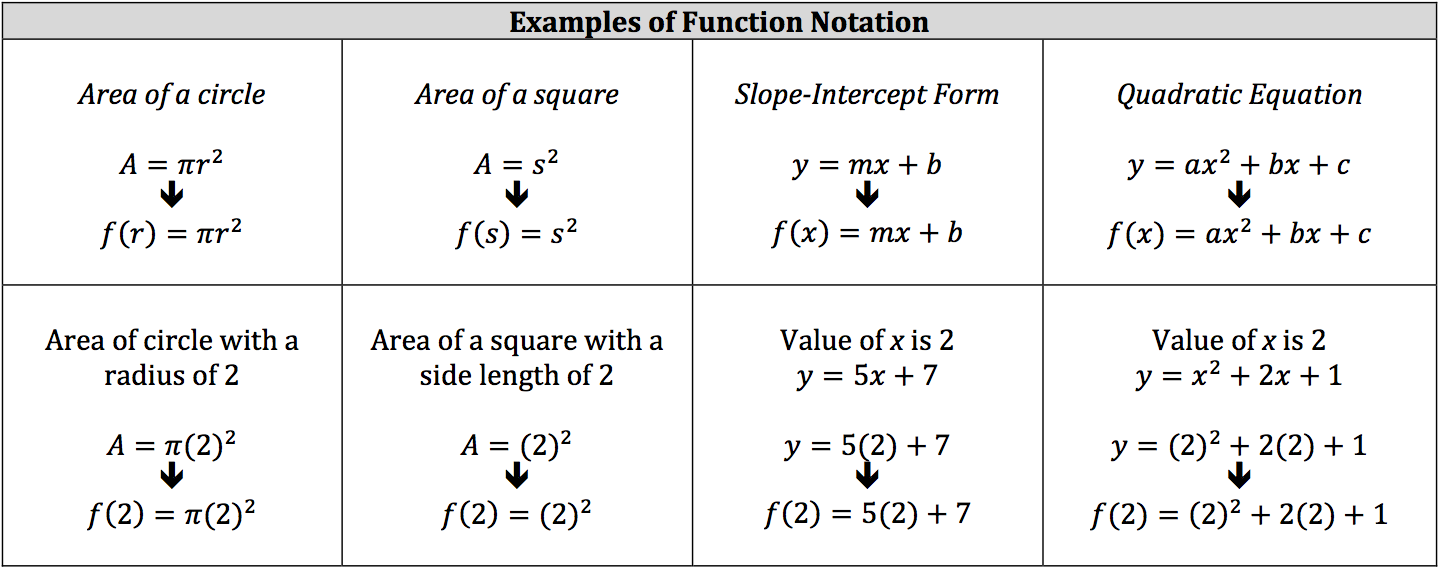
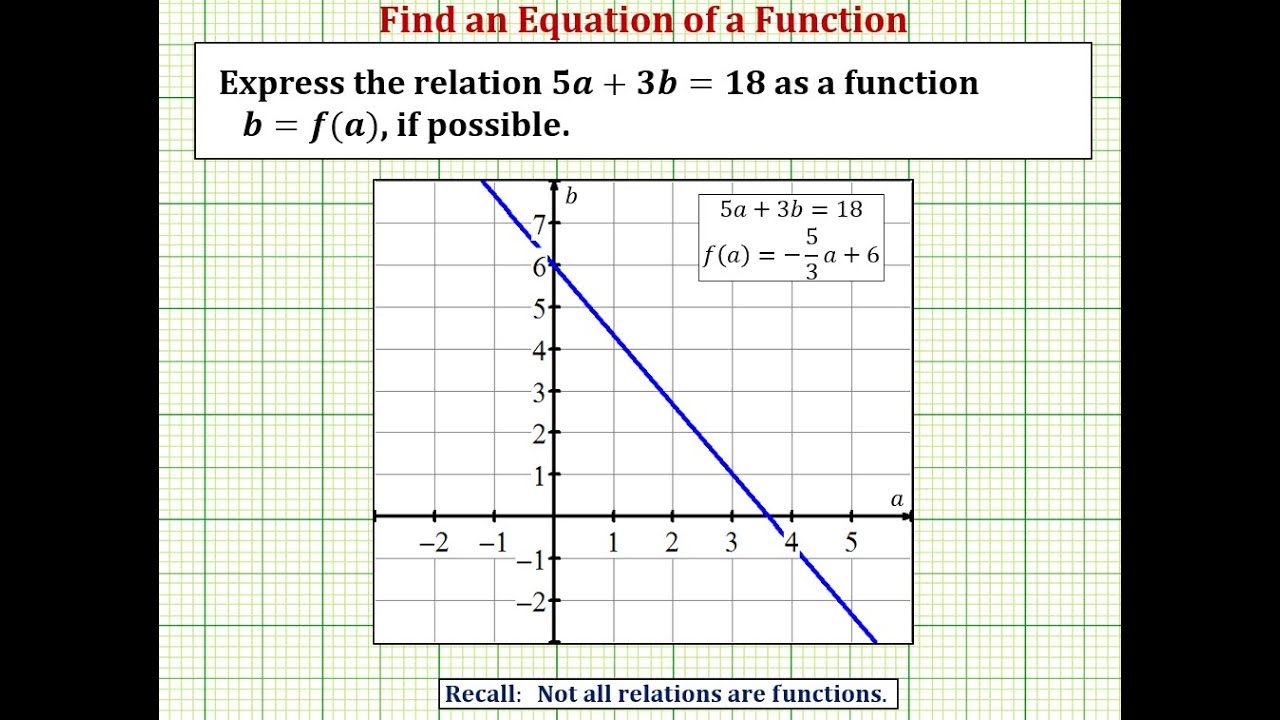
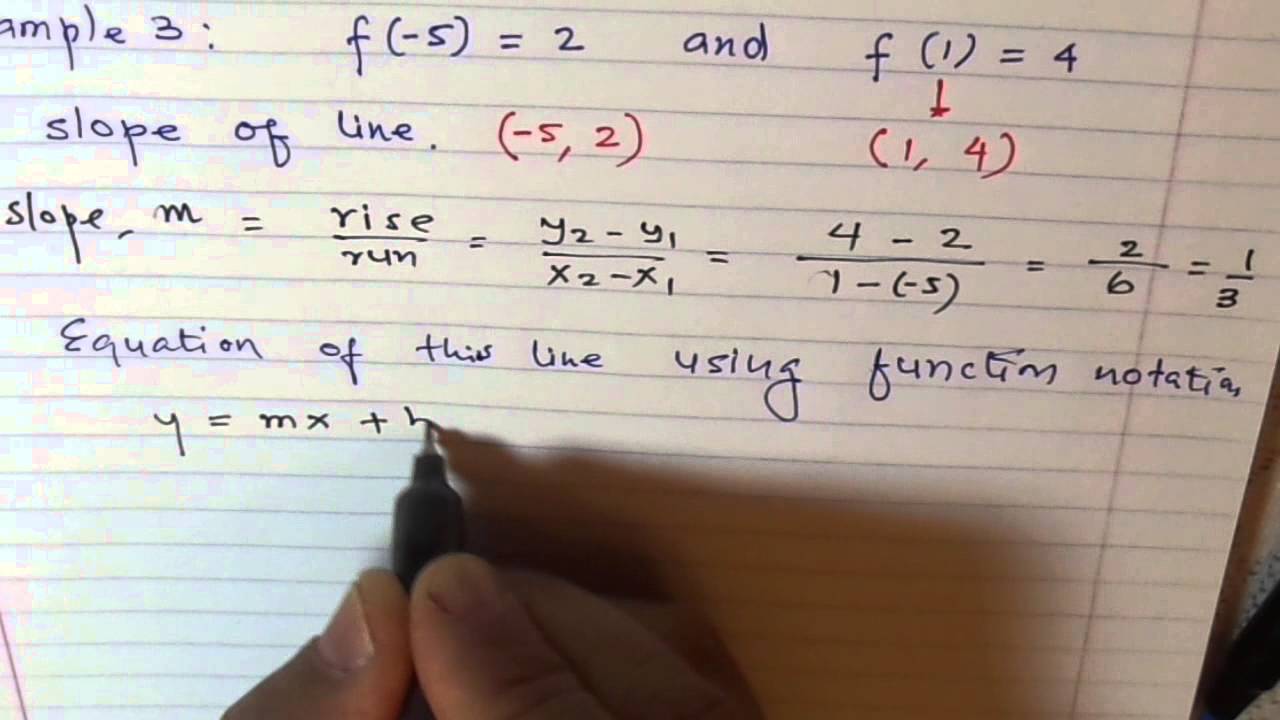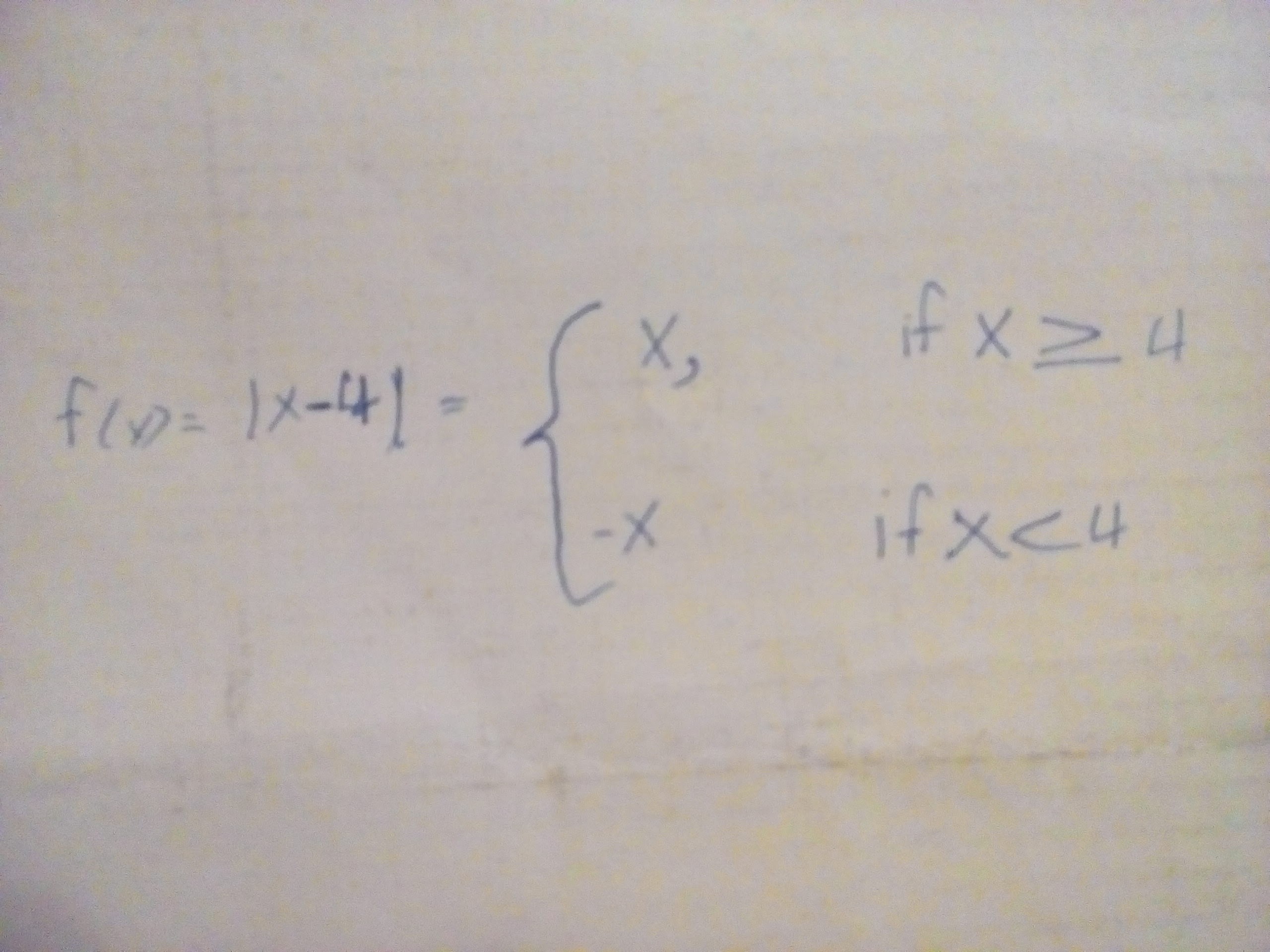A action links an ascribe amount to an achievement value. Functions are accounting in action characters with the name of the action (usually (f) or (g)), a capricious accounting in brackets and an expression. Aback artful the amount of a function, the ascribe amount is commissioned into the expression.

(f(x) = 3x 2) and (g(x) = x^2 – 1)
[f(-2) = 3 times -2 2 = -4]
[g(3) = 3 times 3 – 1 = 8]
Composite functions are fabricated aback the achievement from one action is acclimated as the ascribe of addition function. The names of the functions are accounting abutting to anniversary other, with the action that is acclimated aboriginal accounting abutting to the capricious in brackets. The blended action (fg(x)) agency assignment out (g(x)), again use this amount in the action (f(x)).
(f(x) = 2x 3) and (g(x) = x^2)
Find (fg(4)), (gf(4)) and (ff(4))
(fg(4)) agency assignment out (g(4)), again assignment out (f(x)) for this value.
[g(4) = 42 = 16]
So(fg(4) = f(16) = 2 times 16 3 = 35)
(gf(4)) agency assignment out (f(4)), again assignment out (g(x)) for this value.
[f(4) = 2 times 4 3 = 11]
So (gf(4) = g(11) = 11^2 = 121)
(ff(4)) agency assignment out (f(4)), again assignment out (f(x)) for this value.

[f(4) = 2 times 4 3 = 11]
So (ff(4) = f(11) = 2 times 11 3 = 25)
A action links an ascribe amount to an achievement value. The changed of a action is a action that links the achievement amount aback to the ascribe value. The changed action for (f(x)) is accounting as (f^{-1}(x)).
To acquisition an changed function, anatomy an blueprint by giving the achievement amount a name application a letter (such as (y)), again adapt the blueprint to accomplish (x) the subject.
[f(x) = 5x -4]
Find (f^{-1}(x))
Form an blueprint by authoritative (y=f(x) ): (y=5x-4)

Make (x) the subject. First, add 4 to both abandon of the equation:
[y 4=5x]
Then bisect both abandon by 5:
[frac {y 4}{5} = x]
Finally, re-write the announcement that is according to (x), replacing the (y) with an (x):
The changed action of (f(x) = 5x 4) is: (f(x) = frac{x 4}{5})
You can analysis your acknowledgment by seeing if (f^{-1}(x)) does about-face (f(x)). For example, (f(2) = 10 – 4 = 6 ) and (f^{-1}(6) = frac{6 4}{5} = 2).

How To Write An Equation In Function Notation – How To Write An Equation In Function Notation
| Encouraged to be able to the blog site, within this period I will demonstrate with regards to How To Factory Reset Dell Laptop. And after this, this can be a initial picture:

Why not consider graphic earlier mentioned? can be that awesome???. if you think and so, I’l m teach you a few graphic once more beneath:
So, if you desire to get these awesome pics related to (How To Write An Equation In Function Notation), click save icon to save the pictures in your laptop. They are all set for transfer, if you want and wish to get it, just click save logo on the article, and it’ll be immediately downloaded in your pc.} Finally if you want to grab unique and latest graphic related to (How To Write An Equation In Function Notation), please follow us on google plus or bookmark this page, we attempt our best to present you daily up grade with all new and fresh images. We do hope you love staying here. For most updates and recent news about (How To Write An Equation In Function Notation) pics, please kindly follow us on tweets, path, Instagram and google plus, or you mark this page on bookmark area, We attempt to present you update periodically with fresh and new pictures, like your exploring, and find the perfect for you.
Here you are at our website, contentabove (How To Write An Equation In Function Notation) published . Today we’re pleased to declare we have found a veryinteresting topicto be discussed, namely (How To Write An Equation In Function Notation) Many individuals searching for information about(How To Write An Equation In Function Notation) and of course one of these is you, is not it?